Article contents
Remarks on the Elliptic Case of the Mapping Theorem for Simply-Connected Riemann Surfaces
Published online by Cambridge University Press: 22 January 2016
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
It is well-known that the conformal equivalence of a compact simply-connected Riemann surface to the extended plane is readily established once it is shown that given a local uniformizer t(p) which carries a given point p 0 of the surface into 0, there exists a function u harmonic on the surface save at p 0 which admits near p 0 a representation of the form

(α complex 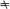 0; h harmonic at p 0). For the monodromy theorem then implies the existence of a meromorphic function on the surface whose real part is u. Such a meromorphic function has a simple pole at p 0 and elsewhere is analytic. It defines a univalent conformal map of the surface onto the extended plane.
0; h harmonic at p 0). For the monodromy theorem then implies the existence of a meromorphic function on the surface whose real part is u. Such a meromorphic function has a simple pole at p 0 and elsewhere is analytic. It defines a univalent conformal map of the surface onto the extended plane.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1955
- 1
- Cited by

