Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gebuhrer, Marc Olivier
1991.
Probability Measures on Groups X.
p.
145.
1995.
Harmonic Analysis of Probability Measures on Hypergroups.
p.
553.

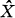 denote the dual group of
denote the dual group of 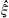 the Haar measure associated with
the Haar measure associated with 