Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-04T23:02:23.075Z Has data issue: false hasContentIssue false
  • English
  • Français

Remarks to the Paper “On Montel’s Theorem’ By Kawakami

Published online by Cambridge University Press:  22 January 2016

Makoto Ohtsuka
Makoto Ohtsuka*
Affiliation:
Mathematical Institute Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We take a measurable set E on the positive η-axis and denote by μ(r) the linear measure of the part of E in the interval 0 < η < r. The lower density of E at η = 0 is defined by

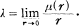
Theorem by Kawakami [1] asserts that if λ is positive, if a function f(ζ) = f(ξ + iη) is bounded analytic in ξ > 0 and continuous at E, and if f(ζ) → A as ζ → 0 along E, then f(ζ) → A as ζ → 0 in ∣η∣ ≦ kξ for any k > 0.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 10 , June 1956 , pp. 165 - 169
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1956

References

[ 1 ] Kawakami, Y.: On Montel’s theorem, Nagoya Math. J., 10 (1956), pp. 125–127.Google Scholar
[ 2 ] Ohtsuka, M. : Generalizations of Montel-Lindelöf’s theorem on asymptotic values, ibid., pp. 129–163.Google Scholar