Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T19:23:02.415Z Has data issue: false hasContentIssue false
  • English
  • Français

REPETITIVE EQUIVALENCES AND TILTING THEORY

Part of: Abelian categories General theory of categories and functors Homological methods Modules, bimodules and ideals

Published online by Cambridge University Press:  06 December 2019

JIAQUN WEI
JIAQUN WEI*
Affiliation:
Department of Mathematics, Northwest Normal University, Lanzhou730070, China Institution of Mathematics, School of Mathematics Science, Nanjing Normal University, Nanjing210023, China email weijiaqun@njnu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 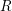$R$ be a ring and 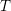$T$ be a good Wakamatsu-tilting module with 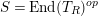$S=\text{End}(T_{R})^{op}$. We prove that $T$ induces an equivalence between stable repetitive categories of 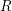$R$ and 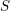$S$ (i.e., stable module categories of repetitive algebras 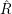$\hat{R}$ and 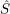${\hat{S}}$). This shows that good Wakamatsu-tilting modules seem to behave in Morita theory of stable repetitive categories as that tilting modules of finite projective dimension behave in Morita theory of derived categories.

MSC classification

Primary: 18E10: Exact categories, abelian categories 16D90: Module categories ; module theory in a category-theoretic context; Morita equivalence and duality 16E05: Syzygies, resolutions, complexes 16D20: Bimodules 18A25: Functor categories, comma categories 16E99: None of the above, but in this section
Type
Article
Information
Nagoya Mathematical Journal , Volume 243 , September 2021 , pp. 97 - 136
Check for updates
Copyright
© 2019 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author is supported by the Natural Science Foundation of China (Grant No. 11771212) and a project funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.

References

Angeleri-Hügel, L. and Coelho, F.U., Infinitely generated tilting modules of finite projective dimension, Forum Math. 13 (2001), 239–250.Google Scholar
Asashiba, H., A covering technique for derived equivalence, J. Algebra 191 (1997), 382–415.10.1006/jabr.1997.6906CrossRefGoogle Scholar
Auslander, M. and Reiten, I., Applications of contravariantly finite subcategories, Adv. Math. 86 (1991), 111–152.CrossRefGoogle Scholar
Bazzoni, S., A characterization of n-cotilting and n-tilting modules, J. Algebra 273(1) (2004), 359–372.CrossRefGoogle Scholar
Bongartz, K., “Tilted algebras”, in Representations of Algebras, Lecture Notes in Mathematics 903, Springer-Verlag, Berlin/Heidelberg/New York, 1981, 26–38.CrossRefGoogle Scholar
Brenner, S. and Butler, M. C. R., Generalizations of the Bernstein–Gelfand–Ponomarev Reflection Functors, Lecture Notes in Mathematics 832, 1980, 103–170.Google Scholar
Chen, Q., Derived equivalence of repetitive algebras, Adv. Math. (Chinese) 37(2) (2008), 189–196.Google Scholar
Chen, X., The singularity category of an algebra with radical square zero, Doc. Math. 16 (2011), 921–936.Google Scholar
Chen, X. and Wei, J., Wakamatsu’s equivalence revisited, arXiv:1610.09649.Google Scholar
Cline, E., Parshall, B. and Scott, L., Derived categories and Morita theory, J. Algebra 104 (1986), 397–409.CrossRefGoogle Scholar
Colby, R. and Fuller, K. R., Tilting and torsion theory counter equivalences, Comm. Algebra 23(13) (1995), 4833–4849.CrossRefGoogle Scholar
Colby, R. and Fuller, K. R., Tilting, cotilting and serially tilted rings, Comm. Algebra 25(10) (1997), 3225–3237.Google Scholar
Colpi, R., D’Este, G. and Tonolo, A., Quasi-tilting modules and counter equivalences, J. Algebra 191 (1997), 461–494.10.1006/jabr.1997.6873CrossRefGoogle Scholar
Colpi, R. and Trlifaj, J., Tilting modules and tilting torsion theories, J. Algebra 178 (1995), 614–634.10.1006/jabr.1995.1368CrossRefGoogle Scholar
Enochs, E. E. and Jenda, O. M. G., Relative Homological Algebra, De Gruyter Expositions in Mathematics 30, Walter De Gruyter, Berlin/New York, 2000.10.1515/9783110803662CrossRefGoogle Scholar
Göbel, R. and Trlifaj, J., Approximations and Endomorphism Algebras of Modules, De Gruyter Expositions in Mathematics 41, Walter de Gruyter, Berlin/New York, 2012.CrossRefGoogle Scholar
Green, E. L., Reiten, I. and Solberg, Ø., Dualities on Generalized Koszul Algebras, Mem. Amer. Math. Soc. 159 (2002), xvi+67 pp.Google Scholar
Happel, D., Triangulated Categories in the Representation Theory of Finite Dimension Algebras, London Mathematical Society Lecture Notes Series 119, Cambridge University Press, Cambridge, 1988.CrossRefGoogle Scholar
Happel, D. and Ringel, C. M., Tilted algebras, Trans. Amer. Math. Soc. 174 (1982), 399–443.CrossRefGoogle Scholar
Hughes, D. and Waschbüsch, J., Trivial extensions of tilted algebras, Proc. Lond. Math. Soc. 46 (1983), 347–364.10.1112/plms/s3-46.2.347CrossRefGoogle Scholar
Keller, B., Deriving DG categories, Ann. Sci. Éc. Norm. Supér. 27 (1994), 63–102.10.24033/asens.1689CrossRefGoogle Scholar
Mantese, F. and Reiten, I., Wakamatsu Tilting modules, J. Algebra 278 (2004), 532–552.CrossRefGoogle Scholar
Miyashita, Y., Tilting modules of finite projective dimension, Math. Z. 193 (1986), 113–146.10.1007/BF01163359CrossRefGoogle Scholar
Rickard, J., Morita theory for derived categories, J. Lond. Math. Soc. 39 (1989), 436–456.CrossRefGoogle Scholar
Wakamatsu, T., On modules with trivial self-extensions, J. Algebra 114 (1988), 106–114.10.1016/0021-8693(88)90215-3CrossRefGoogle Scholar
Wakamatsu, T., Stable equivalence for self-injective algebras and a generalization of tilting modules, J. Algebra 134 (1990), 298–325.10.1016/0021-8693(90)90055-SCrossRefGoogle Scholar
Wakamatsu, T., On constructing stable equivalent functor, J. Algebra 148 (1992), 277–288.10.1016/0021-8693(92)90193-PCrossRefGoogle Scholar
Yamaura, K., Realizing stable categories as derived categories, Adv. Math. 248 (2013), 784–819.CrossRefGoogle Scholar
Yoshino, Y., “Modules of G-dimension zero over local rings with the cube of maximal ideal being zero”, in Commutative Algebra, Singularities and Computer Algebra, NATO Sci. Ser. I Math. Phys. Chem. 115, Kluwer, Dordrecht, 2003, 255–273.CrossRefGoogle Scholar