Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T09:01:51.821Z Has data issue: false hasContentIssue false
  • English
  • Français

Riesz capacity and regular boundary points for the parabolic operator of order α

Published online by Cambridge University Press:  22 January 2016

Masaharu Nishio
Masaharu Nishio*
Affiliation:
Department of Mathematics, Osaka City University, Sugimoto, Sumiyoshi Osaka 558, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Rn+1 = Rn × R be the (n + 1)-dimensional Euclidean space with n ≥ 1. We denote by X = (x, t) a point in Rn+1 with x ∈ Rn and t ∈ R. Consider the parabolic operator on Rn+1:

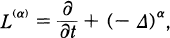
where 0 < a ≤ 1 and Δ denotes the Laplacian on Rn.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 139 , September 1995 , pp. 185 - 196
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1995

References

[EF] Effros, E. and Kazdan, J., On the Dirichlet problem for the heat equation, Indiana Univ. Math. J., 20 (1971), 683–693.CrossRefGoogle Scholar
[EG] Evans, L. and Gariepy, R., Wiener’s criterion for the heat equation, Arch. Rational Mech. Anal, 78 (1982), 293–314.Google Scholar
[IN] Itô, M. and Nishio, M., Poincaré type conditions of the regularity for the parabolic operator of order a , Nagoya Math. J., 115 (1989), 1–22.Google Scholar
[N] Nishio, M., The Wiener criterion of regular points for the parabolic operator of order a, Nagoya Math. J., 116 (1989), 163–179.Google Scholar
[W] Watson, N. A., Thermal capacity, Proc. London Math. Soc, 37 (1978), 342–362.CrossRefGoogle Scholar