Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T07:00:05.423Z Has data issue: false hasContentIssue false
  • English
  • Français

Rigidity of Linear Strands and Generic Initial Ideals

Published online by Cambridge University Press:  11 January 2016

Satoshi Murai  and
Pooja Singla
Satoshi Murai
Affiliation:
Department of Pure and Applied Mathematics, Graduate School of Information Science and Technology, Osaka University, Toyonaka, Osaka, 560-0043, Japan, s-murai@ist.osaka-u.ac.jp
Pooja Singla
Affiliation:
FB Mathematik, Universität Duisburg-Essen, Campus Essen, 45117 Essen, Germany, pooja.singla@uni-duisburg-essen.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let K be a field, S a polynomial ring and E an exterior algebra over K, both in a finite set of variables. We study rigidity properties of the graded Betti numbers of graded ideals in S and E when passing to their generic initial ideals. First, we prove that if the graded Betti numbers 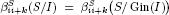for some i > 1 and k ≥ 0, then 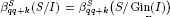for all q ≥ i, where I ⊂ S is a graded ideal. Second, we show that if 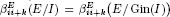for some i > 1 and k ≥ 0, then 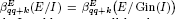for all q ≥ 1, where I ⊂ E is a graded ideal. In addition, it will be shown that the graded Betti numbers 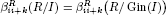for all i ≥ 1 if and only if I(k) and I(k+1) have a linear resolution. Here I(d) is the ideal generated by all homogeneous elements in I of degree d, and R can be either the polynomial ring or the exterior algebra.

Keywords

13D02
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 190 , 2008 , pp. 35 - 61
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2008

References

[1] Aramova, A. and Herzog, J., Almost regular sequences and Betti numbers, Amer. J. Math., 122 (2000), 689–719.Google Scholar
[2] Aramova, A., Herzog, J. and Hibi, T., Gotzmann theorems for exterior algebras and combinatorics, J. Alg., 191 (1997), 174–211.CrossRefGoogle Scholar
[3] Aramova, A., Herzog, J. and Hibi, T., Squarefree lexsegment ideals, Math. Z., 228 (1998), 353–378.CrossRefGoogle Scholar
[4] Aramova, A., Herzog, J. and Hibi, T., Ideals with stable Betti numbers, Adv. Math., 152 (2000), no. 1, 72–77.CrossRefGoogle Scholar
[5] Bayer, D. and Stillman, M., A criterion for detecting m-regularity, Invent. Math., 87 (1987), 1–11.CrossRefGoogle Scholar
[6] Bruns, W. and Herzog, J., Cohen-Macaulay rings, Revised Edition, Cambridge University Press, Cambridge, 1996.Google Scholar
[7] Bigatti, A. M., Upper bound for the Betti numbers of a given Hilbert function, Comm. in Alg., 21 (1993), 2317–2334.Google Scholar
[8] CoCoA Team, CoCoA: a system for doing Computations in Commutative Algebra, available at http://cocoa.dima.unige.it.Google Scholar
[9] Conca, A., Koszul homology and extremal property of Gin and Lex, Trans. Amer. Math. Soc., 256 (2004), no. 7, 2945–2961.Google Scholar
[10] Conca, A., Herzog, J. and Hibi, T., Rigid resolutions and big Betti numbers, Comment. Math. Helv., 79 (2004), 826–839.CrossRefGoogle Scholar
[11] Eisenbud, D., Commutative Algebra with a View Toward Algebraic Geometry, Graduate Texts in Math., Springer-Verlag: New-York, 1995.Google Scholar
[12] Eliahou, S. and Kervaire, M., Minimal resolutions of some monomial ideals, J. of Algebra, 129 (1990), 1–25.Google Scholar
[13] Green, M., Generic initial ideals, Six Lectures on Commutative Algebra (J. Elias, J. M. Giral, R. M. Miró-Roig, and S. Zarzuela, eds.), Progress in Math., 166, Birkhäuser, Basel, 1998, pp. 119–186.Google Scholar
[14] Herzog, J., Generic initial ideals and graded Betti numbers, Computational Commutative Algebra and Combinatorics (T. Hibi, ed.), Advanced Studies in Pure Math., Volume 33, 2002, pp. 75–120.Google Scholar
[15] Herzog, J. and Hibi, T., Componentwise linear ideals, Nagoya Math. J., 153 (1999), 141–153.Google Scholar
[16] Murai, S. and Hibi, T., Gin, and Lex, of certain monomial ideals, Math. Scand., 99 (2006), no. 1, 76–86.Google Scholar
[17] Kodiyalam, V., Homological Invariants of Powers of an Ideal, Proc. Amer. Math. Soc., 118 (1993), no. 3, 757–763.Google Scholar
[18] Kodiyalam, V., Asymptotic Behavior of Castelnuovo-Mumford Regularity, Proc. Amer. Math. Soc., 128 (1999), no. 2, 407–411.Google Scholar
[19] Nagel, U., Römer, T. and Vinai, N. P., Algebraic shifting and exterior and symmetric algebra methods, Comm. Algebra, 36 (2008), no. 1, 208–231.Google Scholar