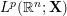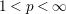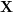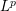1 Introduction
Let
![]() $\mathbf{X}$
be a Banach space,
$\mathbf{X}$
be a Banach space,
![]() $\unicode[STIX]{x1D6E4}:\mathbb{R}^{k}\rightarrow \mathbb{R}^{n}$
be a
$\unicode[STIX]{x1D6E4}:\mathbb{R}^{k}\rightarrow \mathbb{R}^{n}$
be a
![]() $C^{\infty }$
mapping. Let
$C^{\infty }$
mapping. Let
![]() $K$
be a Calderón–Zygmund kernel in
$K$
be a Calderón–Zygmund kernel in
![]() $\mathbb{R}^{k}$
, that is,
$\mathbb{R}^{k}$
, that is,
![]() $K$
is homogeneous of degree
$K$
is homogeneous of degree
![]() $-k$
, smooth away from the origin, and
$-k$
, smooth away from the origin, and
To
![]() $\unicode[STIX]{x1D6E4}$
we associate vector-valued singular integrals
$\unicode[STIX]{x1D6E4}$
we associate vector-valued singular integrals
![]() $T_{\unicode[STIX]{x1D6E4}}$
defined for
$T_{\unicode[STIX]{x1D6E4}}$
defined for
![]() $f\in \mathscr{S}(\mathbb{R}^{n};\mathbf{X})$
as follows:
$f\in \mathscr{S}(\mathbb{R}^{n};\mathbf{X})$
as follows:
In addition to the classical case
![]() $n=k$
and
$n=k$
and
![]() $\unicode[STIX]{x1D6E4}(t)=(t_{1},t_{2},\ldots ,t_{n})$
, much effort has been devoted to the question of whether the mapping properties of singular integral operators could be extended to the Lebesgue–Bôhner spaces
$\unicode[STIX]{x1D6E4}(t)=(t_{1},t_{2},\ldots ,t_{n})$
, much effort has been devoted to the question of whether the mapping properties of singular integral operators could be extended to the Lebesgue–Bôhner spaces
![]() $L^{p}(\mathbb{R}^{n};\mathbf{X})$
(
$L^{p}(\mathbb{R}^{n};\mathbf{X})$
(
![]() $1<p<\infty$
) of vector-valued functions. In [Reference Benedek, Caldern and Panzone1], Benedek et al. proved that the boundedness on
$1<p<\infty$
) of vector-valued functions. In [Reference Benedek, Caldern and Panzone1], Benedek et al. proved that the boundedness on
![]() $L^{p_{0}}(\mathbb{R}^{n};\mathbf{X})$
for one
$L^{p_{0}}(\mathbb{R}^{n};\mathbf{X})$
for one
![]() $1<p_{0}<\infty$
of a singular integral operator, together with Hörmander’s condition, implies its boundedness on
$1<p_{0}<\infty$
of a singular integral operator, together with Hörmander’s condition, implies its boundedness on
![]() $L^{p}(\mathbb{R}^{n};\mathbf{X})$
for all
$L^{p}(\mathbb{R}^{n};\mathbf{X})$
for all
![]() $1<p<\infty$
. But, it is significantly difficult to get the
$1<p<\infty$
. But, it is significantly difficult to get the
![]() $L^{p_{0}}(\mathbb{R}^{n};\mathbf{X})$
-boundedness except in the case
$L^{p_{0}}(\mathbb{R}^{n};\mathbf{X})$
-boundedness except in the case
![]() $\mathbf{X}=L^{p_{0}}(\unicode[STIX]{x1D6FA})$
for some measure space
$\mathbf{X}=L^{p_{0}}(\unicode[STIX]{x1D6FA})$
for some measure space
![]() $\unicode[STIX]{x1D6FA}$
. In this direction, Burkholder [Reference Burkholder4] showed that if the underlying Banach space
$\unicode[STIX]{x1D6FA}$
. In this direction, Burkholder [Reference Burkholder4] showed that if the underlying Banach space
![]() $\mathbf{X}$
satisfies the so-called UMD-property, that is,
$\mathbf{X}$
satisfies the so-called UMD-property, that is,
![]() $\mathbf{X}$
is an UMD space, then the Hilbert transform is bounded on
$\mathbf{X}$
is an UMD space, then the Hilbert transform is bounded on
![]() $L^{p}(\mathbb{R};\mathbf{X})$
for any
$L^{p}(\mathbb{R};\mathbf{X})$
for any
![]() $1<p<\infty$
. Moreover, the UMD-property was shown by Bourgain [Reference Bourgain3] to be necessary for the boundedness of the Hilbert transform. The analogue statement also holds for Riesz transforms, which can be found in [Reference Rubio de Francia, Ruiz and Torrea12]. It is well known that Riesz transforms are prototypes of singular integral operators and Fourier multipliers, their boundedness motivates McConnell’s [Reference McConnell9] and Zimmermann’s [Reference Zimmermann19] results on vector-valued Marcinkiewicz–Mihlin multipliers, and motivates Hytönen and Weis’s [Reference Hytönen and Weis6] results on vector-valued singular convolution integrals.
$1<p<\infty$
. Moreover, the UMD-property was shown by Bourgain [Reference Bourgain3] to be necessary for the boundedness of the Hilbert transform. The analogue statement also holds for Riesz transforms, which can be found in [Reference Rubio de Francia, Ruiz and Torrea12]. It is well known that Riesz transforms are prototypes of singular integral operators and Fourier multipliers, their boundedness motivates McConnell’s [Reference McConnell9] and Zimmermann’s [Reference Zimmermann19] results on vector-valued Marcinkiewicz–Mihlin multipliers, and motivates Hytönen and Weis’s [Reference Hytönen and Weis6] results on vector-valued singular convolution integrals.
On the other hand,
![]() $T_{\unicode[STIX]{x1D6E4}}$
is well understood when
$T_{\unicode[STIX]{x1D6E4}}$
is well understood when
![]() $\mathbf{X}=\mathbb{R}$
.
$\mathbf{X}=\mathbb{R}$
.
![]() $T_{\unicode[STIX]{x1D6E4}}$
belongs to the class of singular Radon transforms which is connected with the
$T_{\unicode[STIX]{x1D6E4}}$
belongs to the class of singular Radon transforms which is connected with the
![]() $\overline{\unicode[STIX]{x2202}}$
-Neumann problem for pseudo-convex domains [Reference Phong and Stein10] and the boundary behavior of Poisson integral on symmetric spaces [Reference Stein16]. An exposition of the background and related references are to be found in [Reference Stein and Wainger14]. In particular, Stein [Reference Stein17] proved
$\overline{\unicode[STIX]{x2202}}$
-Neumann problem for pseudo-convex domains [Reference Phong and Stein10] and the boundary behavior of Poisson integral on symmetric spaces [Reference Stein16]. An exposition of the background and related references are to be found in [Reference Stein and Wainger14]. In particular, Stein [Reference Stein17] proved
![]() $T_{\unicode[STIX]{x1D6E4}}$
is also bounded on
$T_{\unicode[STIX]{x1D6E4}}$
is also bounded on
![]() $L^{p}(\mathbb{R}^{n})$
, where
$L^{p}(\mathbb{R}^{n})$
, where
![]() $\unicode[STIX]{x1D6E4}(t)=(P_{1}(t),P_{2}(t),\ldots ,P_{n}(t))$
with
$\unicode[STIX]{x1D6E4}(t)=(P_{1}(t),P_{2}(t),\ldots ,P_{n}(t))$
with
![]() $P_{j}$
being polynomials in
$P_{j}$
being polynomials in
![]() $t\in \mathbb{R}^{k}$
.
$t\in \mathbb{R}^{k}$
.
The purpose of my project is to extend the singular integrals theory to a more general setting. More precisely, I am interested in the boundedness of
![]() $T_{\unicode[STIX]{x1D6E4}}$
on Lebesgue–Bôhner spaces
$T_{\unicode[STIX]{x1D6E4}}$
on Lebesgue–Bôhner spaces
![]() $L^{p}(\mathbb{R}^{n};\mathbf{X})$
for some UMD spaces
$L^{p}(\mathbb{R}^{n};\mathbf{X})$
for some UMD spaces
![]() $\mathbf{X}$
and smooth surfaces
$\mathbf{X}$
and smooth surfaces
![]() $\unicode[STIX]{x1D6E4}$
. In fact, I was motivated by the work of Rubio de Francia et al. [Reference Rubio de Francia, Ruiz and Torrea12]; they obtained the boundedness of the Hilbert transform along well-curved curve on
$\unicode[STIX]{x1D6E4}$
. In fact, I was motivated by the work of Rubio de Francia et al. [Reference Rubio de Francia, Ruiz and Torrea12]; they obtained the boundedness of the Hilbert transform along well-curved curve on
![]() $L^{p}(\mathbb{R}^{n};l^{q})$
for
$L^{p}(\mathbb{R}^{n};l^{q})$
for
![]() $1<p,q<\infty$
. So, I start my project by studying the higher- dimensional version and proved the following result:
$1<p,q<\infty$
. So, I start my project by studying the higher- dimensional version and proved the following result:
Theorem A. (See [Reference Liu7])
Let
![]() ${\mathcal{P}}(t)=(P_{1}(t),P_{2}(t),\ldots ,P_{n}(t))$
with
${\mathcal{P}}(t)=(P_{1}(t),P_{2}(t),\ldots ,P_{n}(t))$
with
![]() $P_{j}$
being polynomials in
$P_{j}$
being polynomials in
![]() $t\in \mathbb{R}^{k}$
.
$t\in \mathbb{R}^{k}$
.
![]() $T_{{\mathcal{P}}}$
is bounded on
$T_{{\mathcal{P}}}$
is bounded on
![]() $L^{p}(\mathbb{R}^{n};l^{q})$
,
$L^{p}(\mathbb{R}^{n};l^{q})$
,
![]() $1<p,q<\infty$
; the bounds for the operator do not depend on the coefficients of the polynomial
$1<p,q<\infty$
; the bounds for the operator do not depend on the coefficients of the polynomial
![]() ${\mathcal{P}}$
, but only on the total degree of
${\mathcal{P}}$
, but only on the total degree of
![]() ${\mathcal{P}}$
.
${\mathcal{P}}$
.
Note that
![]() $l^{q}$
is a prototype of UMD spaces. Then, I continued the project and considered the boundedness of the Hilbert transform along homogeneous curves and convex curves on
$l^{q}$
is a prototype of UMD spaces. Then, I continued the project and considered the boundedness of the Hilbert transform along homogeneous curves and convex curves on
![]() $L^{p}(\mathbb{R}^{n};\mathbf{X})$
for some UMD spaces
$L^{p}(\mathbb{R}^{n};\mathbf{X})$
for some UMD spaces
![]() $\mathbf{X}$
; see [Reference Hong and Liu8]. Naturally, it is an interesting problem to extend Theorem A to some more general UMD spaces. Therefore, I study the boundedness of singular integrals
$\mathbf{X}$
; see [Reference Hong and Liu8]. Naturally, it is an interesting problem to extend Theorem A to some more general UMD spaces. Therefore, I study the boundedness of singular integrals
![]() $T_{{\mathcal{P}}}$
on
$T_{{\mathcal{P}}}$
on
![]() $L^{p}(\mathbb{R}^{n};\mathbf{X})$
for
$L^{p}(\mathbb{R}^{n};\mathbf{X})$
for
![]() $1<p<\infty$
and some UMD spaces
$1<p<\infty$
and some UMD spaces
![]() $\mathbf{X}$
in this paper.
$\mathbf{X}$
in this paper.
To present our main result, we need to give some notations. The first definition was introduced by Burkholder [Reference Burkholder4].
Definition 1.1. A Banach space
![]() $\mathbf{X}$
is an UMD space if for some (equivalently, all)
$\mathbf{X}$
is an UMD space if for some (equivalently, all)
![]() $p\in (1,\infty )$
there is a positive constant
$p\in (1,\infty )$
there is a positive constant
![]() $C$
such that
$C$
such that
 $$\begin{eqnarray}\mathop{\left\Vert \mathop{\sum }_{k=1}^{N}\unicode[STIX]{x1D716}_{k}d_{k}\right\Vert }\nolimits_{L^{p}(\unicode[STIX]{x1D707},\mathbf{X})}\leqslant C\mathop{\left\Vert \mathop{\sum }_{k=1}^{N}d_{k}\right\Vert }\nolimits_{L^{p}(\unicode[STIX]{x1D707},\mathbf{X})},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\left\Vert \mathop{\sum }_{k=1}^{N}\unicode[STIX]{x1D716}_{k}d_{k}\right\Vert }\nolimits_{L^{p}(\unicode[STIX]{x1D707},\mathbf{X})}\leqslant C\mathop{\left\Vert \mathop{\sum }_{k=1}^{N}d_{k}\right\Vert }\nolimits_{L^{p}(\unicode[STIX]{x1D707},\mathbf{X})},\end{eqnarray}$$
whenever
![]() $(d_{k})_{k=1}^{N}\in L^{p}(\unicode[STIX]{x1D707},\mathbf{X})^{N}$
is a martingale difference sequence and
$(d_{k})_{k=1}^{N}\in L^{p}(\unicode[STIX]{x1D707},\mathbf{X})^{N}$
is a martingale difference sequence and
![]() $(\unicode[STIX]{x1D716}_{k})_{k=1}^{N}\in \{-1,1\}^{N}$
.
$(\unicode[STIX]{x1D716}_{k})_{k=1}^{N}\in \{-1,1\}^{N}$
.
The second notation is due to Berkson and Gillespie [Reference Berkson and Gillespie2].
Definition 1.2. The class
![]() ${\mathcal{I}}$
consists of those UMD spaces
${\mathcal{I}}$
consists of those UMD spaces
![]() $\mathbf{X}$
which are isomorphic to a closed subspace of a complex interpolation space
$\mathbf{X}$
which are isomorphic to a closed subspace of a complex interpolation space
![]() $[\mathbf{H},\mathbf{Y}]_{\unicode[STIX]{x1D703}}$
,
$[\mathbf{H},\mathbf{Y}]_{\unicode[STIX]{x1D703}}$
,
![]() $0<\unicode[STIX]{x1D703}<1$
, between a Hilbert space
$0<\unicode[STIX]{x1D703}<1$
, between a Hilbert space
![]() $\mathbf{H}$
and another UMD space
$\mathbf{H}$
and another UMD space
![]() $\mathbf{Y}$
.
$\mathbf{Y}$
.
Remark 1.3.
(1)
 ${\mathcal{I}}$
contains almost all standard examples of UMD spaces. In 1986, Rubio de Francia [Reference Rubio de Francia13] proved that for any UMD lattice
${\mathcal{I}}$
contains almost all standard examples of UMD spaces. In 1986, Rubio de Francia [Reference Rubio de Francia13] proved that for any UMD lattice
 $\mathbf{X}$
of functions on a
$\mathbf{X}$
of functions on a
 $\unicode[STIX]{x1D70E}$
-finite measure space there exists
$\unicode[STIX]{x1D70E}$
-finite measure space there exists
 $\unicode[STIX]{x1D703}\in (0,1)$
, Hilbert space
$\unicode[STIX]{x1D703}\in (0,1)$
, Hilbert space
 $\mathbf{H}$
and another UMD lattice
$\mathbf{H}$
and another UMD lattice
 $\mathbf{Y}$
such that
$\mathbf{Y}$
such that
 $\mathbf{X}=[\mathbf{H},\mathbf{Y}]_{\unicode[STIX]{x1D703}}$
. So, every UMD lattice belongs to
$\mathbf{X}=[\mathbf{H},\mathbf{Y}]_{\unicode[STIX]{x1D703}}$
. So, every UMD lattice belongs to
 ${\mathcal{I}}$
. But
${\mathcal{I}}$
. But
 ${\mathcal{I}}$
also contains the Schatten–von Neumann ideals
${\mathcal{I}}$
also contains the Schatten–von Neumann ideals
 $\mathscr{C}^{p}=[\mathscr{C}^{2},\mathscr{C}^{q}]_{\unicode[STIX]{x1D703}}$
,
$\mathscr{C}^{p}=[\mathscr{C}^{2},\mathscr{C}^{q}]_{\unicode[STIX]{x1D703}}$
,
 $1/p=(1-\unicode[STIX]{x1D703})/2+\unicode[STIX]{x1D703}/q$
.
$1/p=(1-\unicode[STIX]{x1D703})/2+\unicode[STIX]{x1D703}/q$
.
 $\mathscr{C}^{p}$
,
$\mathscr{C}^{p}$
,
 $p\neq 2$
, do not have local unconditional structure, then, they are not Banach lattices.
$p\neq 2$
, do not have local unconditional structure, then, they are not Banach lattices.(2) In [Reference Rubio de Francia13], Rubio de Francia posed an open problem, “Is every
 $B\in UMD$
intermediate between a ‘worse’
$B\in UMD$
intermediate between a ‘worse’
 $B_{0}$
and a Hilbert space?”. Its significance is results in UMD spaces can be proved by interpolating with the estimates available in arbitrary UMD spaces and the stronger ones that one can get in a Hilbert space. Thus it is interesting to know if
$B_{0}$
and a Hilbert space?”. Its significance is results in UMD spaces can be proved by interpolating with the estimates available in arbitrary UMD spaces and the stronger ones that one can get in a Hilbert space. Thus it is interesting to know if
 ${\mathcal{I}}$
actually contains all UMD spaces.
${\mathcal{I}}$
actually contains all UMD spaces.
The main result of this paper is the following theorem:
Theorem 1.4. Let
![]() $\mathbf{X}\in {\mathcal{I}}$
,
$\mathbf{X}\in {\mathcal{I}}$
,
![]() ${\mathcal{P}}(t)=(P_{1}(t),P_{2}(t),\ldots ,P_{n}(t))$
with
${\mathcal{P}}(t)=(P_{1}(t),P_{2}(t),\ldots ,P_{n}(t))$
with
![]() $P_{j}$
being polynomials in
$P_{j}$
being polynomials in
![]() $t\in \mathbb{R}^{k}$
. Then for
$t\in \mathbb{R}^{k}$
. Then for
![]() $1<p<\infty$
there exists a constant
$1<p<\infty$
there exists a constant
![]() $C_{p}>0$
such that
$C_{p}>0$
such that
The constant
![]() $C_{p}$
may depend on
$C_{p}$
may depend on
![]() $\mathbf{X}$
,
$\mathbf{X}$
,
![]() $k$
,
$k$
,
![]() $n$
and the total degree of
$n$
and the total degree of
![]() ${\mathcal{P}}$
, but it is independent of the coefficients of
${\mathcal{P}}$
, but it is independent of the coefficients of
![]() ${\mathcal{P}}$
.
${\mathcal{P}}$
.
Remark 1.5. Obviously, Theorem 1.4 is an extension of Stein’s result [Reference Stein17] and Theorem A; the extension is not trivial. In fact, in [Reference Stein17] and [Reference Liu7], it is significant to get the
![]() $L^{p}$
boundedness for the analytic family of operators
$L^{p}$
boundedness for the analytic family of operators
![]() $T_{z}$
, where
$T_{z}$
, where
![]() $\text{Re}(z)$
is negative. The boundedness on
$\text{Re}(z)$
is negative. The boundedness on
![]() $L^{2}$
obtained with the help of the Fourier transform and Plancherel theorem, together with Hörmander condition implies the boundedness on
$L^{2}$
obtained with the help of the Fourier transform and Plancherel theorem, together with Hörmander condition implies the boundedness on
![]() $L^{p}$
for all
$L^{p}$
for all
![]() $1<p<\infty$
. For general Banach-valued functions, we cannot use Fourier transform and Plancherel theorem to get the boundedness on
$1<p<\infty$
. For general Banach-valued functions, we cannot use Fourier transform and Plancherel theorem to get the boundedness on
![]() $L^{2}(\mathbb{R}^{n};\mathbf{X})$
as a priori estimate. It turned out to be a significantly more difficult task to get the boundedness without a priori estimate even for the single
$L^{2}(\mathbb{R}^{n};\mathbf{X})$
as a priori estimate. It turned out to be a significantly more difficult task to get the boundedness without a priori estimate even for the single
![]() $p$
. So, we have to appeal to new techniques.
$p$
. So, we have to appeal to new techniques.
The paper is organized as follows. In Section 2, by using method of descent for vector-valued functions, we imply Theorem 1.4 under the assumption that singular integrals associated to monomials are bounded on
![]() $L^{p}(\mathbb{R}^{n};\mathbf{X})$
. Finally, in Section 3, we show the boundedness of singular integrals associated to monomials on
$L^{p}(\mathbb{R}^{n};\mathbf{X})$
. Finally, in Section 3, we show the boundedness of singular integrals associated to monomials on
![]() $L^{p}(\mathbb{R}^{n};\mathbf{X})$
.
$L^{p}(\mathbb{R}^{n};\mathbf{X})$
.
2 Proof of Theorem 1.4
Let
![]() ${\mathcal{P}}(t)=(P_{1}(t),P_{2}(t),\ldots ,P_{n}(t))$
,
${\mathcal{P}}(t)=(P_{1}(t),P_{2}(t),\ldots ,P_{n}(t))$
,
![]() $d$
denotes the maximum degree of the polynomials
$d$
denotes the maximum degree of the polynomials
![]() $P_{j}(t)$
. We consider the collection of all monomials
$P_{j}(t)$
. We consider the collection of all monomials
![]() $t^{\unicode[STIX]{x1D6FC}}$
with
$t^{\unicode[STIX]{x1D6FC}}$
with
![]() $1\leqslant |\unicode[STIX]{x1D6FC}|\leqslant d$
, let
$1\leqslant |\unicode[STIX]{x1D6FC}|\leqslant d$
, let
![]() $N$
denote the number of these monomials. We work in
$N$
denote the number of these monomials. We work in
![]() $\mathbb{R}^{N}$
, whose coordinates are labeled by the multi-indices
$\mathbb{R}^{N}$
, whose coordinates are labeled by the multi-indices
![]() $\unicode[STIX]{x1D6FC}$
with
$\unicode[STIX]{x1D6FC}$
with
![]() $1\leqslant |\unicode[STIX]{x1D6FC}|\leqslant d$
, that is,
$1\leqslant |\unicode[STIX]{x1D6FC}|\leqslant d$
, that is,
![]() $\mathbb{R}^{N}=\{(x_{\unicode[STIX]{x1D6FC}})_{1\leqslant |\unicode[STIX]{x1D6FC}|\leqslant d}\}$
. Let
$\mathbb{R}^{N}=\{(x_{\unicode[STIX]{x1D6FC}})_{1\leqslant |\unicode[STIX]{x1D6FC}|\leqslant d}\}$
. Let
![]() $\mathfrak{p}$
be a polynomial map from
$\mathfrak{p}$
be a polynomial map from
![]() $\mathbb{R}^{k}$
to
$\mathbb{R}^{k}$
to
![]() $\mathbb{R}^{N}$
, precisely,
$\mathbb{R}^{N}$
, precisely,
![]() $\mathfrak{p}(t)=(t^{\unicode[STIX]{x1D6FC}})_{1\leqslant |\unicode[STIX]{x1D6FC}|\leqslant d}$
. For
$\mathfrak{p}(t)=(t^{\unicode[STIX]{x1D6FC}})_{1\leqslant |\unicode[STIX]{x1D6FC}|\leqslant d}$
. For
![]() $f\in \mathscr{S}(\mathbb{R}^{N};\mathbf{X})$
, we define singular integrals by
$f\in \mathscr{S}(\mathbb{R}^{N};\mathbf{X})$
, we define singular integrals by
Clearly, it can be looked as a model case of
![]() $T_{{\mathcal{P}}}$
. To prove Theorem 1.4, we accept the following inequality for a moment,
$T_{{\mathcal{P}}}$
. To prove Theorem 1.4, we accept the following inequality for a moment,
which will be proved in the next section.
We also need the method of descent for vector-valued functions that allows us to pass from results about operators in one
![]() $\mathbb{R}^{N}$
to corresponding operators on another
$\mathbb{R}^{N}$
to corresponding operators on another
![]() $\mathbb{R}^{n}$
. The following lemma is a vector-valued version of Ricci and Stein’s “method of transference” (see [Reference Ricci and Stein11, Proposition 5.1] and [Reference Stein18, p. 483]); it can be proved in a similar way.
$\mathbb{R}^{n}$
. The following lemma is a vector-valued version of Ricci and Stein’s “method of transference” (see [Reference Ricci and Stein11, Proposition 5.1] and [Reference Stein18, p. 483]); it can be proved in a similar way.
Let
![]() $T$
be given by convolution with a distribution
$T$
be given by convolution with a distribution
![]() $d\unicode[STIX]{x1D707}$
,
$d\unicode[STIX]{x1D707}$
,
![]() $Tf=f\ast d\unicode[STIX]{x1D707}$
, where
$Tf=f\ast d\unicode[STIX]{x1D707}$
, where
![]() $f$
is an appropriate vector-valued function on
$f$
is an appropriate vector-valued function on
![]() $\mathbb{R}^{N}$
. We fix a linear mapping
$\mathbb{R}^{N}$
. We fix a linear mapping
![]() $L$
from
$L$
from
![]() $\mathbb{R}^{N}$
to
$\mathbb{R}^{N}$
to
![]() $\mathbb{R}^{n}$
; the operator
$\mathbb{R}^{n}$
; the operator
![]() $T^{L}$
is defined by
$T^{L}$
is defined by
where
![]() $f$
is an appropriate vector-valued function on
$f$
is an appropriate vector-valued function on
![]() $\mathbb{R}^{n}$
. In fact,
$\mathbb{R}^{n}$
. In fact,
![]() $T^{L}$
is a convolution operator on
$T^{L}$
is a convolution operator on
![]() $\mathbb{R}^{n}$
with the
$\mathbb{R}^{n}$
with the
![]() $d\unicode[STIX]{x1D707}^{L}$
, where
$d\unicode[STIX]{x1D707}^{L}$
, where
![]() $d\unicode[STIX]{x1D707}^{L}$
is defined by
$d\unicode[STIX]{x1D707}^{L}$
is defined by
Lemma 2.1. Suppose
![]() $L:\mathbb{R}^{N}\rightarrow \mathbb{R}^{n}$
is a fixed linear mapping as above. Then the norm of the operator
$L:\mathbb{R}^{N}\rightarrow \mathbb{R}^{n}$
is a fixed linear mapping as above. Then the norm of the operator
![]() $T^{L}$
acting on
$T^{L}$
acting on
![]() $L^{p}(\mathbb{R}^{n};\mathbf{X})$
does not exceed the norm of
$L^{p}(\mathbb{R}^{n};\mathbf{X})$
does not exceed the norm of
![]() $T$
acting on
$T$
acting on
![]() $L^{p}(\mathbb{R}^{N};\mathbf{X})$
for
$L^{p}(\mathbb{R}^{N};\mathbf{X})$
for
![]() $1<p<\infty$
.
$1<p<\infty$
.
To prove Theorem 1.4, we define a distribution
![]() $d\unicode[STIX]{x1D707}$
on
$d\unicode[STIX]{x1D707}$
on
![]() $\mathbb{R}^{N}$
by
$\mathbb{R}^{N}$
by
Then,
![]() $T_{\mathfrak{p}}f=f\ast d\unicode[STIX]{x1D707}$
. We set
$T_{\mathfrak{p}}f=f\ast d\unicode[STIX]{x1D707}$
. We set
Using the coefficients
![]() $a_{j\unicode[STIX]{x1D6FC}}$
, we define a linear mapping
$a_{j\unicode[STIX]{x1D6FC}}$
, we define a linear mapping
![]() $L:\mathbb{R}^{N}\rightarrow \mathbb{R}^{n}$
, where the coordinates of
$L:\mathbb{R}^{N}\rightarrow \mathbb{R}^{n}$
, where the coordinates of
![]() $L(x)$
are given by
$L(x)$
are given by
with
![]() $x=(x_{\unicode[STIX]{x1D6FC}})\in \mathbb{R}^{N}$
.
$x=(x_{\unicode[STIX]{x1D6FC}})\in \mathbb{R}^{N}$
.
![]() $d\unicode[STIX]{x1D707}^{L}$
is given by
$d\unicode[STIX]{x1D707}^{L}$
is given by
By Lemma 2.1, we have
Finally, the boundedness of
![]() $T_{\mathfrak{p}}$
on
$T_{\mathfrak{p}}$
on
![]() $L^{p}(\mathbb{R}^{N};\mathbf{X})$
implies our main result.
$L^{p}(\mathbb{R}^{N};\mathbf{X})$
implies our main result.
3 Proof of (2.1)
First, we define a one-parameter family of dilations relevant
![]() $\mathfrak{p}$
, which is given by
$\mathfrak{p}$
, which is given by
for
![]() $x\in \mathbb{R}^{N}$
. We also define related norm
$x\in \mathbb{R}^{N}$
. We also define related norm
where
![]() $a_{i}=\prod _{j\neq i}|\unicode[STIX]{x1D6FC}^{j}|$
, the quasi-distance is
$a_{i}=\prod _{j\neq i}|\unicode[STIX]{x1D6FC}^{j}|$
, the quasi-distance is
![]() $\unicode[STIX]{x1D70C}(x,y)=\unicode[STIX]{x1D70C}(x-y)$
. It is trivial that
$\unicode[STIX]{x1D70C}(x,y)=\unicode[STIX]{x1D70C}(x-y)$
. It is trivial that
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FF}\circ x)=\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70C}(x)$
, we also have the following properties:
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FF}\circ x)=\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70C}(x)$
, we also have the following properties:
Lemma 3.1. If
![]() $\unicode[STIX]{x1D70C}(x)\geqslant 1$
, then
$\unicode[STIX]{x1D70C}(x)\geqslant 1$
, then
![]() $\unicode[STIX]{x1D70C}(x)\leqslant |x|$
; If
$\unicode[STIX]{x1D70C}(x)\leqslant |x|$
; If
![]() $\unicode[STIX]{x1D70C}(x)\leqslant 1$
, then
$\unicode[STIX]{x1D70C}(x)\leqslant 1$
, then
![]() $|x|\leqslant \unicode[STIX]{x1D70C}(x)$
.
$|x|\leqslant \unicode[STIX]{x1D70C}(x)$
.
For
![]() $z\in \mathbb{C}$
, we define an analytic family of operators
$z\in \mathbb{C}$
, we define an analytic family of operators
![]() $T_{\mathfrak{p}}^{z}$
by
$T_{\mathfrak{p}}^{z}$
by
where
![]() $m^{z}$
are given by
$m^{z}$
are given by
Obviously,
![]() $T_{\mathfrak{p}}^{0}$
is the original operator
$T_{\mathfrak{p}}^{0}$
is the original operator
![]() $T_{\mathfrak{p}}$
.
$T_{\mathfrak{p}}$
.
3.1 The boundedness of
 $T_{\mathfrak{p}}^{z}$
on
$T_{\mathfrak{p}}^{z}$
on
 $L^{2}\big(\mathbb{R}^{N};\mathbf{H}\big)$
$L^{2}\big(\mathbb{R}^{N};\mathbf{H}\big)$
In this subsection, we prove that
where
![]() $\text{Re}(z)<\frac{1}{d}$
and
$\text{Re}(z)<\frac{1}{d}$
and
![]() $C(z)$
grows at most polynomially in
$C(z)$
grows at most polynomially in
![]() $(1+|\text{Im}(z)|)$
. Clearly, the boundedness of
$(1+|\text{Im}(z)|)$
. Clearly, the boundedness of
![]() $T_{\mathfrak{p}}^{z}$
on
$T_{\mathfrak{p}}^{z}$
on
![]() $L^{2}\big(\mathbb{R}^{N};\mathbf{H}\big)$
is equivalent to the uniform boundedness of
$L^{2}\big(\mathbb{R}^{N};\mathbf{H}\big)$
is equivalent to the uniform boundedness of
![]() $m^{z}(\unicode[STIX]{x1D709})$
. Thus, we just need to show that
$m^{z}(\unicode[STIX]{x1D709})$
. Thus, we just need to show that
Suppose that
![]() $\unicode[STIX]{x1D713}\in C_{0}^{\infty }(\mathbb{R}^{k})$
is radial, vanishes near the origin and satisfies
$\unicode[STIX]{x1D713}\in C_{0}^{\infty }(\mathbb{R}^{k})$
is radial, vanishes near the origin and satisfies
For
![]() $j\in \mathbb{Z}$
, we also define
$j\in \mathbb{Z}$
, we also define
![]() $m_{j}^{z}$
by
$m_{j}^{z}$
by
Then we have equations
With above preparation, we begin the proof of (3.1).
Proof. For fixed
![]() $\unicode[STIX]{x1D709}$
with
$\unicode[STIX]{x1D709}$
with
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})\leqslant 1$
, we have
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})\leqslant 1$
, we have
 $$\begin{eqnarray}\displaystyle |m_{0}^{z}(\unicode[STIX]{x1D709})| & = & \displaystyle \{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})\}^{\text{Re}(z)}\left|\int _{\mathbb{R}^{k}}e^{-2\unicode[STIX]{x1D70B}i\mathfrak{p}(t)\cdot \unicode[STIX]{x1D709}}|t|^{z}K(t)\unicode[STIX]{x1D713}(t)\,dt\right|\nonumber\\ \displaystyle & = & \displaystyle \{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})\}^{\text{Re}(z)}\left|\int _{\mathbb{R}^{k}}[e^{-2\unicode[STIX]{x1D70B}i\mathfrak{p}(t)\cdot \unicode[STIX]{x1D709}}-1]|t|^{z}K(t)\unicode[STIX]{x1D713}(t)\,dt\right|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C(z)|\unicode[STIX]{x1D709}|\leqslant C(z)\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |m_{0}^{z}(\unicode[STIX]{x1D709})| & = & \displaystyle \{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})\}^{\text{Re}(z)}\left|\int _{\mathbb{R}^{k}}e^{-2\unicode[STIX]{x1D70B}i\mathfrak{p}(t)\cdot \unicode[STIX]{x1D709}}|t|^{z}K(t)\unicode[STIX]{x1D713}(t)\,dt\right|\nonumber\\ \displaystyle & = & \displaystyle \{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})\}^{\text{Re}(z)}\left|\int _{\mathbb{R}^{k}}[e^{-2\unicode[STIX]{x1D70B}i\mathfrak{p}(t)\cdot \unicode[STIX]{x1D709}}-1]|t|^{z}K(t)\unicode[STIX]{x1D713}(t)\,dt\right|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C(z)|\unicode[STIX]{x1D709}|\leqslant C(z)\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709}).\nonumber\end{eqnarray}$$
Note that
![]() $\mathfrak{p}(t)$
is of finite type at each point, and is indeed of type at most
$\mathfrak{p}(t)$
is of finite type at each point, and is indeed of type at most
![]() $d$
. For
$d$
. For
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})>1$
, by [Reference Stein18, Theorem 2 of Chapter 8] and Lemma 3.1, we have
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})>1$
, by [Reference Stein18, Theorem 2 of Chapter 8] and Lemma 3.1, we have
 $$\begin{eqnarray}\displaystyle |m_{0}^{z}(\unicode[STIX]{x1D709})| & = & \displaystyle \{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})\}^{\text{Re}(z)}\left|\int _{\mathbb{R}^{k}}e^{-2\unicode[STIX]{x1D70B}i\mathfrak{p}(t)\cdot \unicode[STIX]{x1D709}}|t|^{z}K(t)\unicode[STIX]{x1D713}(t)\,dt\right|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C(z)\{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})\}^{\text{Re}(z)}|\unicode[STIX]{x1D709}|^{-1/d}\leqslant C(z)\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})^{\text{Re}(z)-1/d}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |m_{0}^{z}(\unicode[STIX]{x1D709})| & = & \displaystyle \{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})\}^{\text{Re}(z)}\left|\int _{\mathbb{R}^{k}}e^{-2\unicode[STIX]{x1D70B}i\mathfrak{p}(t)\cdot \unicode[STIX]{x1D709}}|t|^{z}K(t)\unicode[STIX]{x1D713}(t)\,dt\right|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C(z)\{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})\}^{\text{Re}(z)}|\unicode[STIX]{x1D709}|^{-1/d}\leqslant C(z)\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})^{\text{Re}(z)-1/d}.\nonumber\end{eqnarray}$$
Finally, we use above two estimates and the fact
![]() $\text{Re}(z)<\frac{1}{d}$
, then
$\text{Re}(z)<\frac{1}{d}$
, then
 $$\begin{eqnarray}\displaystyle |m^{z}(\unicode[STIX]{x1D709})|=\left|\mathop{\sum }_{j\in \mathbb{Z}}m_{0}^{z}(2^{-j}\circ \unicode[STIX]{x1D709})\right| & {\leqslant} & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70C}(2^{-j}\circ \unicode[STIX]{x1D709})\leqslant 1}|m_{0}^{z}(2^{-j}\circ \unicode[STIX]{x1D709})|\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{\unicode[STIX]{x1D70C}(2^{-j}\circ \unicode[STIX]{x1D709})>1}|m_{0}^{z}(2^{-j}\circ \unicode[STIX]{x1D709})|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C(z)\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})\mathop{\sum }_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})\leqslant 2^{j}}2^{-j}+C(z)\{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})\}^{\text{Re}(z)-1/d}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})>2^{j}}2^{-j[\text{Re}(z)-1/d]}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C(z).\square\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |m^{z}(\unicode[STIX]{x1D709})|=\left|\mathop{\sum }_{j\in \mathbb{Z}}m_{0}^{z}(2^{-j}\circ \unicode[STIX]{x1D709})\right| & {\leqslant} & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70C}(2^{-j}\circ \unicode[STIX]{x1D709})\leqslant 1}|m_{0}^{z}(2^{-j}\circ \unicode[STIX]{x1D709})|\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{\unicode[STIX]{x1D70C}(2^{-j}\circ \unicode[STIX]{x1D709})>1}|m_{0}^{z}(2^{-j}\circ \unicode[STIX]{x1D709})|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C(z)\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})\mathop{\sum }_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})\leqslant 2^{j}}2^{-j}+C(z)\{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})\}^{\text{Re}(z)-1/d}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})>2^{j}}2^{-j[\text{Re}(z)-1/d]}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C(z).\square\nonumber\end{eqnarray}$$
3.2 The boundedness of
 $T_{\mathfrak{p}}^{z}$
on
$T_{\mathfrak{p}}^{z}$
on
 $L^{p}(\mathbb{R}^{n};\mathbf{Y})$
$L^{p}(\mathbb{R}^{n};\mathbf{Y})$
The next goal is to prove that
where
![]() $\unicode[STIX]{x1D6FD}$
is some positive constant and
$\unicode[STIX]{x1D6FD}$
is some positive constant and
![]() $C(z)$
grows at most polynomially in
$C(z)$
grows at most polynomially in
![]() $(1+|\text{Im}(z)|)$
.
$(1+|\text{Im}(z)|)$
.
In [Reference Stein18, p. 514], the
![]() $L^{2}$
boundedness of analytic singular integrals, together with Hörmander condition, implies the boundedness on
$L^{2}$
boundedness of analytic singular integrals, together with Hörmander condition, implies the boundedness on
![]() $L^{p}$
for all
$L^{p}$
for all
![]() $p\in (1,\infty )$
. This argument is also true for a general situation of vector-valued functions. In Hilbert space, the
$p\in (1,\infty )$
. This argument is also true for a general situation of vector-valued functions. In Hilbert space, the
![]() $L^{2}$
boundedness is obtained for free with the help of the Fourier transform and Plancherel’s theorem. However, for general UMD space
$L^{2}$
boundedness is obtained for free with the help of the Fourier transform and Plancherel’s theorem. However, for general UMD space
![]() $\mathbf{Y}$
, Plancherel’s theorem does not hold anymore; it is a difficult task to get the boundedness of analytic singular integrals on
$\mathbf{Y}$
, Plancherel’s theorem does not hold anymore; it is a difficult task to get the boundedness of analytic singular integrals on
![]() $L^{2}(\mathbb{R}^{N};\mathbf{Y})$
, even for any single
$L^{2}(\mathbb{R}^{N};\mathbf{Y})$
, even for any single
![]() $p_{0}$
. The following theorem gives the conditions on the singular kernel to yield a singular integral operator bounded on
$p_{0}$
. The following theorem gives the conditions on the singular kernel to yield a singular integral operator bounded on
![]() $L^{p}(\mathbb{R}^{N};\mathbf{Y})$
, which is a partial generalization of [Reference Hytönen5, Corollary 4.2] and can be prove in a similar way.
$L^{p}(\mathbb{R}^{N};\mathbf{Y})$
, which is a partial generalization of [Reference Hytönen5, Corollary 4.2] and can be prove in a similar way.
Theorem 3.2. Let
![]() $\mathbf{Y}$
be an UMD space, and
$\mathbf{Y}$
be an UMD space, and
![]() $\mathbf{K}\in \mathscr{S}^{\prime }(\mathbb{R}^{N})$
. The anisotropic dilations are given by
$\mathbf{K}\in \mathscr{S}^{\prime }(\mathbb{R}^{N})$
. The anisotropic dilations are given by
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D706}}x=(\unicode[STIX]{x1D706}^{b_{1}}x_{1},\unicode[STIX]{x1D706}^{b_{2}}x_{2},\ldots ,\unicode[STIX]{x1D706}^{b_{N}}x_{N})$
with
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D706}}x=(\unicode[STIX]{x1D706}^{b_{1}}x_{1},\unicode[STIX]{x1D706}^{b_{2}}x_{2},\ldots ,\unicode[STIX]{x1D706}^{b_{N}}x_{N})$
with
![]() $b_{i}>0$
, the respected norm function is denoted by
$b_{i}>0$
, the respected norm function is denoted by
![]() $\unicode[STIX]{x1D70C}(x)$
. Suppose
$\unicode[STIX]{x1D70C}(x)$
. Suppose
![]() $\mathbf{K}$
has the homogeneity property
$\mathbf{K}$
has the homogeneity property
![]() $\unicode[STIX]{x1D706}^{b}\mathbf{K}(\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D706}}x)=\mathbf{K}(x)$
with
$\unicode[STIX]{x1D706}^{b}\mathbf{K}(\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D706}}x)=\mathbf{K}(x)$
with
![]() $b=\sum b_{i}$
,
$b=\sum b_{i}$
,
![]() $\mathbf{K}$
also satisfies the following conditions
$\mathbf{K}$
also satisfies the following conditions
and
for some
![]() $C_{0}\geqslant 6$
. Then
$C_{0}\geqslant 6$
. Then
![]() $f\in \mathscr{S}(\mathbb{R}^{N};\mathbf{Y})\mapsto \mathbf{K}\ast f$
extends to a bounded linear operator
$f\in \mathscr{S}(\mathbb{R}^{N};\mathbf{Y})\mapsto \mathbf{K}\ast f$
extends to a bounded linear operator
with norm at most
![]() $C(A_{0}+A_{1})$
, where
$C(A_{0}+A_{1})$
, where
![]() $C$
is a geometric constant.
$C$
is a geometric constant.
We now use Theorem 3.2 to prove (3.2). We set
![]() $\unicode[STIX]{x1D6E5}=\sum _{1\leqslant |\unicode[STIX]{x1D6FC}|\leqslant d}|\unicode[STIX]{x1D6FC}|$
. For
$\unicode[STIX]{x1D6E5}=\sum _{1\leqslant |\unicode[STIX]{x1D6FC}|\leqslant d}|\unicode[STIX]{x1D6FC}|$
. For
![]() $-\unicode[STIX]{x1D6E5}<\text{Re}(z)<0$
,
$-\unicode[STIX]{x1D6E5}<\text{Re}(z)<0$
,
![]() $h_{z}(x)$
and
$h_{z}(x)$
and
![]() $K_{z}(x)$
are given by
$K_{z}(x)$
are given by
respectively. Obviously,
For
![]() $f\in \mathscr{S}(\mathbb{R}^{N};\mathbf{Y})$
, we see that
$f\in \mathscr{S}(\mathbb{R}^{N};\mathbf{Y})$
, we see that
It suffices to verify
![]() $K_{z}$
satisfying conditions in Theorem 3.2. So, we need the following lemma which can be found in [Reference Stein and Wainger14, p. 1272].
$K_{z}$
satisfying conditions in Theorem 3.2. So, we need the following lemma which can be found in [Reference Stein and Wainger14, p. 1272].
Lemma 3.3. Let
![]() $h_{z}$
and
$h_{z}$
and
![]() $K_{z}$
be given as above. Then
$K_{z}$
be given as above. Then
![]() $h_{z}(x)$
is a locally integrable function,
$h_{z}(x)$
is a locally integrable function,
![]() $C^{\infty }$
away from the origin satisfying
$C^{\infty }$
away from the origin satisfying
Moreover, each derivative of
![]() $h_{z}(x)$
is bounded by a polynomial in
$h_{z}(x)$
is bounded by a polynomial in
![]() $|z|$
, if
$|z|$
, if
![]() $\unicode[STIX]{x1D70C}(x)=1$
. In particular,
$\unicode[STIX]{x1D70C}(x)=1$
. In particular,
![]() $K_{z}$
has the homogeneity property
$K_{z}$
has the homogeneity property
![]() $\unicode[STIX]{x1D706}^{\unicode[STIX]{x1D6E5}}K_{z}(\unicode[STIX]{x1D706}\circ x)=K_{z}(x)$
.
$\unicode[STIX]{x1D706}^{\unicode[STIX]{x1D6E5}}K_{z}(\unicode[STIX]{x1D706}\circ x)=K_{z}(x)$
.
According to the Fourier estimate in Section 3.1, we obtain that
To verify
![]() $K_{z}$
satisfying (3.3), we may assume that
$K_{z}$
satisfying (3.3), we may assume that
![]() $\unicode[STIX]{x1D70C}(y)=1$
and just need to prove that
$\unicode[STIX]{x1D70C}(y)=1$
and just need to prove that
In fact, we set
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D70C}(y)$
and
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D70C}(y)$
and
![]() $y^{\prime }=y/\unicode[STIX]{x1D706}$
. Obviously,
$y^{\prime }=y/\unicode[STIX]{x1D706}$
. Obviously,
![]() $\unicode[STIX]{x1D70C}(y^{\prime })=1$
. By a linear transformation
$\unicode[STIX]{x1D70C}(y^{\prime })=1$
. By a linear transformation
![]() $x=\unicode[STIX]{x1D706}\circ x^{\prime }$
, notice the homogeneity of
$x=\unicode[STIX]{x1D706}\circ x^{\prime }$
, notice the homogeneity of
![]() $K_{z}$
, we have
$K_{z}$
, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}\unicode[STIX]{x1D70C}(y)}|K_{z}(x-y)-K_{z}(x)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\unicode[STIX]{x1D70C}(x^{\prime })\geqslant C_{0}}|K_{z}(x^{\prime }-y^{\prime })-K_{z}(x^{\prime })|\log ^{N}(e+\unicode[STIX]{x1D706}\unicode[STIX]{x1D70C}(x^{\prime }))\,dx^{\prime }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}\unicode[STIX]{x1D70C}(y)}|K_{z}(x-y)-K_{z}(x)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\unicode[STIX]{x1D70C}(x^{\prime })\geqslant C_{0}}|K_{z}(x^{\prime }-y^{\prime })-K_{z}(x^{\prime })|\log ^{N}(e+\unicode[STIX]{x1D706}\unicode[STIX]{x1D70C}(x^{\prime }))\,dx^{\prime }.\nonumber\end{eqnarray}$$
If
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D70C}(y)\geqslant 6$
, it is trivial that
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D70C}(y)\geqslant 6$
, it is trivial that
where we use the fact
![]() $C_{0}\geqslant 6$
. By (3.4), we obtain
$C_{0}\geqslant 6$
. By (3.4), we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}\unicode[STIX]{x1D70C}(y)}|K_{z}(x-y)-K_{z}(x)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{\unicode[STIX]{x1D70C}(x^{\prime })\geqslant C_{0}}|K_{z}(x^{\prime }-y^{\prime })-K_{z}(x^{\prime })|\log ^{N}(e+\unicode[STIX]{x1D70C}(x^{\prime }))\,dx^{\prime }\log ^{N}(e+\unicode[STIX]{x1D70C}(y))\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(z)\log ^{N}(e+\unicode[STIX]{x1D70C}(y)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}\unicode[STIX]{x1D70C}(y)}|K_{z}(x-y)-K_{z}(x)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{\unicode[STIX]{x1D70C}(x^{\prime })\geqslant C_{0}}|K_{z}(x^{\prime }-y^{\prime })-K_{z}(x^{\prime })|\log ^{N}(e+\unicode[STIX]{x1D70C}(x^{\prime }))\,dx^{\prime }\log ^{N}(e+\unicode[STIX]{x1D70C}(y))\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(z)\log ^{N}(e+\unicode[STIX]{x1D70C}(y)).\nonumber\end{eqnarray}$$
When
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D70C}(y)<6$
, using (3.4), we have
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D70C}(y)<6$
, using (3.4), we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}\unicode[STIX]{x1D70C}(y)}|K_{z}(x-y)-K_{z}(x)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2^{n}\int _{\unicode[STIX]{x1D70C}(x^{\prime })\geqslant C_{0}}|K_{z}(x^{\prime }-y^{\prime })-K_{z}(x^{\prime })|\log ^{N}(e+\unicode[STIX]{x1D70C}(x^{\prime }))\,dx^{\prime }\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(z)\leqslant C(z)\log ^{N}(e+\unicode[STIX]{x1D70C}(y)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}\unicode[STIX]{x1D70C}(y)}|K_{z}(x-y)-K_{z}(x)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2^{n}\int _{\unicode[STIX]{x1D70C}(x^{\prime })\geqslant C_{0}}|K_{z}(x^{\prime }-y^{\prime })-K_{z}(x^{\prime })|\log ^{N}(e+\unicode[STIX]{x1D70C}(x^{\prime }))\,dx^{\prime }\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(z)\leqslant C(z)\log ^{N}(e+\unicode[STIX]{x1D70C}(y)).\nonumber\end{eqnarray}$$
To prove (3.4), we define
![]() $K_{z}^{1}$
and
$K_{z}^{1}$
and
![]() $K_{z}^{2}$
by
$K_{z}^{2}$
by
respectively. We split the integral as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}|K_{z}(x-y)-K_{z}(x)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}|K_{z}^{1}(x)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}|K_{z}^{1}(x-y)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}|K_{z}^{2}(x-y)-K_{z}^{2}(x)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}|K_{z}(x-y)-K_{z}(x)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}|K_{z}^{1}(x)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}|K_{z}^{1}(x-y)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}|K_{z}^{2}(x-y)-K_{z}^{2}(x)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx.\nonumber\end{eqnarray}$$
To estimate first two summands, we need a estimate related to
![]() $h_{z}$
, which can be found in [Reference Stein and Wainger14, p. 1273]. The homogeneity of
$h_{z}$
, which can be found in [Reference Stein and Wainger14, p. 1273]. The homogeneity of
![]() $h_{z}$
and the smoothness of
$h_{z}$
and the smoothness of
![]() $h_{z}$
away from
$h_{z}$
away from
![]() $0$
imply that
$0$
imply that
for some
![]() $\unicode[STIX]{x1D707}>0$
, provided
$\unicode[STIX]{x1D707}>0$
, provided
![]() $|y|/|x|$
is sufficiently small.
$|y|/|x|$
is sufficiently small.
We set
![]() $\unicode[STIX]{x1D6FD}=\min \{\unicode[STIX]{x1D707},1\}$
. For the first integral, by using Fubini theorem and (3.5), we have
$\unicode[STIX]{x1D6FD}=\min \{\unicode[STIX]{x1D707},1\}$
. For the first integral, by using Fubini theorem and (3.5), we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}|K_{z}^{1}(x)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}\int _{|t|\leqslant 1}|h_{z}(x-\mathfrak{p}(t))-h_{z}(x)||t|^{\text{Re}(z)-k}\,dt\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{|t|\leqslant 1}|t|^{\text{Re}(z)-k}\int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}|h_{z}(x-\mathfrak{p}(t))-h_{z}(x)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{|t|\leqslant 1}|t|^{\text{Re}(z)-k}|\mathfrak{p}(t)|\int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}\unicode[STIX]{x1D70C}(x)^{-[\unicode[STIX]{x1D6E5}+\text{Re}(z)+\unicode[STIX]{x1D707}]}\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{|t|\leqslant 1}|t|^{\text{Re}(z)-k}|\mathfrak{p}(t)|\int _{{\mathcal{S}}^{N-1}}\int _{C_{0}}^{\infty }r^{-[1+\text{Re}(z)+\unicode[STIX]{x1D707}]}\log ^{N}(e+r)\,dr\,d\unicode[STIX]{x1D714}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(z),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}|K_{z}^{1}(x)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}\int _{|t|\leqslant 1}|h_{z}(x-\mathfrak{p}(t))-h_{z}(x)||t|^{\text{Re}(z)-k}\,dt\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{|t|\leqslant 1}|t|^{\text{Re}(z)-k}\int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}|h_{z}(x-\mathfrak{p}(t))-h_{z}(x)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{|t|\leqslant 1}|t|^{\text{Re}(z)-k}|\mathfrak{p}(t)|\int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}\unicode[STIX]{x1D70C}(x)^{-[\unicode[STIX]{x1D6E5}+\text{Re}(z)+\unicode[STIX]{x1D707}]}\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{|t|\leqslant 1}|t|^{\text{Re}(z)-k}|\mathfrak{p}(t)|\int _{{\mathcal{S}}^{N-1}}\int _{C_{0}}^{\infty }r^{-[1+\text{Re}(z)+\unicode[STIX]{x1D707}]}\log ^{N}(e+r)\,dr\,d\unicode[STIX]{x1D714}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(z),\nonumber\end{eqnarray}$$
where we use the fact that
![]() $-\unicode[STIX]{x1D6FD}<\text{Re}(z)<0$
and coordinatize
$-\unicode[STIX]{x1D6FD}<\text{Re}(z)<0$
and coordinatize
![]() $\mathbb{R}^{N}$
by
$\mathbb{R}^{N}$
by
![]() $r$
and
$r$
and
![]() $\unicode[STIX]{x1D714}$
with
$\unicode[STIX]{x1D714}$
with
![]() $r=\unicode[STIX]{x1D70C}(x)$
and
$r=\unicode[STIX]{x1D70C}(x)$
and
![]() $\unicode[STIX]{x1D714}=\frac{1}{r}\circ x$
.
$\unicode[STIX]{x1D714}=\frac{1}{r}\circ x$
.
The norm function
![]() $\unicode[STIX]{x1D70C}(x)$
has the property of
$\unicode[STIX]{x1D70C}(x)$
has the property of
![]() $\unicode[STIX]{x1D70C}(x+y)\leqslant c(\unicode[STIX]{x1D70C}(x)+\unicode[STIX]{x1D70C}(y))$
for some
$\unicode[STIX]{x1D70C}(x+y)\leqslant c(\unicode[STIX]{x1D70C}(x)+\unicode[STIX]{x1D70C}(y))$
for some
![]() $c>0$
(see [Reference Stein and Wainger14, Propositions 1–9]). Specially, we set
$c>0$
(see [Reference Stein and Wainger14, Propositions 1–9]). Specially, we set
![]() $C_{0}\geqslant \max \{6,3c\}$
. Note that
$C_{0}\geqslant \max \{6,3c\}$
. Note that
![]() $\unicode[STIX]{x1D70C}(x-y)\geqslant \frac{1}{c}\unicode[STIX]{x1D70C}(x)-\unicode[STIX]{x1D70C}(y)\geqslant \frac{C_{0}}{c}-1\geqslant 2$
and
$\unicode[STIX]{x1D70C}(x-y)\geqslant \frac{1}{c}\unicode[STIX]{x1D70C}(x)-\unicode[STIX]{x1D70C}(y)\geqslant \frac{C_{0}}{c}-1\geqslant 2$
and
![]() $\unicode[STIX]{x1D70C}(x)\leqslant c[\unicode[STIX]{x1D70C}(x-y)+\unicode[STIX]{x1D70C}(y)]\leqslant c\unicode[STIX]{x1D70C}(x-y)+c$
. Using a linear transformation, the second summand can be treated as the first one, then
$\unicode[STIX]{x1D70C}(x)\leqslant c[\unicode[STIX]{x1D70C}(x-y)+\unicode[STIX]{x1D70C}(y)]\leqslant c\unicode[STIX]{x1D70C}(x-y)+c$
. Using a linear transformation, the second summand can be treated as the first one, then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}|K_{z}^{1}(x-y)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{\unicode[STIX]{x1D70C}(x)\geqslant 2}|K_{z}^{1}(x)|\log ^{N}(e+c+c\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(z).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}|K_{z}^{1}(x-y)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{\unicode[STIX]{x1D70C}(x)\geqslant 2}|K_{z}^{1}(x)|\log ^{N}(e+c+c\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(z).\nonumber\end{eqnarray}$$
Finally, using Fubini theorem, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}|K_{z}^{2}(x-y)-K_{z}^{2}(x)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{|t|>1}\int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}|h_{z}(x-y-\mathfrak{p}(t))-h_{z}(x-\mathfrak{p}(t))|\nonumber\\ \displaystyle & & \displaystyle \qquad \times \log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx|t|^{\text{Re}(z)-k}\,dt.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}|K_{z}^{2}(x-y)-K_{z}^{2}(x)|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{|t|>1}\int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{0}}|h_{z}(x-y-\mathfrak{p}(t))-h_{z}(x-\mathfrak{p}(t))|\nonumber\\ \displaystyle & & \displaystyle \qquad \times \log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx|t|^{\text{Re}(z)-k}\,dt.\nonumber\end{eqnarray}$$
We divide the inner integral above according to the distance between
![]() $x$
and
$x$
and
![]() $\mathfrak{p}(t)$
. Note that
$\mathfrak{p}(t)$
. Note that
![]() $\unicode[STIX]{x1D70C}(y)=1$
, if
$\unicode[STIX]{x1D70C}(y)=1$
, if
![]() $|y|/|x-\mathfrak{p}(t)|$
is sufficient small, that is
$|y|/|x-\mathfrak{p}(t)|$
is sufficient small, that is
![]() $|x-\mathfrak{p}(t)|$
is away from the origin, we can get that
$|x-\mathfrak{p}(t)|$
is away from the origin, we can get that
![]() $\unicode[STIX]{x1D70C}(x-\mathfrak{p}(t))\geqslant C_{1}$
for an appropriate constant
$\unicode[STIX]{x1D70C}(x-\mathfrak{p}(t))\geqslant C_{1}$
for an appropriate constant
![]() $C_{1}$
. In this case, by (3.5) and a linear transformation, we obtain the following estimate
$C_{1}$
. In this case, by (3.5) and a linear transformation, we obtain the following estimate
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{|t|\geqslant 1}\int _{\substack{ \unicode[STIX]{x1D70C}(x)\geqslant C_{0} \\ \unicode[STIX]{x1D70C}(x-\mathfrak{p}(t))\geqslant C_{1}}}|h_{z}(x-y-\mathfrak{p}(t))-h_{z}(x-\mathfrak{p}(t))|\nonumber\\ \displaystyle & & \displaystyle \qquad \times \log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx|t|^{\text{Re}(z)-k}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(z)\int _{|t|\geqslant 1}\int _{\substack{ \unicode[STIX]{x1D70C}(x)\geqslant C_{0} \\ \unicode[STIX]{x1D70C}(x-\mathfrak{p}(t))\geqslant C_{1}}}\frac{|y|}{\{\unicode[STIX]{x1D70C}(x-\mathfrak{p}(t))\}^{\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D707}+\text{Re}(z)}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx|t|^{\text{Re}(z)-k}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(z)\int _{|t|\geqslant 1}\int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{1}}\frac{1}{\{\unicode[STIX]{x1D70C}(x)\}^{\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D707}+\text{Re}(z)}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \log ^{N}(e+c\unicode[STIX]{x1D70C}(x)+ct)\,dx|t|^{\text{Re}(z)-k}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(z)\int _{|t|\geqslant 1}\int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{1}}\frac{1}{\{\unicode[STIX]{x1D70C}(x)\}^{\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D707}+\text{Re}(z)}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\{\log ^{N}(e+\unicode[STIX]{x1D70C}(x))+\log ^{N}(e+t)\}\,dx|t|^{\text{Re}(z)-k}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(z),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{|t|\geqslant 1}\int _{\substack{ \unicode[STIX]{x1D70C}(x)\geqslant C_{0} \\ \unicode[STIX]{x1D70C}(x-\mathfrak{p}(t))\geqslant C_{1}}}|h_{z}(x-y-\mathfrak{p}(t))-h_{z}(x-\mathfrak{p}(t))|\nonumber\\ \displaystyle & & \displaystyle \qquad \times \log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx|t|^{\text{Re}(z)-k}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(z)\int _{|t|\geqslant 1}\int _{\substack{ \unicode[STIX]{x1D70C}(x)\geqslant C_{0} \\ \unicode[STIX]{x1D70C}(x-\mathfrak{p}(t))\geqslant C_{1}}}\frac{|y|}{\{\unicode[STIX]{x1D70C}(x-\mathfrak{p}(t))\}^{\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D707}+\text{Re}(z)}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx|t|^{\text{Re}(z)-k}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(z)\int _{|t|\geqslant 1}\int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{1}}\frac{1}{\{\unicode[STIX]{x1D70C}(x)\}^{\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D707}+\text{Re}(z)}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \log ^{N}(e+c\unicode[STIX]{x1D70C}(x)+ct)\,dx|t|^{\text{Re}(z)-k}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(z)\int _{|t|\geqslant 1}\int _{\unicode[STIX]{x1D70C}(x)\geqslant C_{1}}\frac{1}{\{\unicode[STIX]{x1D70C}(x)\}^{\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D707}+\text{Re}(z)}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\{\log ^{N}(e+\unicode[STIX]{x1D70C}(x))+\log ^{N}(e+t)\}\,dx|t|^{\text{Re}(z)-k}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(z),\nonumber\end{eqnarray}$$
where we have used the fact that for fixed
![]() $|t|\geqslant 1$
,
$|t|\geqslant 1$
,
![]() $\unicode[STIX]{x1D70C}(x)\leqslant c[\unicode[STIX]{x1D70C}(x-\mathfrak{p}(t))+\unicode[STIX]{x1D70C}(\mathfrak{p}(t))]=c[\unicode[STIX]{x1D70C}(x-\mathfrak{p}(t))+t]$
.
$\unicode[STIX]{x1D70C}(x)\leqslant c[\unicode[STIX]{x1D70C}(x-\mathfrak{p}(t))+\unicode[STIX]{x1D70C}(\mathfrak{p}(t))]=c[\unicode[STIX]{x1D70C}(x-\mathfrak{p}(t))+t]$
.
It is trivial that
![]() $\unicode[STIX]{x1D70C}\big(x+y+\mathfrak{p}(t)\big)\leqslant c^{2}[\unicode[STIX]{x1D70C}(x)+\unicode[STIX]{x1D70C}(y)+\unicode[STIX]{x1D70C}(\mathfrak{p}(t))]=c^{2}[1+\unicode[STIX]{x1D70C}(x)+t]$
. Then, the remainder can be controlled by
$\unicode[STIX]{x1D70C}\big(x+y+\mathfrak{p}(t)\big)\leqslant c^{2}[\unicode[STIX]{x1D70C}(x)+\unicode[STIX]{x1D70C}(y)+\unicode[STIX]{x1D70C}(\mathfrak{p}(t))]=c^{2}[1+\unicode[STIX]{x1D70C}(x)+t]$
. Then, the remainder can be controlled by
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{|t|\geqslant 1}\int _{\substack{ \unicode[STIX]{x1D70C}(x)\geqslant C_{0} \\ \unicode[STIX]{x1D70C}(x-\mathfrak{p}(t))\leqslant C_{1}}}[|h_{z}(x-y-\mathfrak{p}(t))|+|h_{z}(x-\mathfrak{p}(t))|]\nonumber\\ \displaystyle & & \displaystyle \qquad \times \log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx|t|^{\text{Re}(z)-k}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{|t|\geqslant 1}\int _{\substack{ \unicode[STIX]{x1D70C}(x)\geqslant C_{0} \\ \unicode[STIX]{x1D70C}(x-\mathfrak{p}(t))\leqslant C_{1}}}|h_{z}(x-y-\mathfrak{p}(t))|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx|t|^{\text{Re}(z)-k}\,dt\nonumber\\ \displaystyle & & \displaystyle \qquad +\int _{|t|\geqslant 1}\int _{\substack{ \unicode[STIX]{x1D70C}(x)\geqslant C_{0} \\ \unicode[STIX]{x1D70C}(x-\mathfrak{p}(t))\leqslant C_{1}}}|h_{z}(x-\mathfrak{p}(t))|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx|t|^{\text{Re}(z)-k}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C\int _{|t|\geqslant 1}\int _{\substack{ \unicode[STIX]{x1D70C}(x)\leqslant c(C_{1}+1)}}|h_{z}(x)|\,dx|t|^{\text{Re}(z)-k}\log ^{N}(e+t)\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(z),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{|t|\geqslant 1}\int _{\substack{ \unicode[STIX]{x1D70C}(x)\geqslant C_{0} \\ \unicode[STIX]{x1D70C}(x-\mathfrak{p}(t))\leqslant C_{1}}}[|h_{z}(x-y-\mathfrak{p}(t))|+|h_{z}(x-\mathfrak{p}(t))|]\nonumber\\ \displaystyle & & \displaystyle \qquad \times \log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx|t|^{\text{Re}(z)-k}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{|t|\geqslant 1}\int _{\substack{ \unicode[STIX]{x1D70C}(x)\geqslant C_{0} \\ \unicode[STIX]{x1D70C}(x-\mathfrak{p}(t))\leqslant C_{1}}}|h_{z}(x-y-\mathfrak{p}(t))|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx|t|^{\text{Re}(z)-k}\,dt\nonumber\\ \displaystyle & & \displaystyle \qquad +\int _{|t|\geqslant 1}\int _{\substack{ \unicode[STIX]{x1D70C}(x)\geqslant C_{0} \\ \unicode[STIX]{x1D70C}(x-\mathfrak{p}(t))\leqslant C_{1}}}|h_{z}(x-\mathfrak{p}(t))|\log ^{N}(e+\unicode[STIX]{x1D70C}(x))\,dx|t|^{\text{Re}(z)-k}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C\int _{|t|\geqslant 1}\int _{\substack{ \unicode[STIX]{x1D70C}(x)\leqslant c(C_{1}+1)}}|h_{z}(x)|\,dx|t|^{\text{Re}(z)-k}\log ^{N}(e+t)\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(z),\nonumber\end{eqnarray}$$
where we have used the fact that
![]() $h_{z}$
is locally integrable.
$h_{z}$
is locally integrable.
3.3 Analytic interpolation
To complete the proof of (2.1), we use a vector-valued extension of Stein interpolation theorem [Reference Stein15].
Note that
![]() $\mathbf{X}=[\mathbf{H},\mathbf{Y}]_{\unicode[STIX]{x1D703}}$
for some Hilbert space
$\mathbf{X}=[\mathbf{H},\mathbf{Y}]_{\unicode[STIX]{x1D703}}$
for some Hilbert space
![]() $\mathbf{H}$
, UMD space
$\mathbf{H}$
, UMD space
![]() $\mathbf{Y}$
and
$\mathbf{Y}$
and
![]() $\unicode[STIX]{x1D703}\in (0,1)$
. For fixed
$\unicode[STIX]{x1D703}\in (0,1)$
. For fixed
![]() $\mathbf{H}$
and
$\mathbf{H}$
and
![]() $\mathbf{Y}$
, there exists a constant
$\mathbf{Y}$
, there exists a constant
![]() $C(z)$
growing at most polynomially in
$C(z)$
growing at most polynomially in
![]() $(1+|\text{Im}(z)|)$
such that
$(1+|\text{Im}(z)|)$
such that
and
Obviously, (3.7) also holds in particular with
![]() $\mathbf{Y}=\mathbf{H}$
.
$\mathbf{Y}=\mathbf{H}$
.
For
![]() $1<p<\infty$
, we chose
$1<p<\infty$
, we chose
![]() $\unicode[STIX]{x1D703}_{1}\in (0,1)$
,
$\unicode[STIX]{x1D703}_{1}\in (0,1)$
,
![]() $0<\unicode[STIX]{x1D70E}_{0}<\frac{1}{d}$
,
$0<\unicode[STIX]{x1D70E}_{0}<\frac{1}{d}$
,
![]() $-\unicode[STIX]{x1D6FD}<\unicode[STIX]{x1D70E}_{1}<0$
and
$-\unicode[STIX]{x1D6FD}<\unicode[STIX]{x1D70E}_{1}<0$
and
![]() $q_{1}\in (1,\infty )$
such that
$q_{1}\in (1,\infty )$
such that
Interpolating between (3.6) and (3.7) with
![]() $\mathbf{Y}$
replaced by
$\mathbf{Y}$
replaced by
![]() $\mathbf{H}$
, we have
$\mathbf{H}$
, we have
For fixed
![]() $\unicode[STIX]{x1D703}$
, we choose
$\unicode[STIX]{x1D703}$
, we choose
![]() $-\unicode[STIX]{x1D6FD}<\unicode[STIX]{x1D70E}_{3}<0$
such that
$-\unicode[STIX]{x1D6FD}<\unicode[STIX]{x1D70E}_{3}<0$
such that
![]() $0=(1-\unicode[STIX]{x1D703})\unicode[STIX]{x1D70E}_{2}+\unicode[STIX]{x1D703}\unicode[STIX]{x1D70E}_{3}$
. In the same way, interpolating between (3.8) and (3.7) with
$0=(1-\unicode[STIX]{x1D703})\unicode[STIX]{x1D70E}_{2}+\unicode[STIX]{x1D703}\unicode[STIX]{x1D70E}_{3}$
. In the same way, interpolating between (3.8) and (3.7) with
![]() $q=p$
, we obtain
$q=p$
, we obtain
This completes the proof of (2.1).