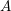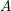1 Introduction
1.1 Background
Quasi-hereditary algebras were introduced by Scott [Reference Scott23] to study highest weight categories in the representation theory of semisimple complex Lie algebras and algebraic groups. Cline, Parshall and Scott proved many important results in [Reference Cline, Parshall and Scott5, Reference Parshall and Scott20]. Ringel introduced a special class of quasi-hereditary algebras called right-strongly quasi-hereditary algebras [Reference Ringel22], motivated by Iyama’s finiteness theorem of representation dimensions of artin algebras [Reference Iyama16, Reference Iyama17]. One of the advantages of right-strongly quasi-hereditary algebras is that they have better upper bound of global dimension than that of general quasi-hereditary algebras [Reference Ringel22, Section 4]. By [Reference Iyama16], it follows that any artin algebra
![]() $A$
can be written as
$A$
can be written as
![]() $eBe$
for some right-strongly quasi-hereditary algebra
$eBe$
for some right-strongly quasi-hereditary algebra
![]() $B$
and an idempotent
$B$
and an idempotent
![]() $e$
of
$e$
of
![]() $B$
. This idea is widely applicable and hence right-strongly quasi-hereditary algebras appear in the representation theory frequently. Also certain important algebras associated with preprojective algebras and elements in Coxeter groups are known to be right-strongly quasi-hereditary, e.g., [Reference Geiss, Leclerc and Schröer15, Reference Iyama and Reiten19]. We refer to [Reference Conde6, Reference Conde7, Reference Eiríksson13] for recent results on right-strongly quasi-hereditary algebras.
$B$
. This idea is widely applicable and hence right-strongly quasi-hereditary algebras appear in the representation theory frequently. Also certain important algebras associated with preprojective algebras and elements in Coxeter groups are known to be right-strongly quasi-hereditary, e.g., [Reference Geiss, Leclerc and Schröer15, Reference Iyama and Reiten19]. We refer to [Reference Conde6, Reference Conde7, Reference Eiríksson13] for recent results on right-strongly quasi-hereditary algebras.
In this paper, we discuss categorical aspects of right-strongly quasi-hereditary algebras following an approach in [Reference Iyama17, Section 2], which is unpublished. In particular, we give a characterization of right-strongly quasi-hereditary algebras in terms of the following three notions (Theorem 3.33).
∙ right-strongly heredity chains (Definition 3.1),
∙ total right rejective chains (Definition 3.19),
∙ coreflective chains (Definition 3.31).
As application, we sharpen a well-known result of Dlab and Ringel [Reference Dlab and Ringel9, Theorem 2] stating that any artin algebra of global dimension at most two is quasi-hereditary. We prove that such an algebra is always right-strongly (resp. left-strongly) quasi-hereditary (Theorem 4.1). We give a detailed proof following the strategy of [Reference Iyama17, Theorem 3.6]. Moreover we show that the Auslander algebra of a representation-finite algebra
![]() $A$
is strongly quasi-hereditary if and only if
$A$
is strongly quasi-hereditary if and only if
![]() $A$
is a Nakayama algebra.
$A$
is a Nakayama algebra.
1.2 Our results
Recall that right-strongly (resp. left-strongly) quasi-hereditary algebras are defined as quasi-hereditary algebras whose standard modules have projective dimension at most one (Definition 2.5). Our starting point is the following observation which gives a characterization of right-strongly (resp. left-strongly) quasi-hereditary algebras in terms of heredity chains.
Proposition 1.1. (Proposition 3.7)
Let
![]() $A$
be an artin algebra. Then
$A$
be an artin algebra. Then
![]() $A$
is right-strongly (resp. left-strongly) quasi-hereditary if and only if there exists a heredity chain
$A$
is right-strongly (resp. left-strongly) quasi-hereditary if and only if there exists a heredity chain
such that
![]() $H_{i}$
is a projective right (resp. left)
$H_{i}$
is a projective right (resp. left)
![]() $A$
-module for any
$A$
-module for any
![]() $0\leqslant i\leqslant n-1$
.
$0\leqslant i\leqslant n-1$
.
We call such a heredity chain a right-strongly (resp. left-strongly) heredity chain.
Moreover we give categorical interpretations of right-strongly (resp. left-strongly) heredity chains. For an artin algebra
![]() $A$
, there exists a bijection between idempotent ideals of
$A$
, there exists a bijection between idempotent ideals of
![]() $A$
and full subcategories of the category
$A$
and full subcategories of the category
![]() $\mathsf{proj}A$
of finitely generated projective
$\mathsf{proj}A$
of finitely generated projective
![]() $A$
-modules given by
$A$
-modules given by
![]() $AeA\mapsto \mathsf{add}eA$
. This gives a bijection between chains of idempotent ideals of
$AeA\mapsto \mathsf{add}eA$
. This gives a bijection between chains of idempotent ideals of
![]() $A$
and chains of full subcategories of
$A$
and chains of full subcategories of
![]() $\mathsf{proj}A$
. A key idea of this paper is to translate properties of idempotent ideals into properties of full subcategories of
$\mathsf{proj}A$
. A key idea of this paper is to translate properties of idempotent ideals into properties of full subcategories of
![]() $\mathsf{proj}A$
.
$\mathsf{proj}A$
.
For an artin algebra
![]() $A$
and an arbitrary factor algebra
$A$
and an arbitrary factor algebra
![]() $B$
of
$B$
of
![]() $A$
, we naturally regard
$A$
, we naturally regard
![]() $\mathsf{mod}B$
as a full subcategory of
$\mathsf{mod}B$
as a full subcategory of
![]() $\mathsf{mod}A$
. In this case, each
$\mathsf{mod}A$
. In this case, each
![]() $X\in \mathsf{mod}A$
has a right (resp. left)
$X\in \mathsf{mod}A$
has a right (resp. left)
![]() $(\mathsf{mod}B)$
-approximation of
$(\mathsf{mod}B)$
-approximation of
![]() $X$
which is monic (resp. epic) in
$X$
which is monic (resp. epic) in
![]() $\mathsf{mod}A$
. More generally, subcategories of an additive category with these properties are called right (resp. left) rejective in [Reference Iyama17, Reference Iyama18]. They are a special class of coreflective (resp. reflective) subcategories (see Definition 3.27) appearing in the classical theory of localizations of abelian categories [Reference Stenström24].
$\mathsf{mod}A$
. More generally, subcategories of an additive category with these properties are called right (resp. left) rejective in [Reference Iyama17, Reference Iyama18]. They are a special class of coreflective (resp. reflective) subcategories (see Definition 3.27) appearing in the classical theory of localizations of abelian categories [Reference Stenström24].
Using the notion of right rejective (resp. left rejective, coreflective, reflective) subcategories, we introduce the notion of total right rejective (resp. total left rejective, coreflective, reflective) chains of an additive category (Definitions 3.19, 3.31). The following main theorem in this paper characterizes right-strongly (resp. left-strongly) quasi-hereditary algebras in terms of these chains.
Theorem 1.2. (Theorems 3.22 and 3.33)
Let
![]() $A$
be an artin algebra and
$A$
be an artin algebra and
a chain of idempotent ideals of
![]() $A$
. For
$A$
. For
![]() $0\leqslant i\leqslant n-1$
, we write
$0\leqslant i\leqslant n-1$
, we write
![]() $H_{i}=Ae_{i}A$
, where
$H_{i}=Ae_{i}A$
, where
![]() $e_{i}$
is an idempotent of
$e_{i}$
is an idempotent of
![]() $A$
. Then the following conditions are equivalent:
$A$
. Then the following conditions are equivalent:
(i) (1.1) is a right-strongly (resp. left-strongly) heredity chain.
(ii) The following chain is a total right (resp. left) rejective chain of
 $\mathsf{proj}A$
.
$\mathsf{proj}A$
.  $$\begin{eqnarray}\mathsf{proj}A=\mathsf{add}e_{0}A\supset \mathsf{add}e_{1}A\supset \cdots \supset \mathsf{add}e_{n}A=0.\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{proj}A=\mathsf{add}e_{0}A\supset \mathsf{add}e_{1}A\supset \cdots \supset \mathsf{add}e_{n}A=0.\end{eqnarray}$$
(iii) (1.1) is a heredity chain of
 $A$
and the following chain is a coreflective (resp. reflective) chain of
$A$
and the following chain is a coreflective (resp. reflective) chain of
 $\mathsf{proj}A$
.
$\mathsf{proj}A$
.  $$\begin{eqnarray}\mathsf{proj}A=\mathsf{add}e_{0}A\supset \mathsf{add}e_{1}A\supset \cdots \supset \mathsf{add}e_{n}A=0.\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{proj}A=\mathsf{add}e_{0}A\supset \mathsf{add}e_{1}A\supset \cdots \supset \mathsf{add}e_{n}A=0.\end{eqnarray}$$
We apply total right (resp. left) rejective chains to study right-strongly (resp. left-strongly) quasi-hereditary algebras. We give the following result by combining [Reference Iyama17, Theorem 3.6] and Theorem 1.2.
Theorem 1.3. (Theorem 4.1)
Let
![]() $A$
be an artin algebra. If
$A$
be an artin algebra. If
![]() $\operatorname{gldim}A\leqslant 2$
, then
$\operatorname{gldim}A\leqslant 2$
, then
![]() $A$
is a right-strongly (resp. left-strongly) quasi-hereditary algebra.
$A$
is a right-strongly (resp. left-strongly) quasi-hereditary algebra.
An artin algebra which has a heredity chain such that it is a right-strongly heredity chain and a left-strongly heredity chain is called a strongly quasi-hereditary algebra. They have global dimension at most two [Reference Ringel22], but algebras with global dimension at most two are not necessarily strongly quasi-hereditary. Applying our results on rejective chains, we give the following characterization of Auslander algebras to be strongly quasi-hereditary.
Theorem 1.4. (Theorem 4.6)
Let
![]() $A$
be a representation-finite artin algebra and
$A$
be a representation-finite artin algebra and
![]() $B$
the Auslander algebra of
$B$
the Auslander algebra of
![]() $A$
. Then
$A$
. Then
![]() $B$
is a strongly quasi-hereditary algebra if and only if
$B$
is a strongly quasi-hereditary algebra if and only if
![]() $A$
is a Nakayama algebra (see [Reference Auslander, Reiten and Smalø3, Section 4.2] for the definition of Nakayama algebras).
$A$
is a Nakayama algebra (see [Reference Auslander, Reiten and Smalø3, Section 4.2] for the definition of Nakayama algebras).
Note that Theorem 1.4 can be deduced from a recent result [Reference Eiríksson13, Theorem 3], which is shown by a different method.
2 Preliminaries
Notation. For background materials in representation theory of algebras, we refer to [Reference Assem, Simson and Skowroński1, Reference Auslander, Reiten and Smalø3]. Let
![]() $A$
be an artin algebra. Let
$A$
be an artin algebra. Let
![]() $J(A)$
be the Jacobson radical of
$J(A)$
be the Jacobson radical of
![]() $A$
. We denote by
$A$
. We denote by
![]() $\operatorname{gldim}A$
the global dimension of
$\operatorname{gldim}A$
the global dimension of
![]() $A$
. We write
$A$
. We write
![]() $\mathsf{mod}A$
for the category of finitely generated right
$\mathsf{mod}A$
for the category of finitely generated right
![]() $A$
-modules and
$A$
-modules and
![]() $\mathsf{proj}A$
for the full subcategory of
$\mathsf{proj}A$
for the full subcategory of
![]() $\mathsf{mod}A$
consisting of the finitely generated projective
$\mathsf{mod}A$
consisting of the finitely generated projective
![]() $A$
-modules. For
$A$
-modules. For
![]() $M\in \mathsf{mod}A$
, we denote by
$M\in \mathsf{mod}A$
, we denote by
![]() $\mathsf{add}M$
the full subcategory of
$\mathsf{add}M$
the full subcategory of
![]() $\mathsf{mod}A$
whose objects are direct summands of finite direct sums of copies of
$\mathsf{mod}A$
whose objects are direct summands of finite direct sums of copies of
![]() $M$
.
$M$
.
We fix a complete set of representatives of isomorphism classes of simple
![]() $A$
-modules
$A$
-modules
![]() $\{S(i)\mid i\in I\}$
. For
$\{S(i)\mid i\in I\}$
. For
![]() $i\in I$
, we denote by
$i\in I$
, we denote by
![]() $P(i)$
the projective cover of
$P(i)$
the projective cover of
![]() $S(i)$
. For
$S(i)$
. For
![]() $X\in \mathsf{mod}A$
, we write
$X\in \mathsf{mod}A$
, we write
![]() $[X:S(i)]$
for the composition multiplicity of
$[X:S(i)]$
for the composition multiplicity of
![]() $S(i)$
. We denote by
$S(i)$
. We denote by
![]() $\mathbf{k}$
a field.
$\mathbf{k}$
a field.
2.1 Quasi-hereditary algebras and highest weight categories
We start with recalling definitions of quasi-hereditary algebras and highest weight categories.
Definition 2.1. (Cline–Parshall–Scott [Reference Cline, Parshall and Scott5], Dlab–Ringel [Reference Dlab and Ringel9])
Let
![]() $A$
be an artin algebra.
$A$
be an artin algebra.
(1) A two-sided ideal
 $H$
of
$H$
of
 $A$
is called heredity if it satisfies the following conditions:
$A$
is called heredity if it satisfies the following conditions:(a)
 $H$
is an idempotent ideal (i.e.,
$H$
is an idempotent ideal (i.e.,
 $H^{2}=H$
), or equivalently, there exists an idempotent
$H^{2}=H$
), or equivalently, there exists an idempotent
 $e$
such that
$e$
such that
 $H=AeA$
[Reference Dlab and Ringel9, Statement 6];
$H=AeA$
[Reference Dlab and Ringel9, Statement 6];(b)
 $H$
is projective as a right
$H$
is projective as a right
 $A$
-module;
$A$
-module;(c)
 $HJ(A)H=0$
.
$HJ(A)H=0$
.
(2) A chain of idempotent ideals of
 $A$
is called a heredity chain if
$A$
is called a heredity chain if $$\begin{eqnarray}A=H_{0}>H_{1}>\cdots >H_{i}>H_{i+1}>\cdots >H_{n}=0\end{eqnarray}$$
$$\begin{eqnarray}A=H_{0}>H_{1}>\cdots >H_{i}>H_{i+1}>\cdots >H_{n}=0\end{eqnarray}$$
 $H_{i}/H_{i+1}$
is a heredity ideal of
$H_{i}/H_{i+1}$
is a heredity ideal of
 $A/H_{i+1}$
for
$A/H_{i+1}$
for
 $0\leqslant i\leqslant n-1$
.
$0\leqslant i\leqslant n-1$
.(3)
 $A$
is called a quasi-hereditary algebra if there exists a heredity chain of
$A$
is called a quasi-hereditary algebra if there exists a heredity chain of
 $A$
.
$A$
.
Quasi-hereditary algebras are strongly related to highest weight categories defined below. In fact, an artin algebra
![]() $A$
is quasi-hereditary if and only if
$A$
is quasi-hereditary if and only if
![]() $\mathsf{mod}A$
is a highest weight category [Reference Cline, Parshall and Scott5, Theorem 3.6].
$\mathsf{mod}A$
is a highest weight category [Reference Cline, Parshall and Scott5, Theorem 3.6].
Let
![]() ${\leqslant}$
be a partial order on the index set
${\leqslant}$
be a partial order on the index set
![]() $I$
of simple
$I$
of simple
![]() $A$
-modules. For each
$A$
-modules. For each
![]() $i\in I$
, we denote by
$i\in I$
, we denote by
![]() $\unicode[STIX]{x1D6E5}(i)$
the maximal factor module of
$\unicode[STIX]{x1D6E5}(i)$
the maximal factor module of
![]() $P(i)$
whose composition factors have the form
$P(i)$
whose composition factors have the form
![]() $S(j)$
, for some
$S(j)$
, for some
![]() $j\leqslant i$
. The module
$j\leqslant i$
. The module
![]() $\unicode[STIX]{x1D6E5}(i)$
is called the standard module corresponding to
$\unicode[STIX]{x1D6E5}(i)$
is called the standard module corresponding to
![]() $i$
. Let
$i$
. Let
![]() $\unicode[STIX]{x1D6E5}:=\{\unicode[STIX]{x1D6E5}(i)\mid i\in I\}$
be the set of standard modules. We denote by
$\unicode[STIX]{x1D6E5}:=\{\unicode[STIX]{x1D6E5}(i)\mid i\in I\}$
be the set of standard modules. We denote by
![]() ${\mathcal{F}}(\unicode[STIX]{x1D6E5})$
the full subcategory of
${\mathcal{F}}(\unicode[STIX]{x1D6E5})$
the full subcategory of
![]() $\mathsf{mod}A$
whose objects are the modules which have a
$\mathsf{mod}A$
whose objects are the modules which have a
![]() $\unicode[STIX]{x1D6E5}$
-filtration, namely
$\unicode[STIX]{x1D6E5}$
-filtration, namely
![]() $M\in {\mathcal{F}}(\unicode[STIX]{x1D6E5})$
if and only if there exists a chain of submodules
$M\in {\mathcal{F}}(\unicode[STIX]{x1D6E5})$
if and only if there exists a chain of submodules
such that
![]() $M_{i}/M_{i+1}$
is isomorphic to a module in
$M_{i}/M_{i+1}$
is isomorphic to a module in
![]() $\unicode[STIX]{x1D6E5}$
. For
$\unicode[STIX]{x1D6E5}$
. For
![]() $M\in {\mathcal{F}}(\unicode[STIX]{x1D6E5})$
, we denote by
$M\in {\mathcal{F}}(\unicode[STIX]{x1D6E5})$
, we denote by
![]() $(M:\unicode[STIX]{x1D6E5}(i))$
the filtration multiplicity of
$(M:\unicode[STIX]{x1D6E5}(i))$
the filtration multiplicity of
![]() $\unicode[STIX]{x1D6E5}(i)$
, which dose not depend on the choice of
$\unicode[STIX]{x1D6E5}(i)$
, which dose not depend on the choice of
![]() $\unicode[STIX]{x1D6E5}$
-filtrations (cf. [Reference Donkin11, A.1 (7)]).
$\unicode[STIX]{x1D6E5}$
-filtrations (cf. [Reference Donkin11, A.1 (7)]).
Definition 2.2. (Cline–Parshall–Scott [Reference Cline, Parshall and Scott5])
We say that a pair
![]() $(\mathsf{mod}A,\leqslant )$
is a highest weight category if there exists a short exact sequence
$(\mathsf{mod}A,\leqslant )$
is a highest weight category if there exists a short exact sequence
for any
![]() $i\in I$
with the following properties:
$i\in I$
with the following properties:
(a)
 $K(i)\in {\mathcal{F}}(\unicode[STIX]{x1D6E5})$
for any
$K(i)\in {\mathcal{F}}(\unicode[STIX]{x1D6E5})$
for any
 $i\in I$
;
$i\in I$
;(b) if
 $(K(i):\unicode[STIX]{x1D6E5}(j))\not =0$
, then we have
$(K(i):\unicode[STIX]{x1D6E5}(j))\not =0$
, then we have
 $i<j$
.
$i<j$
.
For a highest weight category
![]() $(\mathsf{mod}A,\leqslant )$
and a refinement
$(\mathsf{mod}A,\leqslant )$
and a refinement
![]() ${\leqslant}^{\prime }$
of
${\leqslant}^{\prime }$
of
![]() ${\leqslant}$
, it is clear that
${\leqslant}$
, it is clear that
![]() $(\mathsf{mod}A,\leqslant ^{\prime })$
is also a highest weight category whose standard modules coincide with those of
$(\mathsf{mod}A,\leqslant ^{\prime })$
is also a highest weight category whose standard modules coincide with those of
![]() $(\mathsf{mod}A,\leqslant )$
. Therefore, without loss of generality, one can assume that the partial order
$(\mathsf{mod}A,\leqslant )$
. Therefore, without loss of generality, one can assume that the partial order
![]() ${\leqslant}$
on
${\leqslant}$
on
![]() $I$
is a total order.
$I$
is a total order.
To explain a connection between quasi-hereditary algebras and highest weight categories more explicitly, we introduce the following notion.
Definition 2.3. (Uematsu–Yamagata [Reference Uematsu and Yamagata25])
Let
![]() $A$
be an artin algebra. A chain of idempotent ideals
$A$
be an artin algebra. A chain of idempotent ideals
is called maximal if the length of the chain is the number of simple modules.
Any heredity chain of an artin algebra can be refined to a maximal heredity chain [Reference Uematsu and Yamagata25, Proposition 1.3].
Let
![]() $A$
be an artin algebra with simple
$A$
be an artin algebra with simple
![]() $A$
-modules
$A$
-modules
![]() $\{S(i)\mid i\in I\}$
and
$\{S(i)\mid i\in I\}$
and
![]() $e_{i}$
a primitive idempotent of
$e_{i}$
a primitive idempotent of
![]() $A$
corresponding to
$A$
corresponding to
![]() $S(i)$
. Then there is a bijection
$S(i)$
. Then there is a bijection
given by setting
![]() $H_{j}:=A(e_{i_{j+1}}+\cdots +e_{i_{n}})A$
and
$H_{j}:=A(e_{i_{j+1}}+\cdots +e_{i_{n}})A$
and
Proposition 2.4. (Cline–Parshall–Scott [Reference Cline, Parshall and Scott5, Section 3])
Let
![]() $A$
be an artin algebra and
$A$
be an artin algebra and
![]() ${\leqslant}$
a total order on
${\leqslant}$
a total order on
![]() $I$
.
$I$
.
(1) A pair
 $(\mathsf{mod}A,\leqslant )$
is a highest weight category with standard modules
$(\mathsf{mod}A,\leqslant )$
is a highest weight category with standard modules
 $\{\unicode[STIX]{x1D6E5}(i_{1}),\ldots ,\unicode[STIX]{x1D6E5}(i_{n})\}$
if and only if the corresponding maximal chain of idempotent ideals is a heredity chain.
$\{\unicode[STIX]{x1D6E5}(i_{1}),\ldots ,\unicode[STIX]{x1D6E5}(i_{n})\}$
if and only if the corresponding maximal chain of idempotent ideals is a heredity chain.(2) If the condition in
 $(1)$
is satisfied, then we have
$(1)$
is satisfied, then we have
 $H_{j}/H_{j+1}\cong \unicode[STIX]{x1D6E5}(i_{j})^{m_{j}}$
as right
$H_{j}/H_{j+1}\cong \unicode[STIX]{x1D6E5}(i_{j})^{m_{j}}$
as right
 $A$
-modules for some positive integer
$A$
-modules for some positive integer
 $m_{j}$
.
$m_{j}$
.
2.2 Right-strongly (resp. left-strongly) quasi-hereditary algebras
Now, we recall the following special class of quasi-hereditary algebras.
Definition 2.5. (Ringel [Reference Ringel22, Section 4])
Let
![]() $A$
be an artin algebra and
$A$
be an artin algebra and
![]() ${\leqslant}$
a partial order on
${\leqslant}$
a partial order on
![]() $I$
.
$I$
.
(1) We say that a pair
 $(A,\leqslant )$
(or simply
$(A,\leqslant )$
(or simply
 $A$
) is right-strongly quasi-hereditary if there exists a short exact sequence for any
$A$
) is right-strongly quasi-hereditary if there exists a short exact sequence for any $$\begin{eqnarray}0\rightarrow K(i)\rightarrow P(i)\rightarrow \unicode[STIX]{x1D6E5}(i)\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow K(i)\rightarrow P(i)\rightarrow \unicode[STIX]{x1D6E5}(i)\rightarrow 0\end{eqnarray}$$
 $i\in I$
with the following properties:
$i\in I$
with the following properties:(a)
 $K(i)\in {\mathcal{F}}(\unicode[STIX]{x1D6E5})$
for all
$K(i)\in {\mathcal{F}}(\unicode[STIX]{x1D6E5})$
for all
 $i\in I$
;
$i\in I$
;(b) if
 $(K(i):\unicode[STIX]{x1D6E5}(j))\not =0$
, then we have
$(K(i):\unicode[STIX]{x1D6E5}(j))\not =0$
, then we have
 $i<j$
;
$i<j$
;(c)
 $K(i)$
is a projective right
$K(i)$
is a projective right
 $A$
-module, or equivalently the right
$A$
-module, or equivalently the right
 $A$
-module
$A$
-module
 $\unicode[STIX]{x1D6E5}(i)$
has projective dimension at most one.
$\unicode[STIX]{x1D6E5}(i)$
has projective dimension at most one.
(2) We say that a pair
 $(A,\leqslant )$
(or simply
$(A,\leqslant )$
(or simply
 $A$
) is left-strongly quasi-hereditary if
$A$
) is left-strongly quasi-hereditary if
 $(A^{\operatorname{op}},\leqslant )$
is right-strongly quasi-hereditary.
$(A^{\operatorname{op}},\leqslant )$
is right-strongly quasi-hereditary.
Note that Definition 2.5 is slightly different from Ringel’s original definition (see [Reference Ringel22, Section 4]). We can easily check that these are equivalent to each other. Indeed, his definition induces our conditions (a) and (b) because the pair
![]() $(\mathsf{mod}A,\leqslant )$
is a highest weight category by [Reference Ringel22, Section 4, Proposition]. Moreover, his condition (a) clearly gives our condition (c). Conversely, his condition (a) follows from our conditions (a) and (c). Furthermore, our conditions (a) and (b) induce his condition (b).
$(\mathsf{mod}A,\leqslant )$
is a highest weight category by [Reference Ringel22, Section 4, Proposition]. Moreover, his condition (a) clearly gives our condition (c). Conversely, his condition (a) follows from our conditions (a) and (c). Furthermore, our conditions (a) and (b) induce his condition (b).
As before, for a right-strongly quasi-hereditary algebra
![]() $(A,\leqslant )$
and a refinement
$(A,\leqslant )$
and a refinement
![]() ${\leqslant}^{\prime }$
of
${\leqslant}^{\prime }$
of
![]() ${\leqslant}$
, it is clear that
${\leqslant}$
, it is clear that
![]() $(A,\leqslant ^{\prime })$
is also a right-strongly quasi-hereditary algebra whose standard modules coincide with those of
$(A,\leqslant ^{\prime })$
is also a right-strongly quasi-hereditary algebra whose standard modules coincide with those of
![]() $(A,\leqslant )$
. Therefore, without loss of generality, one can assume that the partial order
$(A,\leqslant )$
. Therefore, without loss of generality, one can assume that the partial order
![]() ${\leqslant}$
on
${\leqslant}$
on
![]() $I$
is a total order.
$I$
is a total order.
In this paper, for a quiver
![]() $Q$
and arrows
$Q$
and arrows
![]() $\unicode[STIX]{x1D6FC}:x\rightarrow y$
and
$\unicode[STIX]{x1D6FC}:x\rightarrow y$
and
![]() $\unicode[STIX]{x1D6FD}:y\rightarrow z$
in
$\unicode[STIX]{x1D6FD}:y\rightarrow z$
in
![]() $Q$
, we denote by
$Q$
, we denote by
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}$
the composition.
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}$
the composition.
Example 2.6. We assume that a natural number
![]() $n$
is at least two. Let
$n$
is at least two. Let
![]() $A_{n}$
be the
$A_{n}$
be the
![]() $\mathbf{k}$
-algebra defined by the quiver
$\mathbf{k}$
-algebra defined by the quiver
with relations
![]() $\unicode[STIX]{x1D6FC}_{i-1}\unicode[STIX]{x1D6FC}_{i}$
,
$\unicode[STIX]{x1D6FC}_{i-1}\unicode[STIX]{x1D6FC}_{i}$
,
![]() $\unicode[STIX]{x1D6FD}_{i}\unicode[STIX]{x1D6FD}_{i-1}$
,
$\unicode[STIX]{x1D6FD}_{i}\unicode[STIX]{x1D6FD}_{i-1}$
,
![]() $\unicode[STIX]{x1D6FD}_{i-1}\unicode[STIX]{x1D6FC}_{i-1}-\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D6FD}_{i}$
for
$\unicode[STIX]{x1D6FD}_{i-1}\unicode[STIX]{x1D6FC}_{i-1}-\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D6FD}_{i}$
for
![]() $2\leqslant i\leqslant n-1$
and
$2\leqslant i\leqslant n-1$
and
![]() $\unicode[STIX]{x1D6FD}_{n-1}\unicode[STIX]{x1D6FC}_{n-1}.$
The algebra
$\unicode[STIX]{x1D6FD}_{n-1}\unicode[STIX]{x1D6FC}_{n-1}.$
The algebra
![]() $A_{n}$
is Morita equivalent to a block of a Schur algebra (see [Reference Donkin and Reiten12, Reference Erdmann14]).
$A_{n}$
is Morita equivalent to a block of a Schur algebra (see [Reference Donkin and Reiten12, Reference Erdmann14]).
If
![]() $n=2$
, then the indecomposable projective modules
$n=2$
, then the indecomposable projective modules
![]() $P(i)$
have the following shape:
$P(i)$
have the following shape:
For the total order
![]() $\{1<2\}$
, we have
$\{1<2\}$
, we have
![]() $\unicode[STIX]{x1D6E5}(1)=S(1)$
and
$\unicode[STIX]{x1D6E5}(1)=S(1)$
and
![]() $\unicode[STIX]{x1D6E5}(2)=P(2)$
, and hence
$\unicode[STIX]{x1D6E5}(2)=P(2)$
, and hence
![]() $A_{2}$
is right-strongly quasi-hereditary.
$A_{2}$
is right-strongly quasi-hereditary.
If
![]() $n>2$
, then the indecomposable projective modules
$n>2$
, then the indecomposable projective modules
![]() $P(i)$
have the following shape:
$P(i)$
have the following shape:
Thus
![]() $A_{n}$
is quasi-hereditary with respect to the total order
$A_{n}$
is quasi-hereditary with respect to the total order
![]() $\{1<2<\cdots <n\}$
. However
$\{1<2<\cdots <n\}$
. However
![]() $A_{n}$
is not right-strongly quasi-hereditary with respect to any order.
$A_{n}$
is not right-strongly quasi-hereditary with respect to any order.
It is well known that a pair
![]() $(A,\leqslant )$
is quasi-hereditary if and only if so is
$(A,\leqslant )$
is quasi-hereditary if and only if so is
![]() $(A^{\operatorname{op}},\leqslant )$
(see [Reference Cline, Parshall and Scott5, Lemma 3.4] and [Reference Dlab and Ringel9, Statement 9]). However even if
$(A^{\operatorname{op}},\leqslant )$
(see [Reference Cline, Parshall and Scott5, Lemma 3.4] and [Reference Dlab and Ringel9, Statement 9]). However even if
![]() $(A,\leqslant )$
is right-strongly quasi-hereditary, it dose not necessarily hold that
$(A,\leqslant )$
is right-strongly quasi-hereditary, it dose not necessarily hold that
![]() $(A,\leqslant )$
is left-strongly quasi-hereditary. Moreover there is an example of a left-strongly quasi-hereditary algebra
$(A,\leqslant )$
is left-strongly quasi-hereditary. Moreover there is an example of a left-strongly quasi-hereditary algebra
![]() $A$
which is not right-strongly quasi-hereditary for any order on
$A$
which is not right-strongly quasi-hereditary for any order on
![]() $I$
(see [Reference Ringel22, A2(1)]).
$I$
(see [Reference Ringel22, A2(1)]).
Example 2.7. Let
![]() $B$
be the
$B$
be the
![]() $\mathbf{k}$
-algebra defined by the quiver
$\mathbf{k}$
-algebra defined by the quiver

with relations
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}$
,
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}$
,
![]() $\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}$
. Then the indecomposable projective
$\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}$
. Then the indecomposable projective
![]() $B$
-modules
$B$
-modules
![]() $P(i)$
have the following shape:
$P(i)$
have the following shape:
For the total order
![]() $\{1<2<3\}$
, we have
$\{1<2<3\}$
, we have
![]() $\unicode[STIX]{x1D6E5}(1)=S(1)$
and
$\unicode[STIX]{x1D6E5}(1)=S(1)$
and
![]() $\unicode[STIX]{x1D6E5}(i)=P(i)$
for
$\unicode[STIX]{x1D6E5}(i)=P(i)$
for
![]() $i=2,3$
, and hence
$i=2,3$
, and hence
![]() $B$
is right-strongly quasi-hereditary. On the other hand, the indecomposable projective
$B$
is right-strongly quasi-hereditary. On the other hand, the indecomposable projective
![]() $B^{\operatorname{op}}$
-modules have the following shape:
$B^{\operatorname{op}}$
-modules have the following shape:
For the total order
![]() $\{1<2<3\}$
, we have
$\{1<2<3\}$
, we have
![]() $\unicode[STIX]{x1D6E5}^{\operatorname{op}}(i)=S^{\operatorname{op}}(i)$
for
$\unicode[STIX]{x1D6E5}^{\operatorname{op}}(i)=S^{\operatorname{op}}(i)$
for
![]() $i=1,2$
and
$i=1,2$
and
![]() $\unicode[STIX]{x1D6E5}^{\operatorname{op}}(3)=P^{\operatorname{op}}(3)$
, and hence
$\unicode[STIX]{x1D6E5}^{\operatorname{op}}(3)=P^{\operatorname{op}}(3)$
, and hence
![]() $B$
is not left-strongly quasi-hereditary. However, for the total order
$B$
is not left-strongly quasi-hereditary. However, for the total order
![]() $\{2<1<3\}$
,
$\{2<1<3\}$
,
![]() $B$
is not right-strongly quasi-hereditary but
$B$
is not right-strongly quasi-hereditary but
![]() $B$
is left-strongly quasi-hereditary.
$B$
is left-strongly quasi-hereditary.
3 Characterizations of right-strongly quasi-hereditary algebras
3.1 Right-strongly heredity chains
In this subsection, we give a characterization of right-strongly (resp. left-strongly) quasi-hereditary algebras in terms of heredity chains.
Definition 3.1. Let
![]() $A$
be an artin algebra and
$A$
be an artin algebra and
a chain of idempotent ideals.
(1) We call (3.3) a right-strongly (resp. left-strongly) heredity chain if the following conditions hold for any
 $0\leqslant i\leqslant n-1$
:
$0\leqslant i\leqslant n-1$
:(a)
 $H_{i}$
is projective as a right (resp. left)
$H_{i}$
is projective as a right (resp. left)
 $A$
-module;
$A$
-module;(b)
 $(H_{i}/H_{i+1})J(A/H_{i+1})(H_{i}/H_{i+1})=0$
.
$(H_{i}/H_{i+1})J(A/H_{i+1})(H_{i}/H_{i+1})=0$
.
(2) We call (3.3) a strongly heredity chain if the following conditions hold for any
 $0\leqslant i\leqslant n-1$
:
$0\leqslant i\leqslant n-1$
:(a)
 $H_{i}$
is projective as a right
$H_{i}$
is projective as a right
 $A$
-module and as a left
$A$
-module and as a left
 $A$
-module;
$A$
-module;(b)
 $(H_{i}/H_{i+1})J(A/H_{i+1})(H_{i}/H_{i+1})=0$
.
$(H_{i}/H_{i+1})J(A/H_{i+1})(H_{i}/H_{i+1})=0$
.
Proposition 3.2. Any right-strongly (resp. left-strongly) heredity chain of
![]() $A$
is a heredity chain.
$A$
is a heredity chain.
Proof. Let (3.3) be a right-strongly heredity chain. It is enough to show that
![]() $H_{i}/H_{i+1}$
is projective as a right
$H_{i}/H_{i+1}$
is projective as a right
![]() $(A/H_{i+1})$
-module for any
$(A/H_{i+1})$
-module for any
![]() $0\leqslant i\leqslant n-1$
. Since (3.3) is a right-strongly heredity chain, we have that
$0\leqslant i\leqslant n-1$
. Since (3.3) is a right-strongly heredity chain, we have that
![]() $H_{i}$
is projective as a right
$H_{i}$
is projective as a right
![]() $A$
-module for any
$A$
-module for any
![]() $0\leqslant i\leqslant n-1$
. Hence
$0\leqslant i\leqslant n-1$
. Hence
![]() $H_{i}\otimes _{A}(A/H_{i+1})=H_{i}/H_{i+1}$
is projective as a right
$H_{i}\otimes _{A}(A/H_{i+1})=H_{i}/H_{i+1}$
is projective as a right
![]() $(A/H_{i+1})$
-module for any
$(A/H_{i+1})$
-module for any
![]() $0\leqslant i\leqslant n-1$
.◻
$0\leqslant i\leqslant n-1$
.◻
Example 3.3. Let
![]() $A$
be an artin algebra. Then
$A$
be an artin algebra. Then
![]() $A$
is hereditary if and only if any chain of idempotent ideals of
$A$
is hereditary if and only if any chain of idempotent ideals of
![]() $A$
is a strongly heredity chain.
$A$
is a strongly heredity chain.
Proof. The “only if” part is clear. By [Reference Dlab and Ringel9, Theorem 1],
![]() $A$
is hereditary if and only if any chain of idempotent ideals of
$A$
is hereditary if and only if any chain of idempotent ideals of
![]() $A$
is a heredity chain. Therefore the “if” part follows.◻
$A$
is a heredity chain. Therefore the “if” part follows.◻
Example 3.4. Any heredity chain of length at most two is clearly a right-strongly (resp. left-strongly) heredity chain.
Example 3.5. Let
![]() $A$
be the Auslander algebra of the truncated polynomial algebra
$A$
be the Auslander algebra of the truncated polynomial algebra
![]() $\mathbf{k}[x]/(x^{n})$
. Then
$\mathbf{k}[x]/(x^{n})$
. Then
![]() $A$
is given by the quiver
$A$
is given by the quiver
with relations
![]() $\unicode[STIX]{x1D6FD}_{i}\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{i+1}\unicode[STIX]{x1D6FD}_{i+1}$
(
$\unicode[STIX]{x1D6FD}_{i}\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{i+1}\unicode[STIX]{x1D6FD}_{i+1}$
(
![]() $1\leqslant i\leqslant n-2$
),
$1\leqslant i\leqslant n-2$
),
![]() $\unicode[STIX]{x1D6FD}_{n-1}\unicode[STIX]{x1D6FC}_{n-1}$
. Then
$\unicode[STIX]{x1D6FD}_{n-1}\unicode[STIX]{x1D6FC}_{n-1}$
. Then
is a strongly heredity chain of
![]() $A$
. This example can be explained by Theorem 4.6.
$A$
. This example can be explained by Theorem 4.6.
We prepare the following easy observation.
Lemma 3.6. Let
![]() $A$
be an artin algebra and
$A$
be an artin algebra and
a chain of two-sided ideals. Then the following conditions are equivalent:
(i)
 $H_{i}$
is projective as a right (resp. left)
$H_{i}$
is projective as a right (resp. left)
 $A$
-module for
$A$
-module for
 $0\leqslant i\leqslant n-1$
.
$0\leqslant i\leqslant n-1$
.(ii) The projective dimension of
 $H_{i}/H_{i+1}$
as a right (resp. left)
$H_{i}/H_{i+1}$
as a right (resp. left)
 $A$
-module is at most one for
$A$
-module is at most one for
 $0\leqslant i\leqslant n-1$
.
$0\leqslant i\leqslant n-1$
.
Proof. (i)
![]() $\Rightarrow$
(ii): This is clear from the short exact sequence
$\Rightarrow$
(ii): This is clear from the short exact sequence
![]() $0\rightarrow H_{i+1}\rightarrow H_{i}\rightarrow H_{i}/H_{i+1}\rightarrow 0$
.
$0\rightarrow H_{i+1}\rightarrow H_{i}\rightarrow H_{i}/H_{i+1}\rightarrow 0$
.
(ii)
![]() $\Rightarrow$
(i): Since
$\Rightarrow$
(i): Since
![]() $0\rightarrow H_{1}\rightarrow H_{0}\rightarrow H_{0}/H_{1}\rightarrow 0$
is a short exact sequence such that
$0\rightarrow H_{1}\rightarrow H_{0}\rightarrow H_{0}/H_{1}\rightarrow 0$
is a short exact sequence such that
![]() $H_{0}=A$
is a projective
$H_{0}=A$
is a projective
![]() $A$
-module,
$A$
-module,
![]() $H_{1}$
is also projective as a right
$H_{1}$
is also projective as a right
![]() $A$
-module. Thus we obtain the assertion inductively.◻
$A$
-module. Thus we obtain the assertion inductively.◻
Now, we are ready to prove the following main observation in this subsection.
Proposition 3.7. Let
![]() $A$
be an artin algebra,
$A$
be an artin algebra,
![]() ${\leqslant}$
a total order on
${\leqslant}$
a total order on
![]() $I$
and
$I$
and
a maximal chain of idempotent ideals corresponding to
![]() ${\leqslant}$
by (2.2). Then
${\leqslant}$
by (2.2). Then
![]() $(A,\leqslant )$
is a right-strongly (resp. left-strongly) quasi-hereditary algebra if and only if (3.4) is a right-strongly (resp. left-strongly) heredity chain.
$(A,\leqslant )$
is a right-strongly (resp. left-strongly) quasi-hereditary algebra if and only if (3.4) is a right-strongly (resp. left-strongly) heredity chain.
Proof. Both conditions imply that (3.4) is a heredity chain by Proposition 2.4(1) and Proposition 3.2. Moreover we have an isomorphism
as right
![]() $A$
-modules for some positive integer
$A$
-modules for some positive integer
![]() $m_{j}$
by Proposition 2.4(2).
$m_{j}$
by Proposition 2.4(2).
By (3.5), the pair
![]() $(A,\leqslant )$
is right-strongly quasi-hereditary if and only if the projective dimension of
$(A,\leqslant )$
is right-strongly quasi-hereditary if and only if the projective dimension of
![]() $H_{j}/H_{j+1}$
as a right
$H_{j}/H_{j+1}$
as a right
![]() $A$
-module is at most one for any
$A$
-module is at most one for any
![]() $0\leqslant j\leqslant n-1$
. By Lemma 3.6, this is equivalent to that
$0\leqslant j\leqslant n-1$
. By Lemma 3.6, this is equivalent to that
![]() $H_{j}$
is projective as a right
$H_{j}$
is projective as a right
![]() $A$
-module for any
$A$
-module for any
![]() $0\leqslant j\leqslant n-1$
. Hence (3.4) is a right-strongly heredity chain.◻
$0\leqslant j\leqslant n-1$
. Hence (3.4) is a right-strongly heredity chain.◻
Throughout this paper, we frequently use the following basic observations.
Lemma 3.8. Let
![]() $A$
be an artin algebra and
$A$
be an artin algebra and
![]() $e$
an idempotent of
$e$
an idempotent of
![]() $A$
. Then we have the following statements.
$A$
. Then we have the following statements.
(1) If
 $AeA$
is projective as a right
$AeA$
is projective as a right
 $A$
-module, then
$A$
-module, then
 $AeA\in \mathsf{add}eA$
.
$AeA\in \mathsf{add}eA$
.(2) If
 $Ae$
is projective as a right
$Ae$
is projective as a right
 $(eAe)$
-module, then the functor
$(eAe)$
-module, then the functor
 $\operatorname{Hom}_{A}(eA,-):\mathsf{mod}A\rightarrow \mathsf{mod}eAe$
preserves projective modules. In particular,
$\operatorname{Hom}_{A}(eA,-):\mathsf{mod}A\rightarrow \mathsf{mod}eAe$
preserves projective modules. In particular,
 $\operatorname{gldim}eAe\leqslant \operatorname{gldim}A$
.
$\operatorname{gldim}eAe\leqslant \operatorname{gldim}A$
.(3) If
 $AeA$
is projective as a right
$AeA$
is projective as a right
 $A$
-module, then
$A$
-module, then
 $Ae$
is a projective right
$Ae$
is a projective right
 $(eAe)$
-module.
$(eAe)$
-module.
Proof. (1) Take an epimorphism
![]() $f:(eAe)^{l}{\twoheadrightarrow}Ae$
in
$f:(eAe)^{l}{\twoheadrightarrow}Ae$
in
![]() $\mathsf{mod}(eAe)$
. Composing
$\mathsf{mod}(eAe)$
. Composing
![]() $f\otimes _{eAe}eA:(eA)^{l}{\twoheadrightarrow}Ae\otimes _{eAe}eA$
with the multiplication map
$f\otimes _{eAe}eA:(eA)^{l}{\twoheadrightarrow}Ae\otimes _{eAe}eA$
with the multiplication map
![]() $Ae\otimes _{eAe}eA{\twoheadrightarrow}AeA$
, we have an epimorphism
$Ae\otimes _{eAe}eA{\twoheadrightarrow}AeA$
, we have an epimorphism
![]() $(eA)^{l}{\twoheadrightarrow}AeA$
of right
$(eA)^{l}{\twoheadrightarrow}AeA$
of right
![]() $A$
-modules.
$A$
-modules.
(2) For any
![]() $P\in \mathsf{proj}A$
, we have that
$P\in \mathsf{proj}A$
, we have that
![]() $\operatorname{Hom}_{A}(eA,P)=Pe$
is a direct summand of a finite direct sum of copies of
$\operatorname{Hom}_{A}(eA,P)=Pe$
is a direct summand of a finite direct sum of copies of
![]() $\operatorname{Hom}_{A}(eA,A)=Ae$
. Hence the assertion holds.
$\operatorname{Hom}_{A}(eA,A)=Ae$
. Hence the assertion holds.
(3) Since
![]() $AeA$
is a projective
$AeA$
is a projective
![]() $A$
-module, it follows from (1) that
$A$
-module, it follows from (1) that
![]() $AeA\in \mathsf{add}eA$
. Hence we obtain that
$AeA\in \mathsf{add}eA$
. Hence we obtain that
![]() $Ae=AeAe=\operatorname{Hom}_{A}(eA,AeA)$
is projective as a right
$Ae=AeAe=\operatorname{Hom}_{A}(eA,AeA)$
is projective as a right
![]() $(eAe)$
-module.◻
$(eAe)$
-module.◻
We end this subsection with the following observations which show that right-strongly (resp. left-strongly) quasi-hereditary algebras are closed under idempotent reductions.
Proposition 3.9. Let
![]() $A$
be an artin algebra with a right-strongly (resp. left-strongly) heredity chain
$A$
be an artin algebra with a right-strongly (resp. left-strongly) heredity chain
Then the following statements hold.
(1) For
 $0<i\leqslant n-1$
,
$0<i\leqslant n-1$
,
 $A/H_{i}$
has a right-strongly (resp. left-strongly) heredity chain
$A/H_{i}$
has a right-strongly (resp. left-strongly) heredity chain  $$\begin{eqnarray}A/H_{i}=H_{0}/H_{i}>H_{1}/H_{i}>\cdots >H_{i}/H_{i}=0.\end{eqnarray}$$
$$\begin{eqnarray}A/H_{i}=H_{0}/H_{i}>H_{1}/H_{i}>\cdots >H_{i}/H_{i}=0.\end{eqnarray}$$
(2) Let
 $e_{i}\in A$
be an idempotent of
$e_{i}\in A$
be an idempotent of
 $A$
such that
$A$
such that
 $H_{i}=Ae_{i}A$
for
$H_{i}=Ae_{i}A$
for
 $0\leqslant i\leqslant n-1$
. Then
$0\leqslant i\leqslant n-1$
. Then
 $e_{i}Ae_{i}$
has a right-strongly (resp. left-strongly) heredity chain
$e_{i}Ae_{i}$
has a right-strongly (resp. left-strongly) heredity chain  $$\begin{eqnarray}e_{i}Ae_{i}=e_{i}H_{i}e_{i}>e_{i}H_{i+1}e_{i}>\cdots >e_{i}H_{n}e_{i}=0.\end{eqnarray}$$
$$\begin{eqnarray}e_{i}Ae_{i}=e_{i}H_{i}e_{i}>e_{i}H_{i+1}e_{i}>\cdots >e_{i}H_{n}e_{i}=0.\end{eqnarray}$$
Proof. (1) It is enough to show that
![]() $H_{j}/H_{i}$
is projective as a right
$H_{j}/H_{i}$
is projective as a right
![]() $(A/H_{i})$
-module for
$(A/H_{i})$
-module for
![]() $1\leqslant j<i$
. This is immediate since
$1\leqslant j<i$
. This is immediate since
![]() $H_{j}$
is projective as a right
$H_{j}$
is projective as a right
![]() $A$
-module and the functor
$A$
-module and the functor
![]() $-\otimes _{A}(A/H_{i}):\mathsf{mod}A\rightarrow \mathsf{mod}A/H_{i}$
reflect projectivity.
$-\otimes _{A}(A/H_{i}):\mathsf{mod}A\rightarrow \mathsf{mod}A/H_{i}$
reflect projectivity.
(2) We prove that
![]() $e_{i}H_{j}e_{i}$
is a projective right
$e_{i}H_{j}e_{i}$
is a projective right
![]() $(e_{i}Ae_{i})$
-module. By Lemma 3.8(3), we have that
$(e_{i}Ae_{i})$
-module. By Lemma 3.8(3), we have that
![]() $Ae_{i}$
is projective as a right
$Ae_{i}$
is projective as a right
![]() $(e_{i}Ae_{i})$
-module. It follows from Lemma 3.8(2) that
$(e_{i}Ae_{i})$
-module. It follows from Lemma 3.8(2) that
![]() $H_{j}e_{i}$
is projective as a right
$H_{j}e_{i}$
is projective as a right
![]() $(e_{i}Ae_{i})$
-module. Since
$(e_{i}Ae_{i})$
-module. Since
![]() $H_{j}e_{i}=e_{i}H_{j}e_{i}\oplus (1-e_{i})H_{j}e_{i}$
, we have
$H_{j}e_{i}=e_{i}H_{j}e_{i}\oplus (1-e_{i})H_{j}e_{i}$
, we have
![]() $e_{i}H_{j}e_{i}\in \mathsf{proj}(e_{i}Ae_{i})$
.◻
$e_{i}H_{j}e_{i}\in \mathsf{proj}(e_{i}Ae_{i})$
.◻
3.2 Right rejective subcategories
In this subsection, we recall the definitions of right rejective subcategories. Using them, we characterize right-strongly (resp. left-strongly) quasi-hereditary algebras. We refer to [Reference Assem, Simson and Skowroński1, Appendix] for background on category theory.
Let
![]() ${\mathcal{C}}$
be an additive category, and put
${\mathcal{C}}$
be an additive category, and put
![]() ${\mathcal{C}}(X,Y):=\operatorname{Hom}_{{\mathcal{C}}}(X,Y)$
. In the rest of this paper, we assume that any subcategory is full and closed under isomorphisms, direct sums and direct summands. We denote by
${\mathcal{C}}(X,Y):=\operatorname{Hom}_{{\mathcal{C}}}(X,Y)$
. In the rest of this paper, we assume that any subcategory is full and closed under isomorphisms, direct sums and direct summands. We denote by
![]() ${\mathcal{J}}_{{\mathcal{C}}}$
the Jacobson radical of
${\mathcal{J}}_{{\mathcal{C}}}$
the Jacobson radical of
![]() ${\mathcal{C}}$
, and by
${\mathcal{C}}$
, and by
![]() $\mathsf{ind}{\mathcal{C}}$
the set of isoclasses of indecomposable objects in
$\mathsf{ind}{\mathcal{C}}$
the set of isoclasses of indecomposable objects in
![]() ${\mathcal{C}}$
. For a subcategory
${\mathcal{C}}$
. For a subcategory
![]() ${\mathcal{C}}^{\prime }$
of
${\mathcal{C}}^{\prime }$
of
![]() ${\mathcal{C}}$
, we denote by
${\mathcal{C}}$
, we denote by
![]() $[{\mathcal{C}}^{\prime }]$
the ideal of
$[{\mathcal{C}}^{\prime }]$
the ideal of
![]() ${\mathcal{C}}$
consisting of morphisms which factor through some object of
${\mathcal{C}}$
consisting of morphisms which factor through some object of
![]() ${\mathcal{C}}^{\prime }$
. For an ideal
${\mathcal{C}}^{\prime }$
. For an ideal
![]() ${\mathcal{I}}$
of
${\mathcal{I}}$
of
![]() ${\mathcal{C}}$
, the factor category
${\mathcal{C}}$
, the factor category
![]() ${\mathcal{C}}/{\mathcal{I}}$
is defined by
${\mathcal{C}}/{\mathcal{I}}$
is defined by
![]() $\mathit{ob}({\mathcal{C}}/{\mathcal{I}}):=\mathit{ob}({\mathcal{C}})$
and
$\mathit{ob}({\mathcal{C}}/{\mathcal{I}}):=\mathit{ob}({\mathcal{C}})$
and
![]() $({\mathcal{C}}/{\mathcal{I}})(X,Y):={\mathcal{C}}(X,Y)/{\mathcal{I}}(X,Y)$
for any
$({\mathcal{C}}/{\mathcal{I}})(X,Y):={\mathcal{C}}(X,Y)/{\mathcal{I}}(X,Y)$
for any
![]() $X,Y\in {\mathcal{C}}$
. Recall that an additive category
$X,Y\in {\mathcal{C}}$
. Recall that an additive category
![]() ${\mathcal{C}}$
is called Krull–Schmidt if any object of
${\mathcal{C}}$
is called Krull–Schmidt if any object of
![]() ${\mathcal{C}}$
is isomorphic to finite direct sum of objects whose endomorphism rings are local.
${\mathcal{C}}$
is isomorphic to finite direct sum of objects whose endomorphism rings are local.
Definition 3.10. (Auslander–Smalø [Reference Auslander and Smalø4])
Let
![]() ${\mathcal{C}}$
be an additive category and
${\mathcal{C}}$
be an additive category and
![]() ${\mathcal{C}}^{\prime }$
a subcategory of
${\mathcal{C}}^{\prime }$
a subcategory of
![]() ${\mathcal{C}}$
. We say that
${\mathcal{C}}$
. We say that
![]() $f\in {\mathcal{C}}(Y,X)$
is a right
$f\in {\mathcal{C}}(Y,X)$
is a right
![]() ${\mathcal{C}}^{\prime }$
-approximation of
${\mathcal{C}}^{\prime }$
-approximation of
![]() $X$
if the following equivalent conditions are satisfied.
$X$
if the following equivalent conditions are satisfied.
(i)
 $Y\in {\mathcal{C}}^{\prime }$
and
$Y\in {\mathcal{C}}^{\prime }$
and
 ${\mathcal{C}}(-,Y)\xrightarrow[{}]{f\circ -}{\mathcal{C}}(-,X)\rightarrow 0$
is exact on
${\mathcal{C}}(-,Y)\xrightarrow[{}]{f\circ -}{\mathcal{C}}(-,X)\rightarrow 0$
is exact on
 ${\mathcal{C}}^{\prime }$
.
${\mathcal{C}}^{\prime }$
.(ii)
 $Y\in {\mathcal{C}}^{\prime }$
and the induced morphism
$Y\in {\mathcal{C}}^{\prime }$
and the induced morphism
 ${\mathcal{C}}(-,Y)\xrightarrow[{}]{f\circ -}[{\mathcal{C}}^{\prime }](-,X)$
is an epimorphism on
${\mathcal{C}}(-,Y)\xrightarrow[{}]{f\circ -}[{\mathcal{C}}^{\prime }](-,X)$
is an epimorphism on
 ${\mathcal{C}}$
.
${\mathcal{C}}$
.Dually, a left
 ${\mathcal{C}}^{^{\prime }}$
-approximation is defined.
${\mathcal{C}}^{^{\prime }}$
-approximation is defined.
Now, we introduce the following key notions in this paper.
Definition 3.11. (Iyama [Reference Iyama16, 2.1(1)])
Let
![]() ${\mathcal{C}}$
be an additive category and
${\mathcal{C}}$
be an additive category and
![]() ${\mathcal{C}}^{\prime }$
a subcategory of
${\mathcal{C}}^{\prime }$
a subcategory of
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
(1) We call
 ${\mathcal{C}}^{\prime }$
a right (resp. left) rejective subcategory of
${\mathcal{C}}^{\prime }$
a right (resp. left) rejective subcategory of
 ${\mathcal{C}}$
if the inclusion functor
${\mathcal{C}}$
if the inclusion functor
 ${\mathcal{C}}^{\prime }{\hookrightarrow}{\mathcal{C}}$
has a right (resp. left) adjoint with a counit
${\mathcal{C}}^{\prime }{\hookrightarrow}{\mathcal{C}}$
has a right (resp. left) adjoint with a counit
 $\unicode[STIX]{x1D700}^{-}$
(resp. unit
$\unicode[STIX]{x1D700}^{-}$
(resp. unit
 $\unicode[STIX]{x1D700}^{+}$
) such that
$\unicode[STIX]{x1D700}^{+}$
) such that
 $\unicode[STIX]{x1D700}_{X}^{-}$
is a monomorphism (resp.
$\unicode[STIX]{x1D700}_{X}^{-}$
is a monomorphism (resp.
 $\unicode[STIX]{x1D700}_{X}^{+}$
is an epimorphism) for
$\unicode[STIX]{x1D700}_{X}^{+}$
is an epimorphism) for
 $X\in {\mathcal{C}}$
.
$X\in {\mathcal{C}}$
.(2) We call
 ${\mathcal{C}}^{\prime }$
a rejective subcategory of
${\mathcal{C}}^{\prime }$
a rejective subcategory of
 ${\mathcal{C}}$
if
${\mathcal{C}}$
if
 ${\mathcal{C}}^{\prime }$
is a right and left rejective subcategory of
${\mathcal{C}}^{\prime }$
is a right and left rejective subcategory of
 ${\mathcal{C}}$
.
${\mathcal{C}}$
.
We often use the following equivalent conditions.
Proposition 3.12. (Iyama [Reference Iyama17, Definition 1.5])
Let
![]() ${\mathcal{C}}$
be an additive category and
${\mathcal{C}}$
be an additive category and
![]() ${\mathcal{C}}^{\prime }$
a subcategory of
${\mathcal{C}}^{\prime }$
a subcategory of
![]() ${\mathcal{C}}$
. Then the following are equivalent:
${\mathcal{C}}$
. Then the following are equivalent:
(i)
 ${\mathcal{C}}^{\prime }$
is a right (resp. left) rejective subcategory of
${\mathcal{C}}^{\prime }$
is a right (resp. left) rejective subcategory of
 ${\mathcal{C}}$
.
${\mathcal{C}}$
.(ii) For any
 $X\in {\mathcal{C}}$
, there exists a monic right (resp. epic left)
$X\in {\mathcal{C}}$
, there exists a monic right (resp. epic left)
 ${\mathcal{C}}^{\prime }$
-approximation
${\mathcal{C}}^{\prime }$
-approximation
 $f_{X}\in {\mathcal{C}}(Y,X)$
(resp.
$f_{X}\in {\mathcal{C}}(Y,X)$
(resp.
 $f^{X}\in {\mathcal{C}}(X,Y)$
) of
$f^{X}\in {\mathcal{C}}(X,Y)$
) of
 $X$
.
$X$
.
Proof. (i)
![]() $\Rightarrow$
(ii): If the inclusion functor
$\Rightarrow$
(ii): If the inclusion functor
![]() $F:{\mathcal{C}}^{\prime }{\hookrightarrow}{\mathcal{C}}$
has a right adjoint
$F:{\mathcal{C}}^{\prime }{\hookrightarrow}{\mathcal{C}}$
has a right adjoint
![]() $G$
with a counit
$G$
with a counit
![]() $\unicode[STIX]{x1D700}^{-}$
, then
$\unicode[STIX]{x1D700}^{-}$
, then
![]() $\unicode[STIX]{x1D700}_{X}^{-}:G(X)\rightarrow X$
is a right
$\unicode[STIX]{x1D700}_{X}^{-}:G(X)\rightarrow X$
is a right
![]() ${\mathcal{C}}^{\prime }$
-approximation of
${\mathcal{C}}^{\prime }$
-approximation of
![]() $X\in {\mathcal{C}}$
. Thus the assertion follows.
$X\in {\mathcal{C}}$
. Thus the assertion follows.
(ii)
![]() $\Rightarrow$
(i): We assume that, for any
$\Rightarrow$
(i): We assume that, for any
![]() $X\in {\mathcal{C}}$
, there exists a monic right
$X\in {\mathcal{C}}$
, there exists a monic right
![]() ${\mathcal{C}}^{\prime }$
-approximation of
${\mathcal{C}}^{\prime }$
-approximation of
![]() $X$
. We construct a right adjoint functor
$X$
. We construct a right adjoint functor
![]() $G:{\mathcal{C}}\rightarrow {\mathcal{C}}^{\prime }$
as follows. For
$G:{\mathcal{C}}\rightarrow {\mathcal{C}}^{\prime }$
as follows. For
![]() $X\in {\mathcal{C}}$
, take a monic right
$X\in {\mathcal{C}}$
, take a monic right
![]() ${\mathcal{C}}^{\prime }$
-approximation
${\mathcal{C}}^{\prime }$
-approximation
![]() $f_{X}:C_{X}\rightarrow X$
. For a morphism
$f_{X}:C_{X}\rightarrow X$
. For a morphism
![]() $\unicode[STIX]{x1D711}\in {\mathcal{C}}(X,Y)$
, there exists a unique morphism
$\unicode[STIX]{x1D711}\in {\mathcal{C}}(X,Y)$
, there exists a unique morphism
![]() $C_{\unicode[STIX]{x1D711}}:C_{X}\rightarrow C_{Y}$
making the following diagram commutative.
$C_{\unicode[STIX]{x1D711}}:C_{X}\rightarrow C_{Y}$
making the following diagram commutative.

It is easy to check that
![]() $G(X):=C_{X}$
and
$G(X):=C_{X}$
and
![]() $G(\unicode[STIX]{x1D711}):=C_{\unicode[STIX]{x1D711}}$
give a right adjoint functor
$G(\unicode[STIX]{x1D711}):=C_{\unicode[STIX]{x1D711}}$
give a right adjoint functor
![]() $G:{\mathcal{C}}\rightarrow {\mathcal{C}}^{\prime }$
of the inclusion functor
$G:{\mathcal{C}}\rightarrow {\mathcal{C}}^{\prime }$
of the inclusion functor
![]() $F:{\mathcal{C}}^{\prime }\rightarrow {\mathcal{C}}$
and
$F:{\mathcal{C}}^{\prime }\rightarrow {\mathcal{C}}$
and
![]() $f$
gives a counit.◻
$f$
gives a counit.◻
Right rejective subcategories of
![]() $\mathsf{mod}A$
are characterized as follows.
$\mathsf{mod}A$
are characterized as follows.
Proposition 3.13. (Iyama [Reference Iyama17, Proposition 1.5.2])
Let
![]() $A$
be an artin algebra and
$A$
be an artin algebra and
![]() ${\mathcal{C}}$
a subcategory of
${\mathcal{C}}$
a subcategory of
![]() $\mathsf{mod}A$
. Then
$\mathsf{mod}A$
. Then
![]() ${\mathcal{C}}$
is a right (resp. left) rejective subcategory of
${\mathcal{C}}$
is a right (resp. left) rejective subcategory of
![]() $\mathsf{mod}A$
if and only if
$\mathsf{mod}A$
if and only if
![]() ${\mathcal{C}}$
is closed under factor modules (resp. submodules).
${\mathcal{C}}$
is closed under factor modules (resp. submodules).
Proof. We show the “if” part. For
![]() $M\in \mathsf{mod}A$
, we put
$M\in \mathsf{mod}A$
, we put
![]() $G(M):=\sum _{X\in {\mathcal{C}},f\in \operatorname{Hom}_{A}(X,M)}f(X)$
. Then
$G(M):=\sum _{X\in {\mathcal{C}},f\in \operatorname{Hom}_{A}(X,M)}f(X)$
. Then
![]() $G(M)$
is a factor module of some module in
$G(M)$
is a factor module of some module in
![]() ${\mathcal{C}}$
. Thus we have
${\mathcal{C}}$
. Thus we have
![]() $G(M)\in {\mathcal{C}}$
. Since the natural inclusion
$G(M)\in {\mathcal{C}}$
. Since the natural inclusion
![]() $G(M){\hookrightarrow}M$
is a monic right
$G(M){\hookrightarrow}M$
is a monic right
![]() ${\mathcal{C}}$
-approximation of
${\mathcal{C}}$
-approximation of
![]() $M$
, the assertion holds.
$M$
, the assertion holds.
We show the “only if” part. For a surjection
![]() $f:M\rightarrow N$
with
$f:M\rightarrow N$
with
![]() $M\in {\mathcal{C}}$
, we show that
$M\in {\mathcal{C}}$
, we show that
![]() $N$
belongs to
$N$
belongs to
![]() ${\mathcal{C}}$
. Since
${\mathcal{C}}$
. Since
![]() ${\mathcal{C}}$
is a right rejective subcategory of
${\mathcal{C}}$
is a right rejective subcategory of
![]() $\mathsf{mod}A$
, there exists a monic right
$\mathsf{mod}A$
, there exists a monic right
![]() ${\mathcal{C}}$
-approximation
${\mathcal{C}}$
-approximation
![]() $f_{N}:G(N)\rightarrow N$
of
$f_{N}:G(N)\rightarrow N$
of
![]() $N$
. Thus we have a morphism
$N$
. Thus we have a morphism
![]() $g:M\rightarrow G(N)$
such that
$g:M\rightarrow G(N)$
such that
![]() $f=f_{N}\circ g$
. Since
$f=f_{N}\circ g$
. Since
![]() $f$
is surjective, we have that
$f$
is surjective, we have that
![]() $f_{N}$
is a bijection. Hence we have
$f_{N}$
is a bijection. Hence we have
![]() $N\in {\mathcal{C}}$
.◻
$N\in {\mathcal{C}}$
.◻
Proposition 3.14. (Iyama [Reference Iyama17, Theorem 1.6.1(1)])
Let
![]() $A$
be an artin algebra. Then there exists a bijection between factor algebras
$A$
be an artin algebra. Then there exists a bijection between factor algebras
![]() $B$
of
$B$
of
![]() $A$
and rejective subcategories
$A$
and rejective subcategories
![]() ${\mathcal{C}}$
of
${\mathcal{C}}$
of
![]() $\mathsf{mod}A$
given by
$\mathsf{mod}A$
given by
![]() $B\mapsto \mathsf{mod}B$
.
$B\mapsto \mathsf{mod}B$
.
Proof. This is clearly from Proposition 3.13 since a full subcategory of
![]() $\mathsf{mod}A$
which is closed under submodules and factor modules is precisely
$\mathsf{mod}A$
which is closed under submodules and factor modules is precisely
![]() $\mathsf{mod}B$
for a factor algebra
$\mathsf{mod}B$
for a factor algebra
![]() $B$
of
$B$
of
![]() $A$
.◻
$A$
.◻
Example 3.15. Let
![]() $A$
be an artin algebra.
$A$
be an artin algebra.
(a) Let
 $({\mathcal{T}},{\mathcal{F}})$
be a torsion pair on
$({\mathcal{T}},{\mathcal{F}})$
be a torsion pair on
 $\mathsf{mod}A$
. Then
$\mathsf{mod}A$
. Then
 ${\mathcal{T}}$
is a right rejective subcategory and
${\mathcal{T}}$
is a right rejective subcategory and
 ${\mathcal{F}}$
is a left rejective subcategory of
${\mathcal{F}}$
is a left rejective subcategory of
 $\mathsf{mod}A$
by Proposition 3.13.
$\mathsf{mod}A$
by Proposition 3.13.(b) For a classical tilting
 $A$
-module
$A$
-module
 $T$
, we put
$T$
, we put
 ${\mathcal{T}}:=\{Y\in \mathsf{mod}A\mid \operatorname{Ext}_{A}^{1}(T,Y)=0\}$
and
${\mathcal{T}}:=\{Y\in \mathsf{mod}A\mid \operatorname{Ext}_{A}^{1}(T,Y)=0\}$
and
 ${\mathcal{F}}:=\{Y\in \mathsf{mod}A\mid \operatorname{Hom}_{A}(T,Y)=0\}$
. Then
${\mathcal{F}}:=\{Y\in \mathsf{mod}A\mid \operatorname{Hom}_{A}(T,Y)=0\}$
. Then
 $({\mathcal{T}},{\mathcal{F}})$
is a torsion pair on
$({\mathcal{T}},{\mathcal{F}})$
is a torsion pair on
 $\mathsf{mod}A$
, and therefore
$\mathsf{mod}A$
, and therefore
 ${\mathcal{T}}$
(resp.
${\mathcal{T}}$
(resp.
 ${\mathcal{F}}$
) is a right (resp. left) rejective subcategory of
${\mathcal{F}}$
) is a right (resp. left) rejective subcategory of
 $\mathsf{mod}A$
.
$\mathsf{mod}A$
.(c) Assume that
 $A$
is right-strongly quasi-hereditary and let
$A$
is right-strongly quasi-hereditary and let
 $T$
be a characteristic tilting module. Then
$T$
be a characteristic tilting module. Then
 $T$
is a classical tilting module [Reference Dlab and Ringel10, Lemma 4.1] and hence
$T$
is a classical tilting module [Reference Dlab and Ringel10, Lemma 4.1] and hence
 $({\mathcal{T}},{\mathcal{F}})$
is a torsion pair on
$({\mathcal{T}},{\mathcal{F}})$
is a torsion pair on
 $\mathsf{mod}A$
. Since
$\mathsf{mod}A$
. Since
 ${\mathcal{T}}$
coincides with the subcategory
${\mathcal{T}}$
coincides with the subcategory
 ${\mathcal{F}}(\unicode[STIX]{x1D6E5})^{\bot }:=\{Y\in \mathsf{mod}A\mid \operatorname{Ext}_{A}^{i}({\mathcal{F}}(\unicode[STIX]{x1D6E5}),Y)=0\text{ for all }i\geqslant 1\}$
[Reference Dlab and Ringel10, Section 4], we have that
${\mathcal{F}}(\unicode[STIX]{x1D6E5})^{\bot }:=\{Y\in \mathsf{mod}A\mid \operatorname{Ext}_{A}^{i}({\mathcal{F}}(\unicode[STIX]{x1D6E5}),Y)=0\text{ for all }i\geqslant 1\}$
[Reference Dlab and Ringel10, Section 4], we have that
 ${\mathcal{F}}(\unicode[STIX]{x1D6E5})^{\bot }$
is a right rejective subcategory of
${\mathcal{F}}(\unicode[STIX]{x1D6E5})^{\bot }$
is a right rejective subcategory of
 $\mathsf{mod}A$
.
$\mathsf{mod}A$
.
Right rejective subcategories of
![]() $\mathsf{proj}A$
are characterized as follows.
$\mathsf{proj}A$
are characterized as follows.
Proposition 3.16. (Iyama [Reference Iyama17, Theorem 3.2 (2)])
Let
![]() $A$
be an artin algebra and
$A$
be an artin algebra and
![]() $e$
an idempotent of
$e$
an idempotent of
![]() $A$
. Then
$A$
. Then
![]() $\mathsf{add}eA$
is a right (resp. left) rejective subcategory of
$\mathsf{add}eA$
is a right (resp. left) rejective subcategory of
![]() $\mathsf{proj}A$
if and only if
$\mathsf{proj}A$
if and only if
![]() $AeA$
is a projective right (resp. left)
$AeA$
is a projective right (resp. left)
![]() $A$
-module. In this case, we have
$A$
-module. In this case, we have
![]() $\operatorname{gldim}eAe\leqslant \operatorname{gldim}A$
.
$\operatorname{gldim}eAe\leqslant \operatorname{gldim}A$
.
Proof. Assume that
![]() $\mathsf{add}eA$
is a right rejective subcategory of
$\mathsf{add}eA$
is a right rejective subcategory of
![]() $\mathsf{proj}A$
. Then there exists
$\mathsf{proj}A$
. Then there exists
![]() $a\in \operatorname{Hom}_{A}(P,A)$
with
$a\in \operatorname{Hom}_{A}(P,A)$
with
![]() $P\in \mathsf{add}(eA)_{A}$
such that
$P\in \mathsf{add}(eA)_{A}$
such that
is an isomorphism. Hence
![]() $AeA\cong P$
is a projective right
$AeA\cong P$
is a projective right
![]() $A$
-module.
$A$
-module.
Conversely, we assume that
![]() $AeA$
is a projective right
$AeA$
is a projective right
![]() $A$
-module. By Lemma 3.8(1), we have
$A$
-module. By Lemma 3.8(1), we have
![]() $AeA\in \mathsf{add}eA$
as a right
$AeA\in \mathsf{add}eA$
as a right
![]() $A$
-module. The inclusion map
$A$
-module. The inclusion map
![]() $i:AeA{\hookrightarrow}A$
gives a right
$i:AeA{\hookrightarrow}A$
gives a right
![]() $(\mathsf{add}eA)$
-approximation of
$(\mathsf{add}eA)$
-approximation of
![]() $A$
since
$A$
since
is an isomorphism.
In this case,
![]() $Ae$
is projective as a right
$Ae$
is projective as a right
![]() $(eAe)$
-module by Lemma 3.8(3). Thus it follows from Lemma 3.8(2) that
$(eAe)$
-module by Lemma 3.8(3). Thus it follows from Lemma 3.8(2) that
![]() $\operatorname{gldim}eAe\leqslant \operatorname{gldim}A$
.
$\operatorname{gldim}eAe\leqslant \operatorname{gldim}A$
.
By the duality
![]() $\operatorname{Hom}_{A}(-,A):\mathsf{proj}A\rightarrow \mathsf{proj}A^{\operatorname{op}}$
, we have that
$\operatorname{Hom}_{A}(-,A):\mathsf{proj}A\rightarrow \mathsf{proj}A^{\operatorname{op}}$
, we have that
![]() $\mathsf{add}eA$
is left rejective in
$\mathsf{add}eA$
is left rejective in
![]() $\mathsf{proj}A$
if and only if
$\mathsf{proj}A$
if and only if
![]() $\mathsf{add}Ae$
is right rejective in
$\mathsf{add}Ae$
is right rejective in
![]() $\mathsf{proj}A^{\operatorname{op}}$
. Hence the statement for left rejective subcategories follows.◻
$\mathsf{proj}A^{\operatorname{op}}$
. Hence the statement for left rejective subcategories follows.◻
To introduce rejective chains, we need the following notion.
Definition 3.17. Let
![]() ${\mathcal{C}}$
be a Krull–Schmidt category.
${\mathcal{C}}$
be a Krull–Schmidt category.
(1) We call
 ${\mathcal{C}}$
a semisimple category if
${\mathcal{C}}$
a semisimple category if
 ${\mathcal{J}}_{{\mathcal{C}}}=0$
.
${\mathcal{J}}_{{\mathcal{C}}}=0$
.(2) A subcategory
 ${\mathcal{C}}^{\prime }$
of
${\mathcal{C}}^{\prime }$
of
 ${\mathcal{C}}$
is called cosemisimple in
${\mathcal{C}}$
is called cosemisimple in
 ${\mathcal{C}}$
if the factor category
${\mathcal{C}}$
if the factor category
 ${\mathcal{C}}/[{\mathcal{C}}^{\prime }]$
is semisimple.
${\mathcal{C}}/[{\mathcal{C}}^{\prime }]$
is semisimple.
We often use the fact that
![]() ${\mathcal{C}}^{\prime }$
is a cosemisimple subcategory of
${\mathcal{C}}^{\prime }$
is a cosemisimple subcategory of
![]() ${\mathcal{C}}$
if and only if
${\mathcal{C}}$
if and only if
![]() $[{\mathcal{C}}^{\prime }](-,X)={\mathcal{J}}_{{\mathcal{C}}}(-,X)$
holds for any
$[{\mathcal{C}}^{\prime }](-,X)={\mathcal{J}}_{{\mathcal{C}}}(-,X)$
holds for any
![]() $X\in \mathsf{ind}{\mathcal{C}}\setminus \mathsf{ind}{\mathcal{C}}^{\prime }$
.
$X\in \mathsf{ind}{\mathcal{C}}\setminus \mathsf{ind}{\mathcal{C}}^{\prime }$
.
Lemma 3.18. Let
![]() $A$
be an artin algebra and
$A$
be an artin algebra and
![]() $Ae^{\prime }A\subset AeA$
idempotent ideals of
$Ae^{\prime }A\subset AeA$
idempotent ideals of
![]() $A$
. Then the following conditions are equivalent:
$A$
. Then the following conditions are equivalent:
(i)
 $\mathsf{add}e^{\prime }A$
is a cosemisimple subcategory of
$\mathsf{add}e^{\prime }A$
is a cosemisimple subcategory of
 $\mathsf{add}eA$
.
$\mathsf{add}eA$
.(ii)
 $J(eAe/eAe^{\prime }Ae)=0$
.
$J(eAe/eAe^{\prime }Ae)=0$
.(iii)
 $(AeA/Ae^{\prime }A)J(A/Ae^{\prime }A)(AeA/Ae^{\prime }A)=0$
.
$(AeA/Ae^{\prime }A)J(A/Ae^{\prime }A)(AeA/Ae^{\prime }A)=0$
.
Proof. (i)
![]() $\Leftrightarrow$
(ii): Let
$\Leftrightarrow$
(ii): Let
![]() ${\mathcal{C}}:=\mathsf{add}eA/[\mathsf{add}e^{\prime }A]$
. The condition (i) means
${\mathcal{C}}:=\mathsf{add}eA/[\mathsf{add}e^{\prime }A]$
. The condition (i) means
![]() ${\mathcal{J}}_{{\mathcal{C}}}=0$
. This is equivalent to (ii) since
${\mathcal{J}}_{{\mathcal{C}}}=0$
. This is equivalent to (ii) since
![]() ${\mathcal{J}}_{{\mathcal{C}}}(eA,eA)=J(\operatorname{End}_{{\mathcal{C}}}(eA))=J(eAe/eAe^{\prime }Ae)$
.
${\mathcal{J}}_{{\mathcal{C}}}(eA,eA)=J(\operatorname{End}_{{\mathcal{C}}}(eA))=J(eAe/eAe^{\prime }Ae)$
.
(ii)
![]() $\Leftrightarrow$
(iii): Since
$\Leftrightarrow$
(iii): Since
![]() $J(eAe/eAe^{\prime }Ae)=eJ(A/Ae^{\prime }A)e$
, we have the assertion.◻
$J(eAe/eAe^{\prime }Ae)=eJ(A/Ae^{\prime }A)e$
, we have the assertion.◻
Now, we introduce the following central notion in this paper.
Definition 3.19. (Iyama [Reference Iyama16, 2.1(2)], [Reference Iyama17, Definition 2.2])
Let
![]() ${\mathcal{C}}$
be an additive category and
${\mathcal{C}}$
be an additive category and
a chain of subcategories.
(1) We call (3.6) a rejective chain (resp. right rejective, left rejective) if
 ${\mathcal{C}}_{i}$
is a cosemisimple rejective (resp. right rejective, left rejective) subcategory of
${\mathcal{C}}_{i}$
is a cosemisimple rejective (resp. right rejective, left rejective) subcategory of
 ${\mathcal{C}}_{i-1}$
for
${\mathcal{C}}_{i-1}$
for
 $1\leqslant i\leqslant n$
.
$1\leqslant i\leqslant n$
.(2) We call (3.6) a total right (resp. left) rejective chain if the following conditions hold for
 $1\leqslant i\leqslant n$
:
$1\leqslant i\leqslant n$
:(a)
 ${\mathcal{C}}_{i}$
is a right (resp. left) rejective subcategory of
${\mathcal{C}}_{i}$
is a right (resp. left) rejective subcategory of
 ${\mathcal{C}}$
;
${\mathcal{C}}$
;(b)
 ${\mathcal{C}}_{i}$
is a cosemisimple subcategory of
${\mathcal{C}}_{i}$
is a cosemisimple subcategory of
 ${\mathcal{C}}_{i-1}$
.
${\mathcal{C}}_{i-1}$
.
Remark 3.20.
(1) Rejective chains are total right rejective chains and total left rejective chains [Reference Iyama17, 2.1(3)].
(2) Our total right rejective chains are called right rejective chains in [Reference Iyama18, Definition 2.6].
Example 3.21. Let
![]() $A$
be the
$A$
be the
![]() $\mathbf{k}$
-algebra given in Example 2.7. Then
$\mathbf{k}$
-algebra given in Example 2.7. Then
is a total right rejective chain of
![]() $\mathsf{proj}A$
. In fact, the conditions (a) and (b) in Definition 3.19(2) are satisfied by Proposition 3.16 and
$\mathsf{proj}A$
. In fact, the conditions (a) and (b) in Definition 3.19(2) are satisfied by Proposition 3.16 and
![]() $e_{1}J(A)e_{1}=0=e_{2}J(A)e_{2}$
, respectively.
$e_{1}J(A)e_{1}=0=e_{2}J(A)e_{2}$
, respectively.
Now, we are ready to prove the following main result.
Theorem 3.22. Let
![]() $A$
be an artin algebra and
$A$
be an artin algebra and
a chain of idempotent ideals of
![]() $A$
. For
$A$
. For
![]() $0\leqslant i\leqslant n-1$
, we write
$0\leqslant i\leqslant n-1$
, we write
![]() $H_{i}=Ae_{i}A$
, where
$H_{i}=Ae_{i}A$
, where
![]() $e_{i}$
is an idempotent of
$e_{i}$
is an idempotent of
![]() $A$
. Then the following conditions are equivalent:
$A$
. Then the following conditions are equivalent:
(i) The chain (3.7) is a right-strongly (resp. left-strongly) heredity chain.
(ii) The following chain is a total right (resp. left) rejective chain of
 $\mathsf{proj}A$
.
$\mathsf{proj}A$
.  $$\begin{eqnarray}\mathsf{proj}A=\mathsf{add}e_{0}A\supset \mathsf{add}e_{1}A\supset \cdots \supset \mathsf{add}e_{n}A=0.\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{proj}A=\mathsf{add}e_{0}A\supset \mathsf{add}e_{1}A\supset \cdots \supset \mathsf{add}e_{n}A=0.\end{eqnarray}$$
In particular, an artin algebra
![]() $A$
is strongly (resp. right-strongly, left-strongly) quasi-hereditary if and only if
$A$
is strongly (resp. right-strongly, left-strongly) quasi-hereditary if and only if
![]() $\mathsf{proj}A$
has a rejective (resp. total right rejective, total left rejective) chain.
$\mathsf{proj}A$
has a rejective (resp. total right rejective, total left rejective) chain.
Proof. It follows from Proposition 3.16 that
![]() $H_{i}\in \mathsf{proj}A$
if and only if
$H_{i}\in \mathsf{proj}A$
if and only if
![]() $\mathsf{add}e_{i}A$
is a right rejective subcategory of
$\mathsf{add}e_{i}A$
is a right rejective subcategory of
![]() $\mathsf{proj}A$
. Thus we have that
$\mathsf{proj}A$
. Thus we have that
![]() $H_{i}$
satisfies the condition (a) in Definition 3.1(1) if and only if
$H_{i}$
satisfies the condition (a) in Definition 3.1(1) if and only if
![]() $\mathsf{add}e_{i}A$
satisfies the condition (a) in Definition 3.19(2). From Lemma 3.18, we have that
$\mathsf{add}e_{i}A$
satisfies the condition (a) in Definition 3.19(2). From Lemma 3.18, we have that
![]() $(H_{i}/H_{i+1})J(A/H_{i+1})(H_{i}/H_{i+1})=0$
holds if and only if
$(H_{i}/H_{i+1})J(A/H_{i+1})(H_{i}/H_{i+1})=0$
holds if and only if
![]() $\mathsf{add}e_{i+1}A$
is a cosemisimple subcategory of
$\mathsf{add}e_{i+1}A$
is a cosemisimple subcategory of
![]() $\mathsf{add}e_{i}A$
. Thus we obtain that
$\mathsf{add}e_{i}A$
. Thus we obtain that
![]() $H_{i}$
and
$H_{i}$
and
![]() $H_{i+1}$
satisfy the condition (b) in Definition 3.1(1) if and only if
$H_{i+1}$
satisfy the condition (b) in Definition 3.1(1) if and only if
![]() $\mathsf{add}e_{i}A$
and
$\mathsf{add}e_{i}A$
and
![]() $\mathsf{add}e_{i+1}A$
satisfy the condition (b) in Definition 3.19(2).◻
$\mathsf{add}e_{i+1}A$
satisfy the condition (b) in Definition 3.19(2).◻
We apply Theorem 3.22 to the following well-known result.
Corollary 3.23. Let
![]() $A$
be an artin algebra.
$A$
be an artin algebra.
(1) (Iyama [Reference Iyama16, Theorem 1.1]) For any
 $M\in \mathsf{mod}A$
, there exists
$M\in \mathsf{mod}A$
, there exists
 $N\in \mathsf{mod}A$
such that
$N\in \mathsf{mod}A$
such that
 $\mathsf{add}N$
contains
$\mathsf{add}N$
contains
 $M$
and has a total right rejective chain.
$M$
and has a total right rejective chain.(2) (Ringel [Reference Ringel22, Theorem in Section 5]) There exist a right-strongly quasi-hereditary algebra
 $B$
and an idempotent
$B$
and an idempotent
 $e$
of
$e$
of
 $B$
such that
$B$
such that
 $A=eBe$
.
$A=eBe$
.
Proof. (1) For the reader’s convenience, we recall the construction. Let
![]() $M_{0}:=M$
and
$M_{0}:=M$
and
![]() $M_{i+1}:=J(\text{End}_{A}(M_{i}))M_{i}$
inductively. We take the smallest
$M_{i+1}:=J(\text{End}_{A}(M_{i}))M_{i}$
inductively. We take the smallest
![]() $n>0$
such that
$n>0$
such that
![]() $M_{n}=0$
, and let
$M_{n}=0$
, and let
![]() $N:=\bigoplus _{k=0}^{n-1}M_{k}$
and
$N:=\bigoplus _{k=0}^{n-1}M_{k}$
and
![]() ${\mathcal{C}}_{i}:=\mathsf{add}(\bigoplus _{k=i}^{n-1}M_{k})$
. Then
${\mathcal{C}}_{i}:=\mathsf{add}(\bigoplus _{k=i}^{n-1}M_{k})$
. Then
is a total right rejective chain [Reference Iyama16, Lemma 2,2], [Reference Iyama18, Theorem 3.4.1].
(2) Applying (1) to
![]() $M=A$
, we obtain that
$M=A$
, we obtain that
![]() $N\in \mathsf{mod}A$
such that
$N\in \mathsf{mod}A$
such that
![]() $B=\operatorname{End}_{A}(N)$
is right-strongly quasi-hereditary by Theorem 3.22. Let
$B=\operatorname{End}_{A}(N)$
is right-strongly quasi-hereditary by Theorem 3.22. Let
![]() $e\in B$
be the idempotent corresponding to the direct summand
$e\in B$
be the idempotent corresponding to the direct summand
![]() $A$
of
$A$
of
![]() $N$
. Then
$N$
. Then
![]() $eBe=A$
holds as desired. ◻
$eBe=A$
holds as desired. ◻
Another application of Theorem 3.22 is the following.
Example 3.24. Let
![]() $A$
be an artin algebra. Then there exists the smallest
$A$
be an artin algebra. Then there exists the smallest
![]() $n>0$
such that
$n>0$
such that
![]() $J(A)^{n}=0$
. Let
$J(A)^{n}=0$
. Let
![]() ${\mathcal{C}}_{i}:=\mathsf{add}\bigoplus _{k=1}^{n-i}A/J(A)^{k}$
and
${\mathcal{C}}_{i}:=\mathsf{add}\bigoplus _{k=1}^{n-i}A/J(A)^{k}$
and
![]() $B:=\text{End}_{A}(\bigoplus _{k=1}^{n}A/J(A)^{k})$
. Then
$B:=\text{End}_{A}(\bigoplus _{k=1}^{n}A/J(A)^{k})$
. Then
![]() $B$
has finite global dimension [Reference Auslander2]. Moreover
$B$
has finite global dimension [Reference Auslander2]. Moreover
![]() $B$
is quasi-hereditary [Reference Dlab and Ringel8]. On the other hand,
$B$
is quasi-hereditary [Reference Dlab and Ringel8]. On the other hand,
is a total left rejective chain [Reference Iyama18, Example 2.7.1]. Thus we obtain from Theorem 3.22 that
![]() $B$
is a left-strongly quasi-hereditary algebra. This was independently shown in [Reference Conde6, Reference Ringel22].
$B$
is a left-strongly quasi-hereditary algebra. This was independently shown in [Reference Conde6, Reference Ringel22].
We end this subsection with characterizations of cosemisimple right (resp. left) rejective subcategories. The first one is crucial in the proof of Corollary 3.23(1).
Proposition 3.25. (Iyama [Reference Iyama17, 1.5.1])
Let
![]() ${\mathcal{C}}$
be a Krull–Schmidt category and
${\mathcal{C}}$
be a Krull–Schmidt category and
![]() ${\mathcal{C}}^{\prime }$
a subcategory of
${\mathcal{C}}^{\prime }$
a subcategory of
![]() ${\mathcal{C}}$
. Then
${\mathcal{C}}$
. Then
![]() ${\mathcal{C}}^{\prime }$
is a cosemisimple right (resp. left) rejective subcategory of
${\mathcal{C}}^{\prime }$
is a cosemisimple right (resp. left) rejective subcategory of
![]() ${\mathcal{C}}$
if and only if, for any
${\mathcal{C}}$
if and only if, for any
![]() $X\in \mathsf{ind}{\mathcal{C}}\setminus \mathsf{ind}{\mathcal{C}}^{\prime }$
, there exists a morphism
$X\in \mathsf{ind}{\mathcal{C}}\setminus \mathsf{ind}{\mathcal{C}}^{\prime }$
, there exists a morphism
![]() $\unicode[STIX]{x1D711}:Y\rightarrow X$
(resp.
$\unicode[STIX]{x1D711}:Y\rightarrow X$
(resp.
![]() $\unicode[STIX]{x1D711}:X\rightarrow Y$
) such that
$\unicode[STIX]{x1D711}:X\rightarrow Y$
) such that
![]() $Y\in {\mathcal{C}}^{\prime }$
and
$Y\in {\mathcal{C}}^{\prime }$
and
![]() ${\mathcal{C}}(-,Y)\xrightarrow[{}]{\unicode[STIX]{x1D711}\circ -}{\mathcal{J}}_{{\mathcal{C}}}(-,X)$
(resp.
${\mathcal{C}}(-,Y)\xrightarrow[{}]{\unicode[STIX]{x1D711}\circ -}{\mathcal{J}}_{{\mathcal{C}}}(-,X)$
(resp.
![]() ${\mathcal{C}}(Y,-)\xrightarrow[{}]{-\circ \unicode[STIX]{x1D711}}{\mathcal{J}}_{{\mathcal{C}}}(X,-)$
) is an isomorphism on
${\mathcal{C}}(Y,-)\xrightarrow[{}]{-\circ \unicode[STIX]{x1D711}}{\mathcal{J}}_{{\mathcal{C}}}(X,-)$
) is an isomorphism on
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
Proof. We show the “only if” part. For any
![]() $X\in \mathsf{ind}{\mathcal{C}}\setminus \mathsf{ind}{\mathcal{C}}^{\prime }$
, we take a morphism
$X\in \mathsf{ind}{\mathcal{C}}\setminus \mathsf{ind}{\mathcal{C}}^{\prime }$
, we take a morphism
![]() $\unicode[STIX]{x1D711}:Y\rightarrow X$
such that
$\unicode[STIX]{x1D711}:Y\rightarrow X$
such that
![]() $Y\in {\mathcal{C}}^{\prime }$
and
$Y\in {\mathcal{C}}^{\prime }$
and
![]() ${\mathcal{C}}(-,Y)\xrightarrow[{}]{\unicode[STIX]{x1D711}\circ -}[{\mathcal{C}}^{\prime }](-,X)$
is an isomorphism on
${\mathcal{C}}(-,Y)\xrightarrow[{}]{\unicode[STIX]{x1D711}\circ -}[{\mathcal{C}}^{\prime }](-,X)$
is an isomorphism on
![]() ${\mathcal{C}}$
. This gives a desired morphism since cosemisimplicity of
${\mathcal{C}}$
. This gives a desired morphism since cosemisimplicity of
![]() ${\mathcal{C}}^{\prime }$
implies that
${\mathcal{C}}^{\prime }$
implies that
![]() ${\mathcal{J}}_{{\mathcal{C}}}(-,X)=[{\mathcal{C}}^{\prime }](-,X)$
.
${\mathcal{J}}_{{\mathcal{C}}}(-,X)=[{\mathcal{C}}^{\prime }](-,X)$
.
We show the “if” part. It suffices to prove that
![]() $[{\mathcal{C}}^{\prime }](-,X)={\mathcal{J}}_{{\mathcal{C}}}(-,X)$
for any
$[{\mathcal{C}}^{\prime }](-,X)={\mathcal{J}}_{{\mathcal{C}}}(-,X)$
for any
![]() $X\in \mathsf{ind}{\mathcal{C}}\setminus \mathsf{ind}{\mathcal{C}}^{\prime }$
. For any
$X\in \mathsf{ind}{\mathcal{C}}\setminus \mathsf{ind}{\mathcal{C}}^{\prime }$
. For any
![]() $X\in \mathsf{ind}{\mathcal{C}}\setminus \mathsf{ind}{\mathcal{C}}^{\prime }$
, we take a morphism
$X\in \mathsf{ind}{\mathcal{C}}\setminus \mathsf{ind}{\mathcal{C}}^{\prime }$
, we take a morphism
![]() $\unicode[STIX]{x1D711}:Y\rightarrow X$
such that
$\unicode[STIX]{x1D711}:Y\rightarrow X$
such that
![]() $Y\in {\mathcal{C}}^{\prime }$
and
$Y\in {\mathcal{C}}^{\prime }$
and
![]() ${\mathcal{C}}(-,Y)\xrightarrow[{}]{\unicode[STIX]{x1D711}\circ -}{\mathcal{J}}_{{\mathcal{C}}}(-,X)$
is an isomorphism on
${\mathcal{C}}(-,Y)\xrightarrow[{}]{\unicode[STIX]{x1D711}\circ -}{\mathcal{J}}_{{\mathcal{C}}}(-,X)$
is an isomorphism on
![]() ${\mathcal{C}}$
. Then
${\mathcal{C}}$
. Then
![]() ${\mathcal{J}}_{{\mathcal{C}}}(-,X)\subseteq \text{Im}(\unicode[STIX]{x1D711}\circ -)\subseteq [{\mathcal{C}}^{\prime }](-,X)$
holds. Since
${\mathcal{J}}_{{\mathcal{C}}}(-,X)\subseteq \text{Im}(\unicode[STIX]{x1D711}\circ -)\subseteq [{\mathcal{C}}^{\prime }](-,X)$
holds. Since
![]() $X\not \in {\mathcal{C}}^{\prime }$
, this clearly implies
$X\not \in {\mathcal{C}}^{\prime }$
, this clearly implies
![]() ${\mathcal{J}}_{{\mathcal{C}}}(-,X)=[{\mathcal{C}}^{\prime }](-,X)$
, and hence we have the assertion.◻
${\mathcal{J}}_{{\mathcal{C}}}(-,X)=[{\mathcal{C}}^{\prime }](-,X)$
, and hence we have the assertion.◻
The second one is a reformulation of Proposition 3.25.
Proposition 3.26. (Iyama [Reference Iyama17, Theorem 3.2(3)])
Let
![]() $A$
be a basic artin algebra and
$A$
be a basic artin algebra and
![]() $e$
an idempotent of
$e$
an idempotent of
![]() $A$
. Then
$A$
. Then
![]() $\mathsf{add}eA$
is a cosemisimple right (resp. left) rejective subcategory of
$\mathsf{add}eA$
is a cosemisimple right (resp. left) rejective subcategory of
![]() $\mathsf{proj}A$
if and only if
$\mathsf{proj}A$
if and only if
![]() $(1-e)J(A)\in \mathsf{add}eA$
as a right
$(1-e)J(A)\in \mathsf{add}eA$
as a right
![]() $A$
-module (resp.
$A$
-module (resp.
![]() $J(A)(1-e)\in \mathsf{add}Ae$
as a left
$J(A)(1-e)\in \mathsf{add}Ae$
as a left
![]() $A$
-module).
$A$
-module).
Proof. Applying Proposition 3.25 to
![]() ${\mathcal{C}}:=\mathsf{proj}A$
and
${\mathcal{C}}:=\mathsf{proj}A$
and
![]() ${\mathcal{C}}^{\prime }:=\mathsf{add}eA$
, we have that
${\mathcal{C}}^{\prime }:=\mathsf{add}eA$
, we have that
![]() ${\mathcal{C}}^{\prime }$
is a cosemisimple right rejective subcategory of
${\mathcal{C}}^{\prime }$
is a cosemisimple right rejective subcategory of
![]() ${\mathcal{C}}$
if and only if there exists a morphism
${\mathcal{C}}$
if and only if there exists a morphism
![]() $\unicode[STIX]{x1D711}:Y\rightarrow (1-e)A$
with
$\unicode[STIX]{x1D711}:Y\rightarrow (1-e)A$
with
![]() $Y\in {\mathcal{C}}^{\prime }$
such that
$Y\in {\mathcal{C}}^{\prime }$
such that
is an isomorphism. This means that
![]() $(1-e)J(A)\in {\mathcal{C}}^{\prime }$
holds.◻
$(1-e)J(A)\in {\mathcal{C}}^{\prime }$
holds.◻
3.3 Coreflective subcategories
In this subsection, we study a weaker notion of right (resp. left) rejective subcategories called coreflective (resp. reflective) subcategories. They appeared in the classical theory of localizations of abelian categories [Reference Stenström24]. Let us start with recalling their definitions.
Definition 3.27. (Cf. Stenström [Reference Stenström24])
Let
![]() ${\mathcal{C}}$
be an additive category and
${\mathcal{C}}$
be an additive category and
![]() ${\mathcal{C}}^{\prime }$
a subcategory of
${\mathcal{C}}^{\prime }$
a subcategory of
![]() ${\mathcal{C}}$
. We call
${\mathcal{C}}$
. We call
![]() ${\mathcal{C}}^{\prime }$
a coreflective (resp. reflective) subcategory of
${\mathcal{C}}^{\prime }$
a coreflective (resp. reflective) subcategory of
![]() ${\mathcal{C}}$
if the inclusion functor
${\mathcal{C}}$
if the inclusion functor
![]() ${\mathcal{C}}^{\prime }{\hookrightarrow}{\mathcal{C}}$
admits a right (resp. left) adjoint.
${\mathcal{C}}^{\prime }{\hookrightarrow}{\mathcal{C}}$
admits a right (resp. left) adjoint.
Clearly right (resp. left) rejective subcategories are coreflective (resp. reflective). The following proposition is an analogue of Proposition 3.12.
Proposition 3.28. Let
![]() ${\mathcal{C}}$
be an additive category and
${\mathcal{C}}$
be an additive category and
![]() ${\mathcal{C}}^{\prime }$
a subcategory of
${\mathcal{C}}^{\prime }$
a subcategory of
![]() ${\mathcal{C}}$
. Then the following conditions are equivalent:
${\mathcal{C}}$
. Then the following conditions are equivalent:
(i)
 ${\mathcal{C}}^{\prime }$
is a coreflective (resp. reflective) subcategory of
${\mathcal{C}}^{\prime }$
is a coreflective (resp. reflective) subcategory of
 ${\mathcal{C}}$
.
${\mathcal{C}}$
.(ii) For any
 $X\in {\mathcal{C}}$
, there exists a right (resp. left)
$X\in {\mathcal{C}}$
, there exists a right (resp. left)
 ${\mathcal{C}}^{\prime }$
-approximation
${\mathcal{C}}^{\prime }$
-approximation
 $f_{X}\in {\mathcal{C}}(Y,X)$
(resp.
$f_{X}\in {\mathcal{C}}(Y,X)$
(resp.
 $f^{X}\in {\mathcal{C}}(X,Y)$
) of
$f^{X}\in {\mathcal{C}}(X,Y)$
) of
 $X$
such that
$X$
such that
 ${\mathcal{C}}(-,Y)\xrightarrow[{}]{f_{X}\circ -}{\mathcal{C}}(-,X)\;(\text{resp.}\;{\mathcal{C}}(Y,-)\xrightarrow[{}]{-\circ f^{X}}{\mathcal{C}}(X,-))$
is an isomorphism on
${\mathcal{C}}(-,Y)\xrightarrow[{}]{f_{X}\circ -}{\mathcal{C}}(-,X)\;(\text{resp.}\;{\mathcal{C}}(Y,-)\xrightarrow[{}]{-\circ f^{X}}{\mathcal{C}}(X,-))$
is an isomorphism on
 ${\mathcal{C}}^{\prime }$
.
${\mathcal{C}}^{\prime }$
.
We omit the proof since it is similar to Proposition 3.12.
The following proposition is an analogue of Proposition 3.16.
Proposition 3.29. (Iyama [Reference Iyama17, Theorem 3.2(1)])
Let
![]() $A$
be an artin algebra and
$A$
be an artin algebra and
![]() $e$
an idempotent of
$e$
an idempotent of
![]() $A$
. Then
$A$
. Then
![]() $\mathsf{add}eA$
is a coreflective (resp. reflective) subcategory of
$\mathsf{add}eA$
is a coreflective (resp. reflective) subcategory of
![]() $\mathsf{proj}A$
if and only if
$\mathsf{proj}A$
if and only if
![]() $Ae$
(resp.
$Ae$
(resp.
![]() $eA$
) is a projective right (resp. left)
$eA$
) is a projective right (resp. left)
![]() $eAe$
-module.
$eAe$
-module.
Proof. Assume that
![]() $\mathsf{add}eA$
is a coreflective subcategory of
$\mathsf{add}eA$
is a coreflective subcategory of
![]() $\mathsf{proj}A$
. Then there exists a right
$\mathsf{proj}A$
. Then there exists a right
![]() $(\mathsf{add}eA)$
-approximation
$(\mathsf{add}eA)$
-approximation
![]() $a\in \operatorname{Hom}_{A}(P,A)$
of
$a\in \operatorname{Hom}_{A}(P,A)$
of
![]() $A$
such that
$A$
such that
is an isomorphism. Thus we have an isomorphism
![]() $Ae\cong Pe\in \mathsf{add}(eAe)$
of right
$Ae\cong Pe\in \mathsf{add}(eAe)$
of right
![]() $(eAe)$
-modules and we obtain
$(eAe)$
-modules and we obtain
![]() $Ae\in \mathsf{proj}(eAe)$
.
$Ae\in \mathsf{proj}(eAe)$
.
Conversely, we assume that
![]() $Ae$
is projective as right
$Ae$
is projective as right
![]() $(eAe)$
-modules. Then there exists
$(eAe)$
-modules. Then there exists
![]() $P\in \mathsf{add}eA$
as a right
$P\in \mathsf{add}eA$
as a right
![]() $A$
-module such that
$A$
-module such that
![]() $Pe\cong Ae$
as right
$Pe\cong Ae$
as right
![]() $(eAe)$
-modules. This is induced by a morphism
$(eAe)$
-modules. This is induced by a morphism
![]() $a:P\rightarrow A$
since
$a:P\rightarrow A$
since
![]() $\operatorname{Hom}_{A}(P,A)=\operatorname{Hom}_{eAe}(Pe,Ae)$
(see [Reference Auslander, Reiten and Smalø3, Proposition 2.1(a)]). Since
$\operatorname{Hom}_{A}(P,A)=\operatorname{Hom}_{eAe}(Pe,Ae)$
(see [Reference Auslander, Reiten and Smalø3, Proposition 2.1(a)]). Since
is an isomorphism,
![]() $\mathsf{add}eA$
is coreflective in
$\mathsf{add}eA$
is coreflective in
![]() $\mathsf{proj}A$
.◻
$\mathsf{proj}A$
.◻
Right (resp. left) rejective subcategories are coreflective (resp. reflective) subcategories, but the converse is not true as the following example shows.
Example 3.30. Let
![]() $A$
be the preprojective algebra of type
$A$
be the preprojective algebra of type
![]() $\mathbb{A}_{3}$
. It is defined by the quiver
$\mathbb{A}_{3}$
. It is defined by the quiver
with relations
![]() $\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2},\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FC}_{2}$
. Then
$\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2},\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FC}_{2}$
. Then
![]() $Ae_{3}A$
is not projective as a right
$Ae_{3}A$
is not projective as a right
![]() $A$
-module, but
$A$
-module, but
![]() $Ae_{3}$
is projective as a right
$Ae_{3}$
is projective as a right
![]() $e_{3}Ae_{3}$
-module. Thus
$e_{3}Ae_{3}$
-module. Thus
![]() $\mathsf{add}e_{3}A$
is not a right rejective subcategory of
$\mathsf{add}e_{3}A$
is not a right rejective subcategory of
![]() $\mathsf{proj}A$
by Proposition 3.16, but a coreflective subcategory of
$\mathsf{proj}A$
by Proposition 3.16, but a coreflective subcategory of
![]() $\mathsf{proj}A$
by Proposition 3.29.
$\mathsf{proj}A$
by Proposition 3.29.
We introduce the following analogue of Definition 3.19.
Definition 3.31. Let
![]() ${\mathcal{C}}$
be an additive category. We call a chain of subcategories
${\mathcal{C}}$
be an additive category. We call a chain of subcategories
a coreflective (resp. reflective) chain if
![]() ${\mathcal{C}}_{i}$
is a cosemisimple coreflective (resp. reflective) subcategory of
${\mathcal{C}}_{i}$
is a cosemisimple coreflective (resp. reflective) subcategory of
![]() ${\mathcal{C}}_{i-1}$
for
${\mathcal{C}}_{i-1}$
for
![]() $1\leqslant i\leqslant n$
.
$1\leqslant i\leqslant n$
.
Clearly right (resp. left) rejective chains are coreflective (resp. reflective) chains. The converse is not true as the following example shows.
Example 3.32. Let
![]() $A$
be the preprojective algebra of type
$A$
be the preprojective algebra of type
![]() $\mathbb{A}_{2}$
. It is defined by the quiver
$\mathbb{A}_{2}$
. It is defined by the quiver
with relations
![]() $\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}$
. Then
$\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}$
. Then
is not a right rejective chain, but a coreflective chain of
![]() $\mathsf{proj}A$
. In fact, the conditions (a) and (b) in Definition 3.31 follow from Proposition 3.29 and
$\mathsf{proj}A$
. In fact, the conditions (a) and (b) in Definition 3.31 follow from Proposition 3.29 and
![]() $e_{1}J(A)e_{1}=0$
, respectively. However the condition (a) in Definition 3.19 dose not hold by Proposition 3.16.
$e_{1}J(A)e_{1}=0$
, respectively. However the condition (a) in Definition 3.19 dose not hold by Proposition 3.16.
We are ready to state the following main result in this paper.
Theorem 3.33. In Theorem 3.22, the conditions (i) and (ii) are equivalent to the following condition.
(iii) (3.7) is a heredity chain of
 $A$
and the following chain is a coreflective (resp. reflective) chain of
$A$
and the following chain is a coreflective (resp. reflective) chain of
 $\mathsf{proj}A$
.
$\mathsf{proj}A$
.  $$\begin{eqnarray}\mathsf{proj}A=\mathsf{add}e_{0}A\supset \mathsf{add}e_{1}A\supset \cdots \supset \mathsf{add}e_{n}A=0.\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{proj}A=\mathsf{add}e_{0}A\supset \mathsf{add}e_{1}A\supset \cdots \supset \mathsf{add}e_{n}A=0.\end{eqnarray}$$
To prove Theorem 3.33, we need the following lemma.
Lemma 3.34. Let
![]() $A$
be an artin algebra and
$A$
be an artin algebra and
![]() $I^{\prime }\subset I$
idempotent ideals of
$I^{\prime }\subset I$
idempotent ideals of
![]() $A$
. Let
$A$
. Let
![]() $e$
and
$e$
and
![]() $e^{\prime }$
be idempotents of
$e^{\prime }$
be idempotents of
![]() $A$
such that
$A$
such that
![]() $I=AeA$
and
$I=AeA$
and
![]() $I^{\prime }=Ae^{\prime }A$
. We assume that
$I^{\prime }=Ae^{\prime }A$
. We assume that
![]() $I/I^{\prime }$
is a projective right (resp. left)
$I/I^{\prime }$
is a projective right (resp. left)
![]() $(A/I^{\prime })$
-module and
$(A/I^{\prime })$
-module and
![]() $\text{Tor}_{2}^{A}(A/I,A/I^{\prime })=0$
(resp.
$\text{Tor}_{2}^{A}(A/I,A/I^{\prime })=0$
(resp.
![]() $\text{Tor}_{2}^{A}(A/I^{\prime },A/I)=0$
). If
$\text{Tor}_{2}^{A}(A/I^{\prime },A/I)=0$
). If
![]() $Ae$
(resp.
$Ae$
(resp.
![]() $eA$
) is a projective right (resp. left)
$eA$
) is a projective right (resp. left)
![]() $(eAe)$
-module, then
$(eAe)$
-module, then
![]() $I$
is a projective right (resp. left)
$I$
is a projective right (resp. left)
![]() $A$
-module.
$A$
-module.
Proof. Let
![]() $0\rightarrow K\rightarrow P\rightarrow I\rightarrow 0$
be a projective cover of the right
$0\rightarrow K\rightarrow P\rightarrow I\rightarrow 0$
be a projective cover of the right
![]() $A$
-module
$A$
-module
![]() $I$
. Then
$I$
. Then
![]() $P\in \mathsf{add}eA$
as a right
$P\in \mathsf{add}eA$
as a right
![]() $A$
-module and
$A$
-module and
![]() $K\subset PJ(A)$
hold. Applying the functor
$K\subset PJ(A)$
hold. Applying the functor
![]() $(-)e:\mathsf{mod}A\rightarrow \mathsf{mod}eAe$
, we have a short exact sequence
$(-)e:\mathsf{mod}A\rightarrow \mathsf{mod}eAe$
, we have a short exact sequence
![]() $0\rightarrow Ke\rightarrow Pe\rightarrow Ie\rightarrow 0$
. Since
$0\rightarrow Ke\rightarrow Pe\rightarrow Ie\rightarrow 0$
. Since
![]() $Ie=Ae$
and
$Ie=Ae$
and
![]() $Pe$
are projective
$Pe$
are projective
![]() $(eAe)$
-modules and
$(eAe)$
-modules and
![]() $Ke\subset PeJ(eAe)$
, we have
$Ke\subset PeJ(eAe)$
, we have
![]() $Ke=0$
.
$Ke=0$
.
On the other hand, applying the functor
![]() $-\!\otimes _{A}(A/I^{\prime })$
to the short exact sequence
$-\!\otimes _{A}(A/I^{\prime })$
to the short exact sequence
![]() $0\rightarrow K\rightarrow P\rightarrow I$
, we have an exact sequence
$0\rightarrow K\rightarrow P\rightarrow I$
, we have an exact sequence
where
![]() $\text{Tor}_{1}^{A}(I,A/I^{\prime })=\text{Tor}_{2}^{A}(A/I,A/I^{\prime })=0$
holds by our assumption. Since
$\text{Tor}_{1}^{A}(I,A/I^{\prime })=\text{Tor}_{2}^{A}(A/I,A/I^{\prime })=0$
holds by our assumption. Since
![]() $I/I^{\prime }$
is a projective right
$I/I^{\prime }$
is a projective right
![]() $(A/I^{\prime })$
-module, the sequence splits, and hence
$(A/I^{\prime })$
-module, the sequence splits, and hence
![]() $K/KI^{\prime }$
is a direct summand of
$K/KI^{\prime }$
is a direct summand of
![]() $P/PI^{\prime }$
. On the other hand,
$P/PI^{\prime }$
. On the other hand,
![]() $K\subset PJ(A)$
implies that
$K\subset PJ(A)$
implies that
![]() $K/KI^{\prime }\subset (P/PI^{\prime })J(A)$
. Thus
$K/KI^{\prime }\subset (P/PI^{\prime })J(A)$
. Thus
![]() $K/KI^{\prime }=0$
holds. Consequently,
$K/KI^{\prime }=0$
holds. Consequently,
![]() $K=KI^{\prime }\subset KI=0$
holds as desired.◻
$K=KI^{\prime }\subset KI=0$
holds as desired.◻
We are ready to prove Theorem 3.33.
Proof of Theorem 3.33.
Since (ii)
![]() $\Rightarrow$
(iii) clearly holds, it suffices for us to prove that (iii)
$\Rightarrow$
(iii) clearly holds, it suffices for us to prove that (iii)
![]() $\Rightarrow$
(i). We show this claim by induction on
$\Rightarrow$
(i). We show this claim by induction on
![]() $n$
. If
$n$
. If
![]() $n=1$
, then the assertion holds since
$n=1$
, then the assertion holds since
![]() $H_{0}=A$
is projective as a right
$H_{0}=A$
is projective as a right
![]() $A$
-module.
$A$
-module.
For
![]() $n\geqslant 2$
we proceed by induction. Let
$n\geqslant 2$
we proceed by induction. Let
![]() $e_{i}$
denote the idempotent
$e_{i}$
denote the idempotent
![]() $e_{i}+H_{n-1}$
of
$e_{i}+H_{n-1}$
of
![]() $A/H_{n-1}$
for
$A/H_{n-1}$
for
![]() $0\leqslant i\leqslant n-2$
. First, we claim that
$0\leqslant i\leqslant n-2$
. First, we claim that
is a heredity chain of
![]() $A/H_{n-1}$
such that
$A/H_{n-1}$
such that
![]() $\mathsf{add}e_{i}(A/H_{n-1})$
is a coreflective subcategory of
$\mathsf{add}e_{i}(A/H_{n-1})$
is a coreflective subcategory of
![]() $\mathsf{proj}(A/H_{n-1})$
for
$\mathsf{proj}(A/H_{n-1})$
for
![]() $0\leqslant i\leqslant n-2$
. Since
$0\leqslant i\leqslant n-2$
. Since
![]() $(A/H_{n-1})e_{i}(A/H_{n-1})=H_{i}/H_{n-1}$
for
$(A/H_{n-1})e_{i}(A/H_{n-1})=H_{i}/H_{n-1}$
for
![]() $0\leqslant i\leqslant n-2$
, the above chain is a heredity chain of
$0\leqslant i\leqslant n-2$
, the above chain is a heredity chain of
![]() $A/H_{n-1}$
. Since
$A/H_{n-1}$
. Since
![]() $Ae_{i}\in \mathsf{proj}(e_{i}Ae_{i})$
, we have that
$Ae_{i}\in \mathsf{proj}(e_{i}Ae_{i})$
, we have that
![]() $Ae_{i}\otimes _{e_{i}Ae_{i}}e_{i}(A/H_{n-1})e_{i}=(A/H_{n-1})e_{i}$
is projective as a right
$Ae_{i}\otimes _{e_{i}Ae_{i}}e_{i}(A/H_{n-1})e_{i}=(A/H_{n-1})e_{i}$
is projective as a right
![]() $(e_{i}(A/H_{n-1})e_{i})$
-module. Therefore it follows from Proposition 3.29 that
$(e_{i}(A/H_{n-1})e_{i})$
-module. Therefore it follows from Proposition 3.29 that
![]() $\mathsf{add}e_{i}(A/H_{n-1})$
is a coreflective subcategory of
$\mathsf{add}e_{i}(A/H_{n-1})$
is a coreflective subcategory of
![]() $\mathsf{proj}(A/H_{n-1})$
for
$\mathsf{proj}(A/H_{n-1})$
for
![]() $0\leqslant i\leqslant n-2$
.
$0\leqslant i\leqslant n-2$
.
Now, we deduce from the induction hypothesis that
![]() $H_{i}/H_{n-1}$
is a projective module as a right
$H_{i}/H_{n-1}$
is a projective module as a right
![]() $(A/H_{n-1})$
-module for
$(A/H_{n-1})$
-module for
![]() $0\leqslant i\leqslant n-2$
. For any
$0\leqslant i\leqslant n-2$
. For any
![]() $0\leqslant i\leqslant n-1$
, we obtain from the hypothesis (iii) that
$0\leqslant i\leqslant n-1$
, we obtain from the hypothesis (iii) that
![]() $\mathsf{add}e_{i}A$
is a coreflective subcategory of
$\mathsf{add}e_{i}A$
is a coreflective subcategory of
![]() $\mathsf{proj}A$
, and hence
$\mathsf{proj}A$
, and hence
![]() $Ae_{i}$
is a projective right
$Ae_{i}$
is a projective right
![]() $(e_{i}Ae_{i})$
-module by Proposition 3.29. Thus we have idempotent ideals
$(e_{i}Ae_{i})$
-module by Proposition 3.29. Thus we have idempotent ideals
![]() $H_{n-1},H_{i}$
such that
$H_{n-1},H_{i}$
such that
![]() $H_{n-1}$
is a heredity ideal of
$H_{n-1}$
is a heredity ideal of
![]() $A$
,
$A$
,
![]() $H_{i}/H_{n-1}$
is projective as a right
$H_{i}/H_{n-1}$
is projective as a right
![]() $(A/H_{n-1})$
-module and
$(A/H_{n-1})$
-module and
![]() $Ae_{i}$
is a projective right
$Ae_{i}$
is a projective right
![]() $(e_{i}Ae_{i})$
-module for
$(e_{i}Ae_{i})$
-module for
![]() $0\leqslant i\leqslant n-1$
. Moreover
$0\leqslant i\leqslant n-1$
. Moreover
![]() $\text{Tor}_{2}^{A}(A/H_{i},A/H_{n-1})=\text{Tor}_{2}^{A/H_{n-1}}(A/H_{i},A/H_{n-1})=0$
holds since
$\text{Tor}_{2}^{A}(A/H_{i},A/H_{n-1})=\text{Tor}_{2}^{A/H_{n-1}}(A/H_{i},A/H_{n-1})=0$
holds since
![]() $H_{n-1}$
is a heredity ideal of
$H_{n-1}$
is a heredity ideal of
![]() $A$
. Therefore we deduce from Lemma 3.34 that
$A$
. Therefore we deduce from Lemma 3.34 that
![]() $H_{i}$
is a projective right
$H_{i}$
is a projective right
![]() $A$
-module.◻
$A$
-module.◻
4 Algebras of global dimension at most two
4.1 Algebras of global dimension at most two are right-strongly quasi-hereditary
The aim of this subsection is to prove the following result.
Theorem 4.1. Let
![]() $A$
be an artin algebra such that
$A$
be an artin algebra such that
![]() $\operatorname{gldim}A\leqslant 2$
. Then the following statements hold.
$\operatorname{gldim}A\leqslant 2$
. Then the following statements hold.
(1)
 $A$
is a right-strongly quasi-hereditary algebra.
$A$
is a right-strongly quasi-hereditary algebra.(2) (Iyama [Reference Iyama17, Theorem 3.6]). The category
 $\mathsf{proj}A$
has a total right rejective chain
$\mathsf{proj}A$
has a total right rejective chain  $$\begin{eqnarray}\mathsf{proj}A=\mathsf{add}e_{0}A\supset \mathsf{add}e_{1}A\supset \cdots \supset \mathsf{add}e_{n}A=0.\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{proj}A=\mathsf{add}e_{0}A\supset \mathsf{add}e_{1}A\supset \cdots \supset \mathsf{add}e_{n}A=0.\end{eqnarray}$$
Note that for an artin algebra
![]() $A$
of global dimension at most two, we can similarly construct a total left rejective chain
$A$
of global dimension at most two, we can similarly construct a total left rejective chain
Hence such an algebra is left-strongly quasi-hereditary. However it is not necessarily strongly quasi-hereditary.
We need the following preparation.
Lemma 4.2. (Iyama [Reference Iyama17, Lemma 3.6.1])
Let
![]() $A$
be an artin algebra with
$A$
be an artin algebra with
![]() $\operatorname{gldim}A=m$
where
$\operatorname{gldim}A=m$
where
![]() $2\leqslant m<\infty$
. Then there exist simple right
$2\leqslant m<\infty$
. Then there exist simple right
![]() $A$
-modules
$A$
-modules
![]() $S$
and
$S$
and
![]() $S^{\prime }$
such that the projective dimensions of
$S^{\prime }$
such that the projective dimensions of
![]() $S$
and
$S$
and
![]() $S^{\prime }$
are
$S^{\prime }$
are
![]() $m-1$
and
$m-1$
and
![]() $m$
, respectively.
$m$
, respectively.
Proof. Existence of
![]() $S^{\prime }$
is clear since
$S^{\prime }$
is clear since
![]() $\operatorname{gldim}A$
is supremum of the projective dimensions of simple
$\operatorname{gldim}A$
is supremum of the projective dimensions of simple
![]() $A$
-modules. Let
$A$
-modules. Let
![]() $0\rightarrow X\rightarrow P\rightarrow S^{\prime }\rightarrow 0$
be an exact sequence with a projective
$0\rightarrow X\rightarrow P\rightarrow S^{\prime }\rightarrow 0$
be an exact sequence with a projective
![]() $A$
-module
$A$
-module
![]() $P$
. Then the projective dimension of
$P$
. Then the projective dimension of
![]() $X$
is precisely
$X$
is precisely
![]() $m-1$
. We assume that
$m-1$
. We assume that
![]() $X$
is not simple. Then there exists a proper simple submodule
$X$
is not simple. Then there exists a proper simple submodule
![]() $L$
of
$L$
of
![]() $X$
. Consider the short exact sequence
$X$
. Consider the short exact sequence
Since the projective dimension of
![]() $X$
is
$X$
is
![]() $m-1$
and
$m-1$
and
![]() $\operatorname{gldim}A=m$
, the projective dimension of
$\operatorname{gldim}A=m$
, the projective dimension of
![]() $L$
is at most
$L$
is at most
![]() $m-1$
. We assume that the projective dimension of
$m-1$
. We assume that the projective dimension of
![]() $L$
is strictly less than
$L$
is strictly less than
![]() $m-1$
. Then the projective dimension of
$m-1$
. Then the projective dimension of
![]() $X/L$
is precisely
$X/L$
is precisely
![]() $m-1$
. Therefore we obtain the assertion by replacing
$m-1$
. Therefore we obtain the assertion by replacing
![]() $X$
by
$X$
by
![]() $X/L$
and repeating this argument.◻
$X/L$
and repeating this argument.◻
We are ready to prove the main theorem in this subsection.
Proof of Theorem 4.1.
(2) We show by induction on the number of simple modules. We may assume that
![]() $A$
is basic. Let
$A$
is basic. Let
![]() $n$
be the number of simple
$n$
be the number of simple
![]() $A$
-modules.
$A$
-modules.
Assume that
![]() $n=1$
. Since
$n=1$
. Since
![]() $A$
is simple, the assertion holds.
$A$
is simple, the assertion holds.
For
![]() $n\geqslant 2$
we proceed by induction. If
$n\geqslant 2$
we proceed by induction. If
![]() $A$
is semisimple, then the assertion is obvious. Thus we assume that
$A$
is semisimple, then the assertion is obvious. Thus we assume that
![]() $A$
is non-semisimple. It follows from Lemma 4.2 that there exists a simple
$A$
is non-semisimple. It follows from Lemma 4.2 that there exists a simple
![]() $A$
-module
$A$
-module
![]() $S$
such that the projective dimension of
$S$
such that the projective dimension of
![]() $S$
is precisely one since
$S$
is precisely one since
![]() $\operatorname{gldim}A=1$
or
$\operatorname{gldim}A=1$
or
![]() $\operatorname{gldim}A=2$
. Let
$\operatorname{gldim}A=2$
. Let
![]() $f$
be a primitive idempotent of
$f$
be a primitive idempotent of
![]() $A$
such that
$A$
such that
![]() $S=f(A/J(A))$
. Let
$S=f(A/J(A))$
. Let
![]() $e:=1-f$
and
$e:=1-f$
and
![]() $A^{\prime }:=eAe$
.
$A^{\prime }:=eAe$
.
(i) We claim that
![]() $\mathsf{add}eA$
is a cosemisimple right rejective subcategory of
$\mathsf{add}eA$
is a cosemisimple right rejective subcategory of
![]() $\mathsf{proj}A$
and
$\mathsf{proj}A$
and
![]() $\operatorname{gldim}A^{\prime }\leqslant \operatorname{gldim}A\leqslant 2$
. There exists a short exact sequence
$\operatorname{gldim}A^{\prime }\leqslant \operatorname{gldim}A\leqslant 2$
. There exists a short exact sequence
Since the projective dimension of
![]() $S$
is one, we have
$S$
is one, we have
![]() $fJ(A)\in \mathsf{proj}A$
. Since
$fJ(A)\in \mathsf{proj}A$
. Since
![]() $fA$
is not an indecomposable direct summand of
$fA$
is not an indecomposable direct summand of
![]() $fJ(A)$
, we have
$fJ(A)$
, we have
![]() $fJ(A)\in \mathsf{add}eA$
as a right
$fJ(A)\in \mathsf{add}eA$
as a right
![]() $A$
-module. It follows from Proposition 3.26 that
$A$
-module. It follows from Proposition 3.26 that
![]() $\mathsf{add}eA$
is a cosemisimple right rejective subcategory of
$\mathsf{add}eA$
is a cosemisimple right rejective subcategory of
![]() $\mathsf{proj}A$
. Thus
$\mathsf{proj}A$
. Thus
![]() $A/AeA$
is simple. Since
$A/AeA$
is simple. Since
![]() $\mathsf{add}eA$
is a right rejective subcategory of
$\mathsf{add}eA$
is a right rejective subcategory of
![]() $\mathsf{proj}A$
, it follows from Proposition 3.16 that
$\mathsf{proj}A$
, it follows from Proposition 3.16 that
![]() $\operatorname{gldim}A^{\prime }\leqslant \operatorname{gldim}A\leqslant 2$
.
$\operatorname{gldim}A^{\prime }\leqslant \operatorname{gldim}A\leqslant 2$
.
(ii) We claim that any monomorphism in
![]() $\mathsf{add}eA$
is monic in
$\mathsf{add}eA$
is monic in
![]() $\mathsf{proj}A$
. Let
$\mathsf{proj}A$
. Let
![]() $a:P_{1}\rightarrow P_{0}$
be a monomorphism in
$a:P_{1}\rightarrow P_{0}$
be a monomorphism in
![]() $\mathsf{add}eA$
. Then we have an exact sequence
$\mathsf{add}eA$
. Then we have an exact sequence
in
![]() $\mathsf{mod}A$
. Since
$\mathsf{mod}A$
. Since
![]() $\operatorname{gldim}A\leqslant 2$
, we obtain that
$\operatorname{gldim}A\leqslant 2$
, we obtain that
![]() $P_{2}:=\operatorname{Ker}a\in \mathsf{proj}A$
. Since
$P_{2}:=\operatorname{Ker}a\in \mathsf{proj}A$
. Since
![]() $a$
is a monomorphism in
$a$
is a monomorphism in
![]() $\mathsf{add}eA$
, we have
$\mathsf{add}eA$
, we have
![]() $P_{2}e=\operatorname{Hom}_{A}(eA,P_{2})=0$
. This implies that
$P_{2}e=\operatorname{Hom}_{A}(eA,P_{2})=0$
. This implies that
![]() $P_{2}$
is a module over a simple algebra
$P_{2}$
is a module over a simple algebra
![]() $A/AeA$
. Thus we obtain that
$A/AeA$
. Thus we obtain that
![]() $P_{2}$
is isomorphic to
$P_{2}$
is isomorphic to
![]() $S^{l}$
for some
$S^{l}$
for some
![]() $l\geqslant 0$
. If
$l\geqslant 0$
. If
![]() $l>0$
, then
$l>0$
, then
![]() $S$
is projective as a right
$S$
is projective as a right
![]() $A$
-module. This is a contradiction since the projective dimension of
$A$
-module. This is a contradiction since the projective dimension of
![]() $S$
is one. Therefore we have
$S$
is one. Therefore we have
![]() $l=0$
and
$l=0$
and
![]() $P_{2}=0$
. Thus
$P_{2}=0$
. Thus
![]() $a$
is a monomorphism of
$a$
is a monomorphism of
![]() $A$
-modules, and hence the assertion follows.
$A$
-modules, and hence the assertion follows.
(iii) We claim that any right rejective subcategory
![]() ${\mathcal{C}}$
of
${\mathcal{C}}$
of
![]() $\mathsf{add}eA$
is also right rejective in
$\mathsf{add}eA$
is also right rejective in
![]() $\mathsf{proj}A$
. In fact,
$\mathsf{proj}A$
. In fact,
![]() $A=eA\oplus fA$
and
$A=eA\oplus fA$
and
![]() $\mathsf{add}eA$
has a right
$\mathsf{add}eA$
has a right
![]() ${\mathcal{C}}$
-approximation which is monic in
${\mathcal{C}}$
-approximation which is monic in
![]() $\mathsf{add}eA$
and hence it is also monic in
$\mathsf{add}eA$
and hence it is also monic in
![]() $\mathsf{proj}A$
by (ii). Similarly, composing a right
$\mathsf{proj}A$
by (ii). Similarly, composing a right
![]() ${\mathcal{C}}$
-approximation of
${\mathcal{C}}$
-approximation of
![]() $fJ(A)\in \mathsf{add}eA$
and
$fJ(A)\in \mathsf{add}eA$
and
![]() $\unicode[STIX]{x1D711}:fJ(A){\hookrightarrow}fA$
, we have a right
$\unicode[STIX]{x1D711}:fJ(A){\hookrightarrow}fA$
, we have a right
![]() ${\mathcal{C}}$
-approximation of
${\mathcal{C}}$
-approximation of
![]() $fA$
which is monic in
$fA$
which is monic in
![]() $\mathsf{add}eA$
, and hence in
$\mathsf{add}eA$
, and hence in
![]() $\mathsf{proj}A$
by (ii).
$\mathsf{proj}A$
by (ii).
(iv) We complete the proof by induction on the number of simple
![]() $A$
-modules. By induction hypothesis,
$A$
-modules. By induction hypothesis,
![]() $\mathsf{proj}A^{\prime }\simeq \mathsf{add}eA$
has a total right rejective chain.
$\mathsf{proj}A^{\prime }\simeq \mathsf{add}eA$
has a total right rejective chain.
Composing it with
![]() $\mathsf{proj}A\supset \mathsf{add}eA$
, and apply (iii), we have a total right rejective chain of
$\mathsf{proj}A\supset \mathsf{add}eA$
, and apply (iii), we have a total right rejective chain of
![]() $\mathsf{proj}A$
.
$\mathsf{proj}A$
.
(1) The assertion follows from (2) and Theorem 3.22. ◻
If
![]() $A$
is a strongly quasi-hereditary algebra, then the global dimension of
$A$
is a strongly quasi-hereditary algebra, then the global dimension of
![]() $A$
is at most two [Reference Ringel22]. The converse is not true as the following example shows.
$A$
is at most two [Reference Ringel22]. The converse is not true as the following example shows.
Example 4.3. Let
![]() $Q$
be the quiver
$Q$
be the quiver
![]() $1\leftarrow 2\rightarrow 3$
whose underlying graph is the Dynkin graph
$1\leftarrow 2\rightarrow 3$
whose underlying graph is the Dynkin graph
![]() $\mathbb{A}_{3}$
and
$\mathbb{A}_{3}$
and
![]() $A$
the Auslander algebra of
$A$
the Auslander algebra of
![]() $\mathbf{k}Q$
. Then
$\mathbf{k}Q$
. Then
![]() $A$
is defined by the quiver
$A$
is defined by the quiver

with relations
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}$
,
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}$
,
![]() $\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FF}$
and
$\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FF}$
and
![]() $\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D716}-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}$
. The global dimension of
$\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D716}-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}$
. The global dimension of
![]() $A$
is two. However we cannot construct a strongly heredity chain of
$A$
is two. However we cannot construct a strongly heredity chain of
![]() $A$
. This example can be explained by Theorem 4.6.
$A$
. This example can be explained by Theorem 4.6.
We end this subsection with describing a certain class of artin algebras which is called Ringel self-dual. We recall the following result.
Definition-Theorem 4.4. (Ringel [Reference Ringel21, Theorem 5])
Let
![]() $A$
be a quasi-hereditary algebra and
$A$
be a quasi-hereditary algebra and
![]() $I:=\{1<\cdots <n\}$
. Then there exist the indecomposable
$I:=\{1<\cdots <n\}$
. Then there exist the indecomposable
![]() $A$
-modules
$A$
-modules
![]() $T(1),T(2),\ldots ,T(n)$
such that
$T(1),T(2),\ldots ,T(n)$
such that
![]() $T(i)$
is Ext-injective in
$T(i)$
is Ext-injective in
![]() ${\mathcal{F}}(\unicode[STIX]{x1D6E5})$
and the standard module
${\mathcal{F}}(\unicode[STIX]{x1D6E5})$
and the standard module
![]() $\unicode[STIX]{x1D6E5}(i)$
is embedded to
$\unicode[STIX]{x1D6E5}(i)$
is embedded to
![]() $T(i)$
, with
$T(i)$
, with
![]() $T(i)/\unicode[STIX]{x1D6E5}(i)\in {\mathcal{F}}(\unicode[STIX]{x1D6E5}(j)\mid j<i)$
. Let
$T(i)/\unicode[STIX]{x1D6E5}(i)\in {\mathcal{F}}(\unicode[STIX]{x1D6E5}(j)\mid j<i)$
. Let
![]() $T:=\bigoplus _{i=1}^{n}T(i)$
and
$T:=\bigoplus _{i=1}^{n}T(i)$
and
![]() $R(A):=\operatorname{End}_{A}(T)^{\operatorname{op}}$
. Then
$R(A):=\operatorname{End}_{A}(T)^{\operatorname{op}}$
. Then
![]() $R(A)$
is a quasi-hereditary algebra with respect to the opposite order of
$R(A)$
is a quasi-hereditary algebra with respect to the opposite order of
![]() ${\leqslant}$
. We call
${\leqslant}$
. We call
![]() $R(A)$
a Ringel dual of
$R(A)$
a Ringel dual of
![]() $A$
.
$A$
.
Let
![]() $(A,\leqslant _{A})$
and
$(A,\leqslant _{A})$
and
![]() $(B,\leqslant _{B})$
be quasi-hereditary algebras with simple
$(B,\leqslant _{B})$
be quasi-hereditary algebras with simple
![]() $A$
-modules
$A$
-modules
![]() $\{S_{A}(i)\mid i\in I\}$
and simple
$\{S_{A}(i)\mid i\in I\}$
and simple
![]() $B$
-modules
$B$
-modules
![]() $\{S_{B}(i^{\prime })\mid i^{\prime }\in I^{\prime }\}$
. We say that
$\{S_{B}(i^{\prime })\mid i^{\prime }\in I^{\prime }\}$
. We say that
![]() $(A,\leqslant _{A})$
is isomorphic to
$(A,\leqslant _{A})$
is isomorphic to
![]() $(B,\leqslant _{B})$
as a quasi-hereditary algebra if there exists an algebra isomorphism
$(B,\leqslant _{B})$
as a quasi-hereditary algebra if there exists an algebra isomorphism
![]() $f:A\xrightarrow[{}]{{\sim}}B$
such that the induced map
$f:A\xrightarrow[{}]{{\sim}}B$
such that the induced map
![]() $\unicode[STIX]{x1D711}:I\rightarrow I^{\prime }$
is a poset isomorphism.
$\unicode[STIX]{x1D711}:I\rightarrow I^{\prime }$
is a poset isomorphism.
Let
![]() $(A,\leqslant )$
be a quasi-hereditary algebra and
$(A,\leqslant )$
be a quasi-hereditary algebra and
![]() ${\leqslant}^{\operatorname{op}}$
the opposite order of
${\leqslant}^{\operatorname{op}}$
the opposite order of
![]() ${\leqslant}$
. We say that
${\leqslant}$
. We say that
![]() $A$
is Ringel self-dual if
$A$
is Ringel self-dual if
![]() $(A,\leqslant _{A})$
is isomorphic to
$(A,\leqslant _{A})$
is isomorphic to
![]() $(R(A),\leqslant ^{\operatorname{op}})$
as a quasi-hereditary algebra.
$(R(A),\leqslant ^{\operatorname{op}})$
as a quasi-hereditary algebra.
Corollary 4.5. Let
![]() $A$
be a Ringel self-dual algebra. Then the following conditions are equivalent:
$A$
be a Ringel self-dual algebra. Then the following conditions are equivalent:
(i)
 $A$
has global dimension at most two.
$A$
has global dimension at most two.(ii)
 $A$
is strongly quasi-hereditary.
$A$
is strongly quasi-hereditary.(iii)
 $A$
is right-strongly quasi-hereditary.
$A$
is right-strongly quasi-hereditary.
Proof. (ii)
![]() $\Rightarrow$
(i): This is shown in [Reference Ringel22].
$\Rightarrow$
(i): This is shown in [Reference Ringel22].
(i)
![]() $\Rightarrow$
(iii): This follows from Theorem 4.1 immediately.
$\Rightarrow$
(iii): This follows from Theorem 4.1 immediately.
(iii)
![]() $\Rightarrow$
(ii): Let
$\Rightarrow$
(ii): Let
![]() $A$
be a right-strongly quasi-hereditary algebra. Since the Ringel dual of a right-strongly quasi-hereditary algebra is left-strongly quasi-hereditary with the opposite order [Reference Ringel22, Proposition A.2],
$A$
be a right-strongly quasi-hereditary algebra. Since the Ringel dual of a right-strongly quasi-hereditary algebra is left-strongly quasi-hereditary with the opposite order [Reference Ringel22, Proposition A.2],
![]() $A$
is strongly quasi-hereditary.◻
$A$
is strongly quasi-hereditary.◻
4.2 Strongly quasi-hereditary Auslander algebras
Since the global dimensions of Auslander algebras are at most two, it follows from Theorem 4.1 that each Auslander algebra is right-strongly quasi-hereditary. However it is not necessarily true that each Auslander algebra is strongly quasi-hereditary. The aim of this subsection is to provide the following characterization of Auslander algebras which are strongly quasi-hereditary. Recall that an artin algebra
![]() $A$
is a Nakayama algebra if and only if every indecomposable
$A$
is a Nakayama algebra if and only if every indecomposable
![]() $A$
-module is uniserial (see for example [Reference Auslander, Reiten and Smalø3, Section 4.2]).
$A$
-module is uniserial (see for example [Reference Auslander, Reiten and Smalø3, Section 4.2]).
Theorem 4.6. Let
![]() $A$
be a representation-finite artin algebra and
$A$
be a representation-finite artin algebra and
![]() $B$
the Auslander algebra of
$B$
the Auslander algebra of
![]() $A$
. Then the following conditions are equivalent.
$A$
. Then the following conditions are equivalent.
(i)
 $B$
is strongly quasi-hereditary.
$B$
is strongly quasi-hereditary.(ii)
 $\mathsf{proj}B$
has a rejective chain.
$\mathsf{proj}B$
has a rejective chain.(iii)
 $A$
is a Nakayama algebra.
$A$
is a Nakayama algebra.
To prove Theorem 4.6, we need the following observation.
Lemma 4.7. Let
![]() $A$
be an artin algebra and
$A$
be an artin algebra and
![]() $B$
a factor algebra of
$B$
a factor algebra of
![]() $A$
such that
$A$
such that
![]() $\mathsf{mod}B$
is a cosemisimple subcategory of
$\mathsf{mod}B$
is a cosemisimple subcategory of
![]() $\mathsf{mod}A$
. Then the following statements hold.
$\mathsf{mod}A$
. Then the following statements hold.
(1) Let
 $X$
be an indecomposable
$X$
be an indecomposable
 $A$
-module which does not belong to
$A$
-module which does not belong to
 $\mathsf{mod}B$
. Then
$\mathsf{mod}B$
. Then
 $X$
is a projective–injective
$X$
is a projective–injective
 $A$
-module such that
$A$
-module such that
 $XJ(A)$
is an indecomposable
$XJ(A)$
is an indecomposable
 $B$
-module.
$B$
-module.(2)
 $B$
is a Nakayama algebra if and only if
$B$
is a Nakayama algebra if and only if
 $A$
is a Nakayama algebra.
$A$
is a Nakayama algebra.
Proof. (1) By Proposition 3.25, there exists a morphism
![]() $\unicode[STIX]{x1D711}:Y\rightarrow X$
of
$\unicode[STIX]{x1D711}:Y\rightarrow X$
of
![]() $A$
-modules such that
$A$
-modules such that
![]() $Y\in \mathsf{mod}B$
and
$Y\in \mathsf{mod}B$
and
![]() $\operatorname{Hom}_{A}(-,Y)\xrightarrow[{}]{\unicode[STIX]{x1D711}\circ -}{\mathcal{J}}_{\mathsf{mod}A}(-,X)$
is an isomorphism on
$\operatorname{Hom}_{A}(-,Y)\xrightarrow[{}]{\unicode[STIX]{x1D711}\circ -}{\mathcal{J}}_{\mathsf{mod}A}(-,X)$
is an isomorphism on
![]() $\mathsf{mod}A$
. Then
$\mathsf{mod}A$
. Then
![]() $\unicode[STIX]{x1D711}$
is a minimal right almost split morphism of
$\unicode[STIX]{x1D711}$
is a minimal right almost split morphism of
![]() $X$
in
$X$
in
![]() $\mathsf{mod}A$
. If
$\mathsf{mod}A$
. If
![]() $X$
is not a projective
$X$
is not a projective
![]() $A$
-module, then
$A$
-module, then
![]() $\unicode[STIX]{x1D711}$
is surjective and hence
$\unicode[STIX]{x1D711}$
is surjective and hence
![]() $X\in \mathsf{mod}B$
, a contradiction. Therefore
$X\in \mathsf{mod}B$
, a contradiction. Therefore
![]() $X$
is a projective
$X$
is a projective
![]() $A$
-module, and
$A$
-module, and
![]() $\unicode[STIX]{x1D711}$
is an inclusion map
$\unicode[STIX]{x1D711}$
is an inclusion map
![]() $XJ(A)\rightarrow X$
. Thus
$XJ(A)\rightarrow X$
. Thus
![]() $XJ(A)=Y$
is a
$XJ(A)=Y$
is a
![]() $B$
-module. The dual argument shows that
$B$
-module. The dual argument shows that
![]() $X$
is an injective
$X$
is an injective
![]() $A$
-module, and hence
$A$
-module, and hence
![]() $XJ(A)$
is indecomposable.
$XJ(A)$
is indecomposable.
(2) Since the “if” part is obvious, we prove the “only if” part. Let
![]() $M$
be an indecomposable
$M$
be an indecomposable
![]() $A$
-module which is either projective or injective. We show that
$A$
-module which is either projective or injective. We show that
![]() $M$
is a uniserial
$M$
is a uniserial
![]() $A$
-module. If
$A$
-module. If
![]() $M$
is a
$M$
is a
![]() $B$
-module, then this is clear. Assume that
$B$
-module, then this is clear. Assume that
![]() $M$
is not a
$M$
is not a
![]() $B$
-module. By (1),
$B$
-module. By (1),
![]() $M$
is a projective–injective
$M$
is a projective–injective
![]() $A$
-module such that
$A$
-module such that
![]() $MJ(A)$
is an indecomposable
$MJ(A)$
is an indecomposable
![]() $B$
-module. Since
$B$
-module. Since
![]() $B$
is a Nakayama algebra,
$B$
is a Nakayama algebra,
![]() $MJ(A)$
is uniserial. Hence
$MJ(A)$
is uniserial. Hence
![]() $M$
is also uniserial.◻
$M$
is also uniserial.◻
We are ready to show the main theorem in this subsection.
Proof of Theorem 4.6.
It suffices to show from Theorem 3.22 that (ii) is equivalent to (iii).
(ii)
![]() $\Rightarrow$
(iii): We show by induction on the length
$\Rightarrow$
(iii): We show by induction on the length
![]() $l(A)$
of
$l(A)$
of
![]() $A$
as a right
$A$
as a right
![]() $A$
-module. If
$A$
-module. If
![]() $l(A)=1$
, then this is clear. For
$l(A)=1$
, then this is clear. For
![]() $l(A)\geqslant 2$
we proceed by induction. Since
$l(A)\geqslant 2$
we proceed by induction. Since
![]() $B$
is a strongly quasi-hereditary algebra, it follows from Theorem 3.22 that
$B$
is a strongly quasi-hereditary algebra, it follows from Theorem 3.22 that
![]() $\mathsf{proj}B\simeq \mathsf{mod}A$
has a rejective chain
$\mathsf{proj}B\simeq \mathsf{mod}A$
has a rejective chain
Since
![]() ${\mathcal{C}}_{1}$
is a rejective subcategory of
${\mathcal{C}}_{1}$
is a rejective subcategory of
![]() $\mathsf{mod}A$
, there exists a two-sided ideal
$\mathsf{mod}A$
, there exists a two-sided ideal
![]() $I$
of
$I$
of
![]() $A$
such that
$A$
such that
![]() ${\mathcal{C}}_{1}=\mathsf{mod}(A/I)$
by Proposition 3.14. It follows from the induction hypothesis that
${\mathcal{C}}_{1}=\mathsf{mod}(A/I)$
by Proposition 3.14. It follows from the induction hypothesis that
![]() $A/I$
is a Nakayama algebra. Therefore we obtain from Lemma 4.7(2) that
$A/I$
is a Nakayama algebra. Therefore we obtain from Lemma 4.7(2) that
![]() $A$
is also a Nakayama algebra.
$A$
is also a Nakayama algebra.
(iii)
![]() $\Rightarrow$
(ii): We show by induction on
$\Rightarrow$
(ii): We show by induction on
![]() $l(A)$
. If
$l(A)$
. If
![]() $l(A)=1$
, then the assertion holds. For
$l(A)=1$
, then the assertion holds. For
![]() $l(A)\geqslant 2$
, we prove that
$l(A)\geqslant 2$
, we prove that
![]() $\mathsf{mod}A$
has a rejective chain by induction. Since
$\mathsf{mod}A$
has a rejective chain by induction. Since
![]() $A$
is a Nakayama algebra, there exists an indecomposable projective–injective
$A$
is a Nakayama algebra, there exists an indecomposable projective–injective
![]() $A$
-module
$A$
-module
![]() $P$
. Let
$P$
. Let
![]() $M$
be a direct sum of all indecomposable
$M$
be a direct sum of all indecomposable
![]() $A$
-modules which are not isomorphic to
$A$
-modules which are not isomorphic to
![]() $P$
and
$P$
and
![]() ${\mathcal{C}}_{1}:=\mathsf{add}M$
. Then
${\mathcal{C}}_{1}:=\mathsf{add}M$
. Then
![]() ${\mathcal{C}}_{1}$
is closed under factor modules and submodules. It follows from Proposition 3.14 that there exists a two-sided ideal
${\mathcal{C}}_{1}$
is closed under factor modules and submodules. It follows from Proposition 3.14 that there exists a two-sided ideal
![]() $I$
of
$I$
of
![]() $A$
such that
$A$
such that
![]() ${\mathcal{C}}_{1}=\mathsf{mod}(A/I)$
. On the other hand, we have
${\mathcal{C}}_{1}=\mathsf{mod}(A/I)$
. On the other hand, we have
![]() $\mathsf{ind}(\mathsf{mod}A)\setminus \mathsf{ind}({\mathcal{C}}_{1})=\{P\}$
. Since the inclusion map
$\mathsf{ind}(\mathsf{mod}A)\setminus \mathsf{ind}({\mathcal{C}}_{1})=\{P\}$
. Since the inclusion map
![]() $\unicode[STIX]{x1D711}:PJ(A)\rightarrow P$
gives an isomorphism
$\unicode[STIX]{x1D711}:PJ(A)\rightarrow P$
gives an isomorphism
![]() $\operatorname{Hom}_{A}(-,PJ(A))\xrightarrow[{}]{\unicode[STIX]{x1D711}\circ -}\operatorname{Hom}_{A}(-,P)$
on
$\operatorname{Hom}_{A}(-,PJ(A))\xrightarrow[{}]{\unicode[STIX]{x1D711}\circ -}\operatorname{Hom}_{A}(-,P)$
on
![]() $\mathsf{mod}A$
, we obtain from Proposition 3.25 that
$\mathsf{mod}A$
, we obtain from Proposition 3.25 that
![]() $\mathsf{mod}A/I$
is a cosemisimple right rejective subcategory of
$\mathsf{mod}A/I$
is a cosemisimple right rejective subcategory of
![]() $\mathsf{mod}A$
. Since
$\mathsf{mod}A$
. Since
![]() $l(A)>l(A/I)$
, we obtain from the induction hypothesis that there exists a rejective chain
$l(A)>l(A/I)$
, we obtain from the induction hypothesis that there exists a rejective chain
![]() $\mathsf{mod}(A/I)\supset \cdots \supset {\mathcal{C}}_{i}\supset \cdots \supset 0$
of
$\mathsf{mod}(A/I)\supset \cdots \supset {\mathcal{C}}_{i}\supset \cdots \supset 0$
of
![]() $\mathsf{mod}(A/I)$
. Composing with
$\mathsf{mod}(A/I)$
. Composing with
![]() $\mathsf{mod}A\supset \mathsf{mod}(A/I)$
, we have a rejective chain of
$\mathsf{mod}A\supset \mathsf{mod}(A/I)$
, we have a rejective chain of
![]() $\mathsf{mod}A$
.
$\mathsf{mod}A$
.
The proof is complete.◻
Acknowledgments
The author is greatly indebted to Osamu Iyama for his insightful comments and permission to include detailed proof of results in [Reference Iyama17] in this paper. The author would like to thank Kentaro Wada, Ryoichi Kase and Yasuaki Ogawa for their valuable comments. The author would also like to thank Hyohe Miyachi and Yoshiyuki Kimura for their assistance.