Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-10T01:10:51.279Z Has data issue: false hasContentIssue false
  • English
  • Français

A Sum Connected with Quadratic Residues

Published online by Cambridge University Press:  22 January 2016

L. Carlitz
L. Carlitz*
Affiliation:
Duke University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let p be a prime > 2 and m an arbitrary positive integer; define

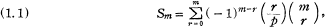
where (r/p) is the Legendre symbol. We consider the problem of finding the highest power of p dividing Sm. A little more generally, if we put

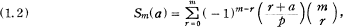
where a is an arbitrary integer, we seek the highest power of p dividing Sm(a). Clearly Sm = Sm(0), and Sm(a) = Sm(b) when a ≡ b (mod p).

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 10 , June 1956 , pp. 1 - 7
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1956

References

[ 1 ] Jordan, C., Calculus of finite differences, second edition, New York, 1947.Google Scholar
[ 2 ] Landau, E., Vorlesungen über Zahlentheorie, vol. 1, Leipzig, 1927.Google Scholar
[ 3 ] Nagell, T., Introduction to number theory, New York, 1951.Google Scholar
[ 4 ] Ward, M., The representation of Stirling’s numbers and Stirling’s polynomials as sums of factorials, American Journal of Mathematics, 56 (1934), pp. 87–95.CrossRefGoogle Scholar