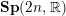Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-13T04:00:37.809Z Has data issue: false hasContentIssue false
  • English
  • Français

SUR LES PAQUETS D’ARTHUR DE $\mathbf{Sp}(2n,\mathbb{R})$ CONTENANT DES MODULES UNITAIRES DE PLUS HAUT POIDS, SCALAIRES

Part of: Lie groups

Published online by Cambridge University Press:  13 June 2019

COLETTE MOEGLIN  and
DAVID RENARD
COLETTE MOEGLIN
Affiliation:
CNRS, Institut mathématique de Jussieu email colette.moeglin@imj-prg.fr
DAVID RENARD
Affiliation:
Centre de mathématiques Laurent Schwartz, École polytechnique email david.renard@polytechnique.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Soit $\unicode[STIX]{x1D70B}$ un module de plus haut poids unitaire du groupe 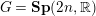$G=\mathbf{Sp}(2n,\mathbb{R})$. On s’intéresse aux paquets d’Arthur contenant $\unicode[STIX]{x1D70B}$. Lorsque le plus haut poids est scalaire, on détermine les paramètres de ces paquets, on établit la propriété de multiplicité 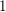$1$ de $\unicode[STIX]{x1D70B}$ dans le paquet, et l’on calcule le caractère 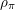$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}}$ (du groupe des composantes connexes du centralisateur du paramètre dans le groupe dual) associé à $\unicode[STIX]{x1D70B}$ et qui joue un grand rôle dans la théorie d’Arthur. On fait de même pour certains modules de plus haut poids unitaires unipotents 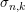$\unicode[STIX]{x1D70E}_{n,k}$, ou bien lorsque le caractère infinitésimal est régulier.

Let $\unicode[STIX]{x1D70B}$ be an irreducible unitary highest weight module for 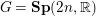$G=\mathbf{Sp}(2n,\mathbb{R})$. We would like to determine the Arthur packets containing $\unicode[STIX]{x1D70B}$. When the highest weight is scalar, we determine the Arthur parameter of these packets, we establish the multiplicity one property of $\unicode[STIX]{x1D70B}$ in the packet and we compute the character 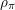$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}}$ (of the group of connected components of the centralizer of 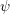$\unicode[STIX]{x1D713}$ in the dual group) associated to $\unicode[STIX]{x1D70B}$ which plays an important role in Arthur’s theory. We also deal with the case of some unipotent unitary highest weight modules 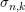$\unicode[STIX]{x1D70E}_{n,k}$, or when the infinitesimal character is regular.

MSC classification

Primary: 22E50: Representations of Lie and linear algebraic groups over local fields
Type
Article
Information
Nagoya Mathematical Journal , Volume 241 , March 2021 , pp. 44 - 124
Check for updates
Copyright
© 2019 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Le second auteur a bénéficié d’une aide de l’Agence nationale de la recherche ANR-13-BS01-0012 FERPLAY.

References

Références

Adams, J., Unitary highest weight modules, Adv. Math. 63(2) (1987), 113–137.10.1016/0001-8708(87)90049-1Google Scholar
Adams, J., Barbasch, D. and Vogan, D. A. Jr, The Langlands Classification and Irreducible Characters for Real Reductive Groups, Progress in Mathematics 104, Birkhäuser Boston, Boston, MA, 1992.10.1007/978-1-4612-0383-4Google Scholar
Adams, J. and Johnson, J. F., Endoscopic groups and packets of nontempered representations, Compositio Math. 64(3) (1987), 271–309.Google Scholar
Arancibia, N., Mœglin, C. and Renard, D., Paquets d’Arthur des groupes classiques et unitaires, cas cohomologique, Annales de la faculté des sciences de Toulouse, Série 6 27(5) (2015), 1023–1105.10.5802/afst.1590Google Scholar
Arthur, J., “Orthogonal and symplectic groups”, in The Endoscopic Classification of Representations, American Mathematical Society Colloquium Publications 61, American Mathematical Society, Providence, RI, 2013.10.1090/coll/061Google Scholar
Barbasch, D., The unitary dual for complex classical Lie groups, Invent. Math. 96(1) (1989), 103–176.10.1007/BF01393972Google Scholar
Chenevier, G. and Lannes, J., Formes automorphes et voisins de Kneser des réseaux de Niemeier, Springer, Switzerland, 2019.Google Scholar
Chenevier, G. and Renard, D., Level one algebraic cusp forms of classical groups of small rank, Mem. Amer. Math. Soc. 237(1121) (2015), v+122.Google Scholar
Enright, T., Howe, R. and Wallach, N., “A classification of unitary highest weight modules”, in Representation Theory of Reductive Groups (Park City, Utah, 1982), Progress in Mathematics 40, Birkhäuser Boston, Boston, MA, 1983, 97–143.10.1007/978-1-4684-6730-7_7Google Scholar
Gan, W. T. and Takeda, S., A proof of the Howe duality conjecture, J. Amer. Math. Soc. 29(2) (2016), 473–493.10.1090/jams/839Google Scholar
Hecht, H. and Schmid, W., Characters, asymptotics and n-homology of Harish-Chandra modules, Acta Math. 151(1–2) (1983), 49–151.10.1007/BF02393204Google Scholar
Howe, R., Transcending classical invariant theory, J. Amer. Math. Soc. 2(3) (1989), 535–552.10.1090/S0894-0347-1989-0985172-6Google Scholar
Igusa, J.-I., On Siegel modular forms of genus two, Amer. J. Math. 84 (1962), 175–200.10.2307/2372812Google Scholar
Jakobsen, H. P., Hermitian symmetric spaces and their unitary highest weight modules, J. Funct. Anal. 52(3) (1983), 385–412.10.1016/0022-1236(83)90076-9Google Scholar
Kashiwara, M. and Vergne, M., On the Segal–Shale–Weil representations and harmonic polynomials, Invent. Math. 44(1) (1978), 1–47.10.1007/BF01389900Google Scholar
Knapp, A. W. and Vogan, D. A. Jr, Cohomological Induction and Unitary Representations, Princeton Mathematical Series 45, Princeton University Press, Princeton, NJ, 1995.10.1515/9781400883936Google Scholar
Kudla, S. S. and Rallis, S., A regularized Siegel–Weil formula: the first term identity, Ann. of Math. (2) 140(1) (1994), 1–80.10.2307/2118540Google Scholar
Matumoto, H., On the representations of Sp(p, q) and SO∗(2n) unitarily induced from derived functor modules, Composito Math. 140(4) (2004), 1059–1096.10.1112/S0010437X03000629Google Scholar
Mœglin, C., Sur certains paquets d’Arthur et involution d’Aubert-Schneider-Stuhler généralisée, Represent. Theory 10 (2006), 86–129.10.1090/S1088-4165-06-00270-6Google Scholar
Mœglin, C., Formes automorphes de carré intégrable non cuspidales, Manuscripta Math. 127(4) (2008), 411–467.10.1007/s00229-008-0205-8Google Scholar
Mœglin, C., “Conjecture d’Adams pour la correspondance de Howe et filtration de Kudla”, in Arithmetic Geometry and Automorphic Forms, Adv. Lect. Math. (ALM) 19, Int. Press, Somerville, MA, 2011, 445–503.Google Scholar
Mœglin, C., “Paquets d’Arthur spéciaux unipotents aux places archimédiennes et correspondance de Howe”, in Representation Theory, Number Theory, and Invariant Theory, Progress in Mathematics 323, Birkhäuser/Springer, Cham, 2017, 469–502.10.1007/978-3-319-59728-7_15Google Scholar
Mœglin, C. and Renard, D., “Sur les paquets d’Arthur aux places réelles, translation”, in Geometric Aspects of the Trace Formula, Simons Symposia, Springer.Google Scholar
Mœglin, C. and Renard, D., Sur les paquets d’Arthur des groupes classiques réels, J. Eur. Math. Soc. (à paraître).Google Scholar
Mœglin, C. and Waldspurger, J.-L., “Une paraphrase de l’Écriture [A paraphrase of Scripture]”, in Spectral Decomposition and Eisenstein Series, Cambridge Tracts in Mathematics 113, Cambridge University Press, Cambridge, 1995.10.1017/CBO9780511470905Google Scholar
Nishiyama, K., Ochiai, H. and Taniguchi, K., Bernstein degree and associated cycles of Harish-Chandra modules—Hermitian symmetric case, Astérisque (273) (2001), 13–80. Nilpotent orbits, associated cycles and Whittaker models for highest weight representations.Google Scholar
Oda, T., An explicit integral representation of Whittaker functions on Sp(2; R) for the large discrete series representations, Tohoku Math. J. (2) 46(2) (1994), 261–279.10.2748/tmj/1178225761Google Scholar
Ohta, T., The closures of nilpotent orbits in the classical symmetric pairs and their singularities, Tohoku Math. J. (2) 43(2) (1991), 161–211.10.2748/tmj/1178227492Google Scholar
Rallis, S., On the Howe duality conjecture, Compositio Math. 51(3) (1984), 333–399.Google Scholar
Shelstad, D., “On elliptic factors in real endoscopic transfer I”, in Representations of Reductive Groups, Progress in Mathematics 312, Birkhäuser/Springer, Cham, 2015, 455–504.10.1007/978-3-319-23443-4_17Google Scholar
Sun, B. and Zhu, C.-B., Conservation relations for local theta correspondence, J. Amer. Math. Soc. 28(4) (2015), 939–983.10.1090/S0894-0347-2014-00817-1Google Scholar
Taïbi, O., Dimensions of spaces of level one automorphic forms for split classical groups using the trace formula, Ann. Sci. Éc. Norm. Supér. (4) 50(2) (2017), 269–344.10.24033/asens.2321Google Scholar
Taïbi, O., Arthur’s multiplicity formula for certain inner forms of special orthogonal and symplectic groups, J. Eur. Math. Soc. (JEMS) 21(3) (2019), 839–871.10.4171/JEMS/852Google Scholar
Trapa, P. E., Annihilators and associated varieties of A q(𝜆) modules for U(p, q), Compositio Math. 129(1) (2001), 1–45.10.1023/A:1013115223377Google Scholar
Trapa, P. E., Richardson orbits for real classical groups, J. Algebra 286(2) (2005), 361–385.10.1016/j.jalgebra.2003.07.027Google Scholar
Tsushima, R., “An explicit dimension formula for the spaces of generalized automorphic forms with respect to Sp(2, Z)”, in Automorphic Forms of Several Variables (Katata, 1983), Progress in Mathematics 46, Birkhäuser Boston, Boston, MA, 1984, 378–383.Google Scholar
Tsuyumine, S., On the Siegel modular function field of degree three, Compositio Math. 63(1) (1987), 83–98.Google Scholar
Vogan, D. A. Jr, Representations of Real Reductive Lie Groups, Progress in Mathematics 15, Birkhäuser, Boston, MA, 1981.Google Scholar
Vogan, D. A. Jr, “Irreducibility of discrete series representations for semisimple symmetric spaces”, in Representations of Lie Groups, Kyoto, Hiroshima, 1986, Adv. Stud. Pure Math. 14, Academic Press, Boston, MA, 1988, 191–221.Google Scholar
Vogan, D. A. Jr, “Associated varieties and unipotent representations”, in Harmonic Analysis on Reductive Groups (Brunswick, ME, 1989), Progress in Mathematics 101, Birkhäuser Boston, Boston, MA, 1991, 315–388.10.1007/978-1-4612-0455-8_17Google Scholar
Vogan, D. A. Jr and Zuckerman, G. J., Unitary representations with nonzero cohomology, Compositio Math. 53(1) (1984), 51–90.Google Scholar
Waldspurger, J.-L., “Démonstration d’une conjecture de dualité de Howe dans le cas p-adique, p≠2”, in Festschrift in Honor of I. I. Piatetski-Shapiro on the Occasion of His Sixtieth Birthday, Part I (Ramat Aviv, 1989), Israel Math. Conf. Proc. 2, Weizmann, Jerusalem, 1990, 267–324.Google Scholar
Wallach, N. R., Generalized Whittaker vectors for holomorphic and quaternionic representations, Comment. Math. Helv. 78(2) (2003), 266–307.10.1007/s000140300012Google Scholar
Yamana, S., L-functions and theta correspondence for classical groups, Invent. Math. 196(3) (2014), 651–732.10.1007/s00222-013-0476-xGoogle Scholar
Zhu, C.-B., Representations with scalar K-types and applications, Israel J. Math. 135 (2003), 111–124.10.1007/BF02776052Google Scholar