Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-13T02:27:57.985Z Has data issue: false hasContentIssue false
  • English
  • Français

Sur l’unicité du cône convexe divisible relatif au noyau de convolution de Hunt défini par l’opérateur différentiel

Published online by Cambridge University Press:  22 January 2016

Masayuki Itô
Masayuki Itô*
Affiliation:
Université de Nagoya
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Dans toute la suite Rn désignera l’espace euclidien à dimension n(≧ 1). Pour un point x = x1, x2, … xn) de Rn, on note |x| = 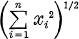et la coordonnée sphérique dans Rn désignera (r, α).

Rappelons qu’un noyau de convolution N sur Rn est une mesure (de Radon) positive dans Rn dans la théorie du potentiel. Pour une mesure réelle μ dans Rn, N * μ s’appelle le N-potentiel de μ dès que cette convolution est définie au sens des mesures. On connaît bien que, dans la théorie du potentiel, les noyaux de convolution de Hunt possédent les propriétés définitives.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 65 , March 1977 , pp. 157 - 182
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1977

References

Bibliographie

[1] Choquet, G. et Deny, J.: Aspects linéaires de la théorie du potentiel, Noyaux de composition satisfaisant au principe du balayage sur tout ouvert, C. R. Acad. Sci. Paris, 250 (1960), p. 4260–4262.Google Scholar
[2] Deny, J.: Noyaux de convolution de Hunt et noyaux associés à une famille fondamentale, Ann. Inst. Fourier, 12 (1962), p. 643–667.CrossRefGoogle Scholar
[3] Herz, C. S.: Analyse harmonique à plusieurs variables, Sém. Math. d’Orsay, 1965/66.Google Scholar
[4] Itô, M.: Sur le principe de domination pour les noyaux de convolution, Nagoya Math. J., 50 (1973), p. 149–173.CrossRefGoogle Scholar
[5] Itô, M.: Une caracterisation du principe de domination pour les noyaux de convolution, Japan. J. Math., 1 (1975), p. 5–35.CrossRefGoogle Scholar
[6] Itô, M.: Sur les cônes convexes de Riesz et les noyaux de convolution complètement sous-harmoniques, Nagoya Math. J., 55 (1974), p. 111–144.CrossRefGoogle Scholar
[7] Itô, M.: Sur L’unicuté du cône convexe divisible constitué par de noyaux de convolution de Dirichlet, Nagoya Math. J., 57 (1975), p. 127–152.CrossRefGoogle Scholar
[8] Widder, D.: The Laplace Transform, Princeton Univ. Press, Princeton, 1948.Google Scholar