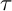Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2025-01-01T05:12:18.407Z Has data issue: false hasContentIssue false
  • English
  • Français

$\tau $-PERPENDICULAR WIDE SUBCATEGORIES

Part of: Representation theory of rings and algebras

Published online by Cambridge University Press:  22 August 2023

ASLAK BAKKE BUAN Open the ORCID record for ASLAK BAKKE BUAN [Opens in a new window]  and
ERIC J. HANSON Open the ORCID record for ERIC J. HANSON [Opens in a new window]
ASLAK BAKKE BUAN
Affiliation:
Department of Mathematical Sciences Norwegian University of Science and Technology (NTNU) 7491 Trondheim, Norway aslak.buan@ntnu.no
ERIC J. HANSON*
Affiliation:
Department of Mathematical Sciences Norwegian University of Science and Technology (NTNU) 7491 Trondheim, Norway
*
hanson.eric@uqam.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 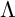$\Lambda $ be a finite-dimensional algebra. A wide subcategory of 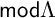$\mathsf {mod}\Lambda $ is called left finite if the smallest torsion class containing it is functorially finite. In this article, we prove that the wide subcategories of $\mathsf {mod}\Lambda $ arising from 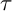$\tau $-tilting reduction are precisely the Serre subcategories of left-finite wide subcategories. As a consequence, we show that the class of such subcategories is closed under further 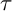$\tau $-tilting reduction. This leads to a natural way to extend the definition of the “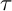$\tau $-cluster morphism category” of 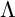$\Lambda $ to arbitrary finite-dimensional algebras. This category was recently constructed by Buan–Marsh in the 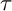$\tau $-tilting finite case and by Igusa–Todorov in the hereditary case.

Keywords

τ-tilting theoryperpendicular categoryτ-tilting reductionτ-cluster morphism categories

MSC classification

Primary: 16G10: Representations of Artinian rings 16G20: Representations of quivers and partially ordered sets
Type
Article
Information
Nagoya Mathematical Journal , Volume 252 , December 2023 , pp. 959 - 984
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by the Norwegian Research Council (Grant No. FRINAT 301375).

References

Adachi, T., Iyama, O., and Reiten, I., $\tau$ -tilting theory , Compos. Math. 150 (2014), 415–452.10.1112/S0010437X13007422CrossRefGoogle Scholar
Asai, S., Semibricks , Int. Math. Res. Not. 2020 (2020), no. 16, 4993–5054.10.1093/imrn/rny150CrossRefGoogle Scholar
Asai, S. and Pfeifer, C., Wide subcategories and lattices of torsion classes , Algebr. Represent. Theory 25 (2022), 1611–1629.10.1007/s10468-021-10079-1CrossRefGoogle Scholar
Auslander, M. and Smalø, S. O., Almost split sequences in subcategories , J. Algebra 69 (1981), 426–454, Addendum: J. Algebra 71 (1981), 592–594.10.1016/0021-8693(81)90214-3CrossRefGoogle Scholar
Barnard, E., Carroll, A.T., and Zhu, S., Minimal inclusions of torsion classes , Algebraic Combin. 2 (2019), 879–901.10.5802/alco.72CrossRefGoogle Scholar
Barnard, E., Todorov, G., and Zhu, S., Dynamical combinatorics and torsion classes , J. Pure Appl. Algebra 225 (2021), 106642.10.1016/j.jpaa.2020.106642CrossRefGoogle Scholar
Børve, E. D., Two-term silting and $\tau$ -cluster morphism categories, preprint, 2021. https://arxiv.org/abs/2110.03472.Google Scholar
Brenner, S. and Butler, M. C. R., “Generalizations of the Berstein–Gelfand–Ponomarev reflection functors,” in Representation Theory II (Proc. Second Internat. Conf., Carleton Univ., Ottawa, Ont., 1979) (Berlin–New York), Lecture Notes in Mathematics, 832, Springer, Berlin, 1980, 103–169.10.1007/BFb0088461CrossRefGoogle Scholar
Buan, A. B. and Marsh, B. R., A category of wide subcategories , Int. Math. Res. Not. 2021 (2021), no. 13, 10278–10338.10.1093/imrn/rnz082CrossRefGoogle Scholar
Buan, A. B. and Marsh, B. R., $\tau$ -exceptional sequences , J. Algebra 585 (2021), 36–68.10.1016/j.jalgebra.2021.04.038CrossRefGoogle Scholar
Demonet, L., Iyama, O., Reading, N., Reiten, I., and Thomas, H., Lattice theory of torsion classes: Beyond $\tau$ -tilting theory , Trans. Amer. Math. Soc. Ser. B 10 (2023), 542–612.10.1090/btran/100CrossRefGoogle Scholar
Enomoto, H., Rigid modules and ICE-closed subcategories in quiver representations , J. Algebra 594 (2022), 364–388.10.1016/j.jalgebra.2021.12.008CrossRefGoogle Scholar
Geigle, W. and Lenzing, H., Perpendicular categories with applications to representations and sheaves , J. Algebra 144 (1991), 273–343.10.1016/0021-8693(91)90107-JCrossRefGoogle Scholar
Hanson, E. J. and Igusa, K., $\tau$ -cluster morphism categories and picture groups , Comm. Algebra 49 (2021), 4376–4415.10.1080/00927872.2021.1921184CrossRefGoogle Scholar
Happel, D., Reiten, I., and Smalø, S. O., Tilting in abelian categories and quasitilted algebras , Mem. Amer. Math. Soc. 120 (1996), no. 575, 1–88.Google Scholar
Hovey, M., Classifying subcategories of modules , Trans. Amer. Math. Soc. 353 (2001), no. 8, 3181–3191.10.1090/S0002-9947-01-02747-7CrossRefGoogle Scholar
Igusa, K., The category of noncrossing partitions, https://arxiv.org/abs/1411.0196.Google Scholar
Igusa, K. and Todorov, G., Signed exceptional sequences and the cluster morphism category, preprint, 2014. https://arxiv.org/abs/1706.02041.Google Scholar
Igusa, K., Todorov, G., and Weyman, J., Picture groups of finite type and cohomology in type $A$ , preprint, 2014. https://arxiv.org/abs/1609.02636.Google Scholar
Ingalls, C. and Thomas, H., Noncrossing partitions and representations of quivers , Compos. Math. 145 (2009), 1533–1562.10.1112/S0010437X09004023CrossRefGoogle Scholar
Iyama, O. and Yang, D., Silting reduction and Calabi-Yau reduction of triangulated categories , Trans. Amer. Math. Soc. 370 (2018), no. 11, 7861–7898.10.1090/tran/7213CrossRefGoogle Scholar
Jasso, G., Reduction of $\tau$ -tilting modules and torsion pairs , Int. Math. Res. Not. 2015 (2015), no. 16, 7190–7237.10.1093/imrn/rnu163CrossRefGoogle Scholar
Marks, F. and Šťovíček, J., Torsion classes, wide subcategories, and localisations , Bull. Lond. Math. Soc. 49 (2017), 405–416.CrossRefGoogle Scholar
Ringel, C. M., “The Catalan combinatorics of the hereditary Artin algebras,” in Recent Developments in Representation Theory, Contemporary Mathematics, 2, Amer. Math. Soc., Providence, RI, 2016, 51–177.10.1090/conm/673/13490CrossRefGoogle Scholar
Smalø, S. O., Torsion theories and tilting modules , Bull. Lond. Math. Soc. 16 (1984), 518–522.10.1112/blms/16.5.518CrossRefGoogle Scholar
Yurikusa, T., Wide subcategories are semistable , Documenta Math. 23 (2018), 35–47.10.4171/dm/612CrossRefGoogle Scholar