Hostname: page-component-6bb9c88b65-zjgpb Total loading time: 0 Render date: 2025-07-28T01:31:27.388Z Has data issue: false hasContentIssue false
  • English
  • Français

Theta Functions and Abelian Varieties over Valuation Fields of Rank one I

Published online by Cambridge University Press:  22 January 2016

Hisasi Morikawa
Hisasi Morikawa*
Affiliation:
Mathematical Institute, Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

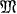We shall denote by the Z-module of integral vectors of dimension 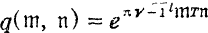r, by T a symmetric complex matrix with positive definite imaginary part and by g the variable vector. If we put and 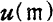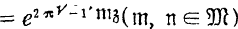the fundamental theta function 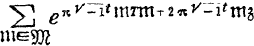is expressed in the form: 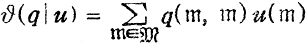as a series in 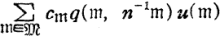q and u. Other theta functions in the classical theory are derived from the fundamental theta function by translating the origin and making sums and products, so these theta functions are also expressed in the form: as series of 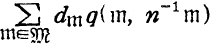q and u. Moreover the coefficients in the relations of theta functions are also expressed in the form: as series in q.

Information

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 20 , June 1962 , pp. 1 - 27
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1962

References

[ 1 ] Albert, A., On involutorial algebras, Proc. Nat. Acad. Sci. U.S.A. Vol. 4, No. 7 (1955), p. 480–482.Google Scholar
[ 2 ] Lang, S., Abelian varieties, (1959).Google Scholar
[ 3 ] Rosenlicht, M., Basic theorems on algebraic groups, Amer. J. Math. Vol. 78, No. 2 (1956), p. 401–443.CrossRefGoogle Scholar
[ 4 ] Serre, P., Groupes algébriques et corpes de classes, 1959 (Paris).Google Scholar
[ 5 ] Weil, A., On algebraic groups and homogeneous spaces, Amer. J. Math. Vol. 77, No. 3 (1955), p. 493–512.Google Scholar
[ 6 ] Weil, A., On the projective embedding of abelian varieties, in the volume in honor of S. Lefschetz, Princeton (1957).Google Scholar