No CrossRef data available.
Article contents
The three-separated-arc property of the modular function
Published online by Cambridge University Press: 22 January 2016
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let D be the open unit disk and Γ be the unit circle in the complex plane, and denote the Riemann sphere by Ω. If f(z) is a function defined on D with values belonging to Ω, if ζ ∈Γ, and if Λ is an arc at ζ then C∈(f, ζ) denotes the cluster set of f at ζ along Λ. If there exist three mutually exclusive arcs Λ1, Λ2, Λ3 at ζ such that
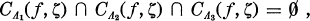
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1976
References
[1]
Belna, C.L., Intersections of arc-cluster sets for meromorphic functions, Nagoya Math. J.
40 (1970), 213–220.CrossRefGoogle Scholar


