TILINGS OF THE SPHERE BY CONGRUENT QUADRILATERALS II: EDGE COMBINATION 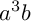$a^3b$ WITH RATIONAL ANGLES

Abstract

Edge-to-edge tilings of the sphere by congruent quadrilaterals are completely classified in a series of three papers. This second one applies the powerful tool of trigonometric Diophantine equations to classify the case of 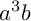$a^3b$-quadrilaterals with all angles being rational degrees. There are 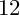$12$ sporadic and 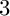$3$ infinite sequences of quadrilaterals admitting the two-layer earth map tilings together with their modifications, and 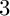$3$ sporadic quadrilaterals admitting 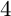$4$ exceptional tilings. Among them only three quadrilaterals are convex. New interesting non-edge-to-edge triangular tilings are obtained as a byproduct.

1 Introduction

In an edge-to-edge tiling of the sphere by congruent quadrilaterals, the tile can only have four edge arrangements [10], [14]: $a^2bc,a^2b^2,a^3b,a^4$ . Sakano and Akama [13] classified tilings for $a^2b^2$ and $a^4$ via Ueno and Agaoka’s [15] list of triangular tilings. Tilings for $a^2bc$ are classified in the first paper [10] of this series via the methods in [2], [16]–[18] developed for pentagonal tilings. This second paper classifies tilings for $a^3b$ with all angles being rational multiples of $\pi $ (such quadrilaterals will be simply called rational hereafter). We then classify tilings for $a^3b$ with some irrational angle in the third paper [11] to complete the classification.

Recall that Coolsaet [4] classified convex rational quadrilaterals with three equal sides into $7$ infinite classes and $29$ sporadic examples. Akama and van Cleemput [1] initiated some explorations of degree $3$ vertex types and certain forbidden cases for type $a^3b$ , assuming also convexity.

An $a^3b$ -quadrilateral is given by Figure 1, with normal edge a, thick edge $b,$ and angles $\alpha ,\beta ,\gamma ,\delta $ as indicated. The second picture is the mirror image or flip of the first. The angles determine the orientation. Conversely, the edge lengths and the orientation also determine the angles. So we may present the tiling by shading instead of indicating all angles. Throughout this paper, an $a^3b$ -tiling is always an edge-to-edge tiling of the sphere by congruent simple quadrilaterals in Figure 1, such that all vertices have degree $\ge 3$ .

Figure 1 Quadrilaterals with the edge combination $a^3b$ .

The first paper [10] of this series constructed a two-parameter family of two-layer earth map tilings by $a^2bc$ -quadrilaterals. The 3D picture in Figure 2 shows an example: One time zone (consisting of two tiles) is outlined by the yellow line, and a cycle of $12$ repeating time zones cover the sphere. All $a^2$ -angles appear at the north/south poles. The $24$ middle points of all b-edges and c-edges distribute evenly on the equator with spacing $\frac {\pi }{12}$ .

Figure 2 $a^2bc$ -quadrilateral and a two-layer earth map tiling $T(24 \alpha \beta \delta , 2\gamma ^{12})$ .

We use $\alpha ^k\beta ^l\gamma ^m\delta ^n$ to mean a vertex having k copies of $\alpha $ , l copies of $\beta $ , etc. The angle-wise vertex combination(s), abbreviated as AVC, is the collection of all vertices in a tiling. Then the notation $T(24 \alpha \beta \delta , 2\gamma ^{12})$ means the tiling has exactly $24$ vertices $\alpha \beta \delta $ and $2$ vertices $\gamma ^{12}$ , and is uniquely determined by them. In general, there may exist several different tilings with the same set of vertices.

The $a^2bc$ -quadrilateral in Figure 2 reduces to the $a^3b$ -quadrilateral in Figure 1 when $c=a$ , and it is natural to expect one-parameter families of two-layer earth map $a^3b$ -tilings. The following main theorem of this paper shows that most rational $a^3b$ -tilings are indeed two-layer earth map tilings.

Theorem. There are $15$ sporadic and $3$ infinite sequences of rational quadrilaterals which admit $a^3b$ -tilings (Tables 1 and 2). Except the last three sporadic cases, they are all two-layer earth map tilings $T(f\alpha \beta \delta ,2\gamma ^{\frac {f}{2}})$ for some even integers $f\ge 6$ , together with their modifications when $\beta $ is an integer multiple of $\gamma $ . The total number $\mathcal {Q}(f)$ of quadrilaterals in Tables 1 and 2 and their total number $\mathcal {T}(f)$ of different tilings are:

In Tables 1 and 2, the angles and edge lengths are expressed in units of $\pi $ , and the last column counts all vertices and also all different tilings when they are not uniquely determined by the vertices. All exact and numerical geometric data are provided in the appendix. A rational fraction, such as $\alpha =\frac {2}{9}$ , means the precise value $\frac {2\pi }{9} $ . A decimal expression, such as $a\approx 0.3918$ , means an approximate value $0.3918\pi \le a < 0.3919\pi $ . We put $\pi $ back in any trigonometric functions to avoid confusion.

Table 1 Fifteen sporadic quadrilaterals and their tilings

Table 2 Three infinite sequences of quadrilaterals and their tilings

Figure 3 Four exceptional tilings with $f=16,16,36,36$ .

Four exceptional tilings for the last three sporadic quadrilaterals in Table 1 ( $f=16,16, 36,36$ ) are shown in Figure 3. The first three tilings have repeated time zones which could be generalized combinatorially. But the quadrilaterals only exist for some particular f due to geometric constraint. We remark that the last tiling ( $f=36$ ) is the only tiling, among all edge-to-edge triangular, quadrilateral, pentagonal tilings of the sphere, which has no apparent relation with any platonic solids or earth map tilings.

1.1 Modifications of special two-layer earth map $a^3b$ -tilings

Once all angles are fixed, there are only finitely many combinations of them summing to $2$ or form a vertex in the tiling. Then one may apply brute-force trial-and-error to find all tilings. However, the following hindsight can help us to understand most tilings in a constructive way.

It turns out that a two-layer earth map $a^3b$ -tiling $T(f\alpha \beta \delta ,2\gamma ^{ \frac {f}{2}})$ admits some modification if and only if $\beta $ is an integer multiple of $\gamma $ . An authentic 3D picture for a two-layer earth map tiling is shown in the left of Figure 4. The structure of any two-layer earth map tiling is shown in Lemma 2.10. When $\beta =m\gamma <1$ , m continuous time zones ( $2m$ tiles) form a dumb-bell like hexagon enclosed by six a-edges in the first picture of Figure 5. Simply flip along the middle vertical line $L_1$ (or equivalently along the middle horizontal line), and one gets a new tiling of the sphere with different vertices. This is called the first basic flip modification. When $\alpha +\delta =m\gamma \le 1$ , we get the second basic flip modification in the right of Figure 5.

Figure 4 Two very different tilings of Case $(1,6,2,3)/5$ in Table 2.

Figure 5 Two basic flip modifications for certain two-layer earth map tilings.

A closer look at the inner and outer sides of this hexagon reveals that these two flips are essentially the same: $\alpha +\delta =m\gamma $ is equivalent to $\beta =(\frac {f}{2}-m)\gamma $ , and the sphere is divided by the six a-edges into two complementary hexagons, either of which may be flipped. However, it is more convenient to flip the smaller one so that we can flip several separated regions to get more tilings. So we still use both basic flips in Figure 5 but assuming afterwards that $m\le \frac {f}{4}$ . Case $(3,20,4,13)/18$ of Table 1 and some sub-sequence of each infinite sequence of Table 2 admit two or three basic flips.

Figure 6 shows four different flips of the two-layer earth map tiling in the third case of Table 2 with $f=14$ tiles. Flipping once, we get the first picture. Flipping twice, we get the second and third pictures when the space between two flips is $0$ or $1$ time zone. Flipping three times, we get the fourth picture.

Figure 6 Four flip modifications for Case $(1,4,2,9)/7$ in Table 2.

For Case $(\frac 2f,\frac {4f-4}{3f},\frac {4}{f},\frac {2f-2}{3f})$ with $f=6k+4\,(k\ge 1)$ , there is another kind of modification giving three more tilings, and we will explain it later using Figures 26 and 30. An authentic $3$ D picture for such a new tiling with $f=10$ is shown in the right of Figure 4.

1.2 Non-edge-to-edge triangular tilings

When any angle of the quadrilateral is $1$ , it degenerates to a triangle as shown in the first two pictures of Figure 7. Then the first infinite sequence and two sporadic cases with $f=6,16$ produce many new examples of non-edge-to-edge triangular tilings.

Figure 7 The degenerate and subdivision ways to get triangular tilings.

The second infinite sequence of quadrilaterals satisfy $\gamma =2\alpha ,\beta =2\delta $ and can be subdivided into three congruent triangles (observed first in [4]) as shown in the third picture of Figure 7, which also induce new non-edge-to-edge triangular tilings. Note that the sporadic case with $f=16$ admits such subdivision too, but inducing only some edge-to-edge triangular tiling.

These are new examples, comparing to early explorations of non-edge-to-edge triangular tilings in [5]–[9].

1.3 Outline of the paper

The classification for $a^2bc$ in [10] is mainly the analysis around a special tile. However, $a^3b$ is handled by a new efficient method, different from all methods developed for triangular and pentagonal tilings. While the cost is to solve some trigonometric Diophantine equations, the idea behind this new method is very simple: too many linearly independent vertex types in a tiling would force all angles to be rational, or the vertex types must be very limited. This paper will identify all rational $a^3b$ -quadrilaterals suitable for tiling. Then the third of our series (see [11]) handles the irrational angle case in a fast way due to strong constraints on vertex types.

This paper is organized as follows: Section 2 includes general results from [10] and some technical results specific to $a^3b$ . Section 3 looks for all possible tilings from Coolsaet’s list of convex rational $a^3b$ -quadrilaterals. Sections 4 and 6 solve some trigonometric Diophantine equations to identify all concave rational $a^3b$ -quadrilaterals suitable for tiling, and then find all of their tilings. Sections 5 and 7 handle two degenerate cases when the quadrilateral becomes some triangle, and thus complete the classification.

2 Basic facts

We will always express angles in units of $\pi $ radians for simplicity. So the sum of all angles at a vertex is $2$ . We present some basic facts and techniques in this section.

Let $v,e,f$ be the numbers of vertices, edges, and tiles in a quadrilateral tiling. Let $v_k$ be the number of vertices of degree k. Euler’s formula $v-e+f=2$ implies (see [10]):

(2.1) $$ \begin{align} f&=6+ \sum_{k=4}^{\infty}(k-3)v_k =6+v_4+2v_5+3v_6+\ldots, \end{align} $$

(2.2) $$ \begin{align} v_3 &=8+\sum_{k=5}^{\infty}(k-4)v_k=8+v_5+2v_6+3v_7+\ldots. \end{align} $$

So $f\ge 6$ and $v_3 \ge 8$ .

Lemma 2.1 [10, Lem. 2]

If all tiles in a tiling of the sphere by f quadrilaterals have the same four angles $\alpha ,\beta ,\gamma ,\delta $ , then

$$\begin{align*}\alpha+\beta+\gamma+\delta = 2+\frac{4}{f} , \end{align*}$$

ranging in $(2,\frac 83]$ . In particular, no vertex contains all four angles.

Lemma 2.2 [18, Lem. 3]

If the quadrilateral in Figure 1 is simple, then $\beta <\gamma $ is equivalent to $\alpha>\delta $ .

Lemma 2.3. If the quadrilateral in Figure 1 is simple, then $\beta =\delta $ if and only if $\alpha =1$ . Furthermore, if it is convex with all angles $<1$ , then $\beta>\delta $ is equivalent to $\alpha <\gamma $ , and $\beta <\delta $ is equivalent to $\alpha>\gamma $ .

Proof. If $\alpha =1$ , we get an isosceles triangle in the first picture of Figure 8, thus $\beta =\delta $ . If $\beta =\delta $ and $\alpha \neq 1$ , then $\angle CBD = \angle BDC$ implies $\angle ABD = \angle ADB$ . So we get $a=b$ , a contradiction. When the quadrilateral is convex with all angles $<1$ , the line $AC$ in the second of Figure 8 is inside the quadrilateral, and divides $\alpha $ and $\gamma $ as $\gamma =\theta +\gamma '$ and $\alpha =\theta +\alpha '$ . Then

$$\begin{align*}\alpha<\gamma \iff \alpha'<\gamma' \iff a<b. \end{align*}$$

By the same reason, we have $\beta>\delta \iff a<b$ . Therefore, $\beta>\delta $ is equivalent to $\alpha <\gamma $ . Similarly $\beta <\delta $ is equivalent to $\alpha>\gamma $ .

Lemma 2.4. If the quadrilateral in Figure 1 is simple, and $\delta \le 1$ , then $2\alpha +\beta>1$ and $\beta +2\gamma>1$ .

Proof. If all angles are $< 1$ , then the quadrilateral is convex and the line $AC$ is inside the quadrilateral in the second picture of Figure 8. Thus $\theta <\alpha ,\gamma $ . This implies $2\alpha +\beta>2\theta +\beta >1$ and $\beta +2\gamma>\beta +2\theta >1$ .

Figure 8 Proof of Lemmas 2.3 and 2.4.

If $\beta \ge 1$ or both $\alpha ,\gamma \ge 1$ , then both inequalities certainly hold. If $\delta =1$ , then $\alpha =\gamma $ by Lemma 2.3, and $2\alpha +\beta>1$ as the angle sum of a triangle. So we only need to consider the following two cases:

1. 1. $\alpha ,\beta ,\delta < 1$ and $\gamma \ge 1$ .

2. 2. $\beta ,\gamma ,\delta < 1$ and $\alpha \ge 1$ .

Case $1$ is shown in the third picture of Figure 8, and it suffices to show $2\alpha +\beta>1$ . By $\alpha ,\delta <1$ and $AB=CD=a<1$ , both B and C lie in the interior of the same hemisphere bounded by the great circle $\bigcirc AD$ . By $\beta < 1\le \gamma $ and $\alpha>\delta $ (Lemma 2.2), the line $AC$ is inside the quadrilateral. Then $\alpha \ge \theta $ as in the second picture of Figure 8, and $2\alpha +\beta>2\theta +\beta >1$ . Case $2$ can be proved similarly.

Lemma 2.5 (Parity Lemma, [18, Lem. 10])

In an $a^3b$ -tiling, the total number of $ab$ -angles $\alpha $ and $\delta $ at any vertex is even.

Lemma 2.6 (Balance Lemma, [18, Lem. 11])

In a tiling of the sphere by f congruent tiles, each angle of the tile appears f times in total. In an $a^3b$ -tiling, if either $\alpha ^2\cdots $ or $\delta ^2\cdots $ is not a vertex, then any vertex either has no $\alpha ,\delta $ , or is of the form $\alpha \delta \cdots $ with no more $\alpha ,\delta $ in the remainder.

The very useful tool adjacent angle deduction (abbreviated as AAD) has been introduced in [17, Sec. 2.5]. We give a quick review here using Figure 9. Let “ $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ ” denote an a-edge and “ $\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}$ ” denote a b-edge. Then we indicate the arrangements of angles and edges by denoting the vertices as $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ . The notation can be reversed, such as $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ ; and it can be rotated, such as $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}=\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ . We also denote the first vertex in Figure 9 as $\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \cdots $ , $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots ,\alpha \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \cdots $ , $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\cdots $ , and denote the consecutive angle segments as $\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta $ , $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em},\alpha \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta $ , $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}$ .

Figure 9 Different adjacent angle deductions of $\alpha ^2\beta ^2$ .

The pictures of Figure 9 have the same vertex $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ , but different arrangements of the four tiles. To indicate the difference, we write ${}^{\lambda }\theta ^{\mu }$ to mean $\lambda ,\mu $ are the two angles adjacent to $\theta $ in the quadrilateral. The first picture has the AAD $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha ^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\delta }\alpha ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\alpha }\beta ^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta ^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ . The second and third have the AAD $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha ^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\delta }\alpha ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta ^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\alpha }\beta ^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ and $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha ^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\delta }\alpha ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\alpha }\beta ^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\alpha }\beta ^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ , respectively. The following useful lemma is from [17, Lem. 10].

Lemma 2.7. Suppose $\lambda $ and $\mu $ are the two angles adjacent to $\theta $ in a quadrilateral.

• • If $\lambda \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\lambda \cdots $ is not a vertex, then $\theta ^n$ has the unique AAD $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\lambda }\theta ^{\mu }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\lambda }\theta ^{\mu }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\lambda }\theta ^{\mu }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ .

• • If n is odd, then we have the AAD $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\lambda }\theta ^{\mu }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\lambda }\theta ^{\mu }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ at $\theta ^n$ .

Lemma 2.8. There is no tiling of the sphere by congruent quadrilaterals with two angles $\ge 1$ .

Proof. If any two angles, say $\alpha ,\beta $ , are greater than or equal to $1$ , then $\alpha \cdots =\alpha \gamma ^x\delta ^y(x+y\ge 2)$ , $\beta \cdots =\beta \gamma ^p\delta ^q(p+q\ge 2)$ . Given that $\#\alpha =\#\beta =f$ , we deduce that $\#\gamma +\#\delta \ge 4f$ , which contradicts $\#\gamma +\#\delta =2f$ .

Proposition 2.9. There is no tiling of the sphere by congruent symmetric $a^3b$ -quadrilaterals ( $\alpha =\delta $ and $\beta =\gamma $ ).

Proof. The convex case with all angles $<1$ has been proved by Akama and van Cleemput in [1]. If any angle is $\ge 1$ , we get two angles $\ge 1$ by symmetry, then Lemma 2.8 applies.

Lemma 2.10. Assume $\gamma ^{\frac {f}{2}}$ is a vertex in an $a^3b$ -tiling. If $\beta ^2\cdots $ or $\delta ^2\cdots $ is not a vertex, and $\beta \delta \cdots =\alpha \beta \delta $ , then the tiling must be a two-layer earth map tiling $T(f\alpha \beta \delta ,2\gamma ^{\frac {f}{2}})$ in Figure 10. In particular, if all $\beta $ -vertices are $\alpha \beta \delta $ , then the tiling must be a two-layer earth map tiling.

Proof. By Lemma 2.7, when $\beta ^2\cdots $ or $\delta ^2\cdots $ is not a vertex, we have the unique AAD $\gamma ^{\frac {f}{2}}=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma ^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma ^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ . In Figure 10, $\gamma _1\gamma _2\gamma _3\cdots $ determines $T_1,T_2,T_3$ . Then $\beta _2\delta _1\cdots =\alpha _4\beta _2\delta _1$ determines $T_4$ ; $\beta _3\delta _2\cdots =\alpha _5\beta _3\delta _2,\alpha _2\beta _4\delta _5\cdots =\alpha _2\beta _4\delta _5$ determines $T_5$ . The argument started at $\alpha _4\beta _2\delta _1$ can be repeated at $\alpha _5\beta _3\delta _2$ . More repetitions give the unique tiling of f tiles with $2\gamma ^{\frac {f}{2}}$ and $f\alpha \beta \delta $ .

Lemma 2.11. In an $a^3b$ -tiling, if $\alpha \ge 1$ , then either $\alpha \beta \delta $ or $\alpha \gamma \delta $ is a vertex, and the only other possible vertex with $\alpha $ or $\delta $ must be $\alpha \gamma ^l\delta $ or $\alpha \beta ^l\delta $ , respectively, for some $l\ge 2$ .

Figure 10 A two-layer earth map tiling $T(f\alpha \beta \delta ,2\gamma ^{\frac {f}{2}})$ .

Proof. $\alpha \ge 1$ implies $\alpha ^2\cdots $ is not a vertex. Then Balance Lemma 2.6 and Lemma 2.1 imply that any vertex with $\alpha $ or $\delta $ must be of two types $\alpha \beta ^l\delta $ or $\alpha \gamma ^m\delta $ . If there exists only one type, say $\alpha \beta ^l\delta $ , then $l=1$ by Balance Lemma 2.6. If there exist both types with $l,m\ge 2$ , then the only solution satisfying Balance Lemma 2.6 is: $\{\frac f2 \alpha \beta ^2\delta ,\frac f2 \alpha \gamma ^2\delta \}$ . This implies $\beta =\gamma $ , contradicting Proposition 2.9. Therefore, one of $l,m$ must be $1$ , and the other must be $\ge 2$ since $\beta \neq \gamma $ .

Lemma 2.12. In an $a^3b$ -tiling, the a-edge and two diagonals are always $<1$ . If both $\beta ,\gamma <1$ , then $b<1$ .

Proof. By Lemma 2.8, there are just three types of simple quadrilaterals suitable for tiling: convex with all angles $<1$ , $\alpha \ge 1$ , or $\beta \ge 1$ , as shown in Figure 11. It is clear that $a<1$ , otherwise $BC$ and $CD$ would intersect at the antipodal of C, contradicting the simpleness.

Figure 11 Proof of Lemmas 2.12 and 2.13.

For the first two types in Figure 11, both $\beta <1$ and $\gamma <1$ , then $a<1$ implies that both A and D lie in the interior of the same hemisphere bounded by the great circle $\bigcirc BC$ . Therefore, two diagonals and b-edge are all $<1$ .

For the last type in Figure 11, both $\alpha <1$ and $\delta <1$ , then $a<1$ implies that both B and C lie in the interior of the same hemisphere bounded by the great circle $\bigcirc AD$ . Therefore, both diagonals are $<1$ .

Lemma 2.13. For $a^3b$ -quadrilaterals, the following equations (2.3) and (2.4) always hold, and one of the equations (2.5) or (2.6) must hold.

(2.3) $$ \begin{align} \begin{aligned} \cos b=& \cos^3 a(1-\cos \beta)(1-\cos \gamma)-\cos^2 a\sin \beta\sin \gamma+\\ &\cos a(\cos \beta+\cos \gamma-\cos \beta\cos \gamma) +\sin\beta\sin\gamma; \end{aligned} \end{align} $$

(2.4) $$ \begin{align} \cos a=\frac{\sin \alpha+\cos\delta\sin\gamma}{2\sin\delta\sin^2\frac{\gamma}{2}}=\frac{\sin \delta+\cos\alpha\sin\beta}{2\sin\alpha\sin^2\frac{\beta}{2}} \quad (\alpha,\delta\neq1); \end{align} $$

(2.5) $$ \begin{align} \sin(\alpha-\frac{\gamma}{2})\sin\frac{\beta}{2}=\sin\frac{\gamma}{2}\sin(\delta-\frac{\beta}{2}), \end{align} $$

(2.6) $$ \begin{align} \text{or}\,\,\, \sin(\alpha+\frac{\gamma}{2})\sin\frac{\beta}{2}=-\sin\frac{\gamma}{2}\sin(\delta+\frac{\beta}{2}). \end{align} $$

Proof. The equation (2.3) always holds by the extended cosine law in [17, Lem. 11]. By Lemma 2.8, there are just three types of simple quadrilaterals suitable for tiling: convex with all angles $<1$ , $\alpha \ge 1$ , or $\beta \ge 1$ , as shown in Figure 11.

For the first type, Lemma 2.12 implies that all edges and diagonals are $<1$ . Therefore, all Coolsaet’s assumptions in [4, Th. 2.1] hold and the equation (2.4) was proved there, which further implies either the equation (2.5) or (2.6).

It turns out Coolsaet’s proof works for the other two types too. If $\alpha \ge 1$ , the sine law $\frac {\sin (2-\alpha )}{\sin y}=\frac {\sin (\psi -\delta )}{\sin a}$ is equivalent to $\frac {\sin \alpha }{\sin y}=\frac {\sin (\delta -\psi )}{\sin a}$ . If $\beta \ge 1$ , the sine law $\frac {\sin (2-\beta )}{\sin x}=\frac {\sin (\phi )}{\sin a}$ is equivalent to $\frac {\sin \beta }{\sin x}=\frac {\sin (-\phi )}{\sin a}$ . Then every step to derive the equation (2.4) is exactly the same as the first type, which further implies either the equation (2.5) or (2.6).

We remark that Coolsaet also showed the equation (2.6) never holds for the first type, but it seems difficult to dismiss (2.6) for the two concave types. It is amazing that all rational solutions (rational multiples of $\pi $ ) to (2.5) or (2.6) can be found via the algebra of cyclotomic fields in Conway–Jones [3], as Coolsaet [4] did for convex $a^3b$ -quadrilaterals using Myerson’s Theorem [12] for (2.5). We summarize the algorithm as the following easy-to-use proposition.

Proposition 2.14. All solutions of $\sin x_1 \sin x_2=\sin x_3 \sin x_4$ with rational angles $0\le x_1,x_2,x_3,x_4\le \frac 12$ fall into the following four cases:

• Case 1. $x_1 x_2=x_3 x_4=0$ .

• Case 2. $\{x_1, x_2\}=\{ x_3, x_4\}$ .

• Case 3. $\{x_1, x_2\}=\{ \frac {1}{6},\theta \}$ and $\{x_3,x_4\}=\{\frac {\theta }{2},\frac {1}{2}-\frac {\theta }{2}\}$ , or $\{x_3,x_4\}=\{\frac {1}{6},\theta \}$ and $\{x_1,x_2\}=\{\frac {\theta }{2},\frac {1}{2}-\frac {\theta }{2}\}$ , for some $0<\theta \le \frac {1}{2}$ .

• Case 4. Up to reordering, all other solutions $x_1,x_2,x_3,x_4$ satisfying $0<x_1<x_3\le x_4<x_2\le \frac 12$ are in Table 3.

Table 3 Nongeneric solutions in Proposition 2.14

Remark 2.15. We always have $\sin \frac 16 \, \sin \theta =\sin \frac {\theta }{2} \, \sin (\frac 12-\frac {\theta }{2})$ . But it is a lengthy computation to get Case $3$ when we transform all angles in this formula to the range $(0,1/2]$ for all possible ranges of $\theta $ . We omit the details here.

Remark 2.16. After Case $1,$ we can assume all $x_i>0$ . Case $2$ and Case $3$ have a common solution $\{ x_1, x_2\}=\{ x_3, x_4\}=\{\frac 16,\frac 13\}$ .

Remark 2.17. The $7/15$ highlighted in a box in Table 3 was $8/15$ in Myerson’s original table, which is an obvious typo since $8/15> 1/2$ . This typo remained in [4] but the results there were nonetheless correct.

We will use lemma/proposition $n'$ to denote the use of lemma/proposition n after interchanging $\alpha \leftrightarrow \delta $ and $\beta \leftrightarrow \gamma $ .

By Lemma 2.8, the quadrilateral in our tiling can have at most one angle $\ge 1$ . Up to the symmetry of interchanging $\alpha \leftrightarrow \delta $ and $\beta \leftrightarrow \gamma $ , we need only to consider five possibilities: convex (all angles $<1$ ), concave ( $\alpha>1$ or $\beta>1$ ), or degenerate ( $\alpha =1$ or $\beta =1$ ), which will be discussed in the following sections, respectively.

3 Convex case $\alpha ,\beta ,\gamma ,\delta <1$

Coolsaet [4, Th. 3.2] classified simple convex rational quadrilateral with three equal sides into $29$ sporadic examples in the first column of Table 4 and $7$ infinite classes (up to interchanging $\alpha \leftrightarrow \delta $ and $\beta \leftrightarrow \gamma $ ):

1. 1. $\alpha =\gamma $ and $\beta =\delta $ (and all four sides are equal);

2. 2. $\alpha =\delta $ and $\beta =\gamma $ ;

3. 3. $\alpha =\frac {\gamma }{2}$ and $\delta =\frac {\beta }{2}$ , $\alpha ,\delta <\frac {1}{2}$ ;

4. 4. $\alpha =\frac {3\gamma }{2},\beta =\frac {1}{3}$ and $\delta =\frac {2}{3}-\frac {\gamma }{2}$ , with $\frac {1}{2}<\gamma <\frac {2}{3}$ ;

5. 5. $\alpha =\frac {1}{6}+\frac {\gamma }{2},\beta =2\gamma $ and $\delta =\frac {1}{2}+\frac {\gamma }{2}$ , with $\frac {1}{3}<\gamma <\frac {1}{2}$ ;

6. 6. $\alpha =\frac {1}{6}+\frac {\gamma }{2},\beta =2\gamma $ and $\delta =\frac {1}{2}+\frac {3\gamma }{2}=3\alpha $ , with $\frac {4}{15}<\gamma <\frac {1}{3}$ ;

7. 7. $\alpha =\frac {1}{6}+\frac {\gamma }{2},\beta =2-2\gamma $ and $\delta =\frac {3}{2}-\frac {3\gamma }{2}$ , with $\frac {1}{2}<\gamma <\frac {5}{6}$ .

In fact, Coolsaet assumed additionally that all edges and diagonals are $<1$ , and our Lemma 2.12 shows that such assumptions are satisfied automatically for $a^3b$ -tilings. Cases $1$ and $2$ are immediately dismissed due to $a\neq b$ and Proposition 2.9. In this section, we will find all possible tilings from Table 4 and from five remaining cases.

Table 4 All $29$ sporadic convex rational $a^3b$ -quadrilaterals

3.1 Sporadic cases in Table 4

A quadrilateral is qualified to tile the sphere only if its angle sum is $2+\frac {4}{f}$ for some even integer $f\ge 6$ , every angle can be extended to a vertex, and there must also exist degree $3$ vertices by the equation (2.2). These basic criteria dismiss most sporadic examples in Table 4, as the details showing in the second and third columns. There are only three subcases left. But $(21,8,26,7)/30$ implies $\alpha \cdots =\alpha \beta ^4\delta $ and $(17,16,26,11)/30$ implies $\gamma \cdots =\alpha ^2\gamma $ , both contradicting Balance Lemma 2.6. So only $(23,10,28,9)/30$ admits a two-layer earth map tiling $T(12\alpha \gamma \delta ,2\beta ^6)$ . In fact the only other possible vertex is $\alpha \beta \delta ^3$ , but Lemma 2.10 ^′ shows that there is no other tilings. This is $f=12$ , $(9, 28, 10, 23)/30$ in Table 1 after interchanging $\alpha \leftrightarrow \delta $ and $\beta \leftrightarrow \gamma $ .

3.2 Case 3. $\alpha =\frac {\gamma }{2},\delta =\frac {\beta }{2}$ , $\alpha ,\delta <\frac {1}{2}$

By Lemma 2.1, we get $\frac {2}{3}<\alpha +\delta \le \frac {8}{9}$ and $\frac {4}{3}<\beta +\gamma \le \frac {16}{9}$ . Without loss of generality, let $\beta>\gamma $ . So we get $\beta>\frac {2}{3}$ , and $\delta>\frac {1}{3}$ by Lemma 2.3. By $\beta <1$ , we get $\gamma>\frac {1}{3},\alpha >\frac {1}{6}$ , and $\delta <\frac {1}{2}$ . Let $R(\beta ^2\cdots )$ denote the remainder or “ $\cdots $ ” part of the angles at this vertex $\beta ^2\cdots $ . By $R(\beta ^2\cdots )<\beta =2\delta ,\gamma =2\alpha $ and Parity Lemma, there is no $\beta ^2\cdots $ vertex. Similarly, there is no $\beta \delta ^2\cdots $ vertex. By $\alpha <R(\beta \delta \cdots )<3\alpha $ and Parity Lemma, there is no $\beta \delta \cdots $ vertex. By $R(\beta \cdots )<3\gamma $ , $\gamma =2\alpha $ and Parity Lemma, we get $\beta \cdots =\beta \gamma ^2,\alpha ^2\beta \gamma $ or $\alpha ^4\beta $ . They all satisfy $\#\alpha +\#\gamma \ge 2\#\beta $ . If $\alpha ^2\beta \gamma $ or $\alpha ^4\beta $ is a vertex, then $\#\alpha +\#\gamma>2\#\beta $ , contradicting Balance Lemma 2.6. If $\beta \cdots =\beta \gamma ^2$ , then $\#\gamma>\#\beta $ , again a contradiction. We conclude that there is no tiling in this case.

3.3 Case 4. $\alpha =\frac {3\gamma }{2},\beta =\frac {1}{3},\delta =\frac {2}{3}-\frac {\gamma }{2},\frac {1}{2}<\gamma <\frac {2}{3}$

We have $\frac {3}{4}<\alpha <1$ and $\frac {1}{3}<\delta <\frac {5}{12}$ . By $R(\gamma \cdots )<2\alpha $ , $0<R(\alpha \gamma \delta \cdots )<\beta ,\gamma ,2\delta $ and Parity Lemma, there is no $\alpha \gamma \cdots $ vertex. By $0<R(\gamma ^3\cdots )<2\beta ,\gamma ,2\delta $ and Parity Lemma, we get $\gamma ^3\cdots =\beta \gamma ^3$ . By $2\beta <R(\gamma ^2\cdots )<3\beta ,3\delta $ , $0<R(\gamma ^2\delta ^2\cdots )<\beta $ and Parity Lemma, we get $\gamma ^2\cdots =\beta \gamma ^3$ . By $ R(\gamma \delta ^2\cdots )=2\beta <2\delta , \, 4\beta <R(\gamma \cdots )<5\beta $ and Parity Lemma, we get $\gamma \cdots =\beta \gamma ^3$ or $\beta ^2\gamma \delta ^2$ . By Balance Lemma, $\beta \gamma ^3$ is a vertex. Therefore, $\alpha =\frac {5}{6},\beta =\frac {1}{3},\gamma =\frac {5}{9}$ and $\delta =\frac {7}{18}$ . Then we get $f=36$ . By Parity Lemma, we get the ${\textit {AVC}}\subset \{\alpha ^2\beta ,\alpha \delta ^3,\beta \gamma ^3,\beta ^2\gamma \delta ^2,\beta ^6\}$ .

If $\beta ^6$ is a vertex, we have the AAD $\beta ^6=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta ^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\alpha }\beta ^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ or $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta ^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta ^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ . This gives a vertex $\alpha \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha \cdots $ or $\alpha \gamma \cdots $ , contradicting the AVC. Then there is only one solution satisfying Balance Lemma 2.6: $\{14\alpha ^2\beta ,8\alpha \delta ^3,10\beta \gamma ^3,6\beta ^2\gamma \delta ^2\}$ .

In Figure 12, we have the unique AAD $\beta ^2\gamma \delta ^2=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\delta _1^{\alpha }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\alpha }\delta _2^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta _3^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma _4^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\alpha }\beta _5^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ which determines $T_1,T_2,T_3,T_4,T_5$ . Then $\alpha _5\beta _4\cdots =\alpha ^2\beta $ determines $T_6$ ; $\alpha _4\beta _6\cdots =\alpha ^2\beta $ determines $T_7$ ; $\alpha _1\delta _4\delta _7\cdots =\alpha \delta ^3$ determines $T_8$ ; $\alpha _8\delta _3\cdots =\alpha \delta ^3$ determines $T_9,T_{10}$ . We have $\gamma _2\gamma _3\gamma _{10}\cdots =\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _3\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _{10}\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta _{11}^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ or $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _3\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _{10}\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\alpha }\beta _{11}^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ . We might as well take $\gamma _2\gamma _3\gamma _{10}\cdots =\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _3\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _{10}\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta _{11}^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ which determines $T_{11}$ . Similarly, we can determine $T_{12},T_{13},T_{14},T_{15},T_{16},T_{17}$ and $T_{18}$ . We have $\beta _{10}\gamma _{11}\gamma _{13}\cdots =\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _{11}\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _{10}\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _{13}\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma _{19}^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ or $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _{11}\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _{10}\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _{13}\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma _{19}^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ . We might as well take $\beta _{10}\gamma _{11}\gamma _{13}\cdots =\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _{11}\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _{10}\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _{13}\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma _{19}^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ which determines $T_{19}$ . Similarly, we can determine $T_{20},T_{21}$ , $\dots ,T_{36}$ . For other choices of $\gamma _2\gamma _3\gamma _{10}\cdots $ and $\beta _{10}\gamma _{11}\gamma _{13}\cdots $ , we still get this tiling or its equivalent opposite. This is Case $(15, 6, 10, 7)/18$ in Table 1.

Figure 12 $T(14\alpha ^2\beta ,8\alpha \delta ^3,10\beta \gamma ^3,6\beta ^2\gamma \delta ^2)$ .

3.4 Case 5. $\alpha =\frac {1}{6}+\frac {\gamma }{2},\beta =2\gamma ,\delta =\frac {1}{2}+\frac {\gamma }{2},\frac {1}{3}<\gamma <\frac {1}{2}$

We have $\frac {1}{3}<\alpha <\gamma <\frac {1}{2}$ and $\frac {2}{3}<\delta <\beta <1$ . By $R(\beta ^2\cdots )<2\alpha ,\beta ,2\gamma ,\delta $ and Parity Lemma, we get $\beta ^2\cdots =\beta ^2\gamma $ . By $R(\alpha \beta \delta \cdots )< \text {all angles}$ , $0<R(\alpha ^2\beta \cdots )<2\alpha ,2\gamma $ , $2\gamma <R(\beta \cdots )<4\gamma ,2\delta $ and Parity Lemma, we get $\beta \cdots =\alpha \beta \delta ,\beta ^2\gamma ,\alpha ^2\beta \gamma $ or $\beta \gamma ^3$ . However, $\alpha \beta \delta ,\beta ^2\gamma $ or $\beta \gamma ^3$ implies $f=9$ or $15$ , contradicting the fact that f is even. So we have only $\beta \cdots =\alpha ^2\beta \gamma $ with $f=12$ . But this again contradicts Balance Lemma 2.6. We conclude that there is no tiling in this case.

3.5 Case 6. $\alpha =\frac {1}{6}+\frac {\gamma }{2},\beta =2\gamma ,\delta =\frac {1}{2}+\frac {3\gamma }{2}=3\alpha ,\frac {4}{15}<\gamma <\frac {1}{3}$

We have $\frac {3}{10}<\alpha <\frac {1}{3},\frac {8}{15}<\beta <\frac {2}{3}$ and $\frac {9}{10}<\delta <1$ . By $R(\delta ^2\cdots )< \text {all angles}$ , there is no $\delta ^2\cdots $ vertex. By $0<R(\alpha ^3\delta \cdots )<\text {all angles}$ , $0<R(\alpha \beta \delta \cdots )< \text {all angles}$ , $2\gamma <R(\alpha \delta \cdots )<3\gamma $ and Parity Lemma, there is no $\delta \cdots $ vertex, a contradiction. We conclude that there is no tiling in this case.

3.6 Case 7. $\alpha =\frac {1}{6}+\frac {\gamma }{2},\beta =2-2\gamma ,\delta =\frac {3}{2}-\frac {3\gamma }{2},\frac {1}{2}<\gamma <\frac {5}{6}$

By Lemma 2.1, we have $\alpha =\frac {7}{12}-\frac {1}{f},\beta =\frac {1}{3}+\frac {4}{f},\gamma =\frac {5}{6}-\frac {2}{f}$ and $\delta =\frac {1}{4}+\frac {3}{f}$ . So we have $\frac {5}{12}<\alpha <\gamma <\frac {5}{6}$ and $\frac {1}{4}<\delta <\beta <1$ .

If $\beta>\gamma $ , then we get $6<f<12$ . So we have $\frac {5}{12}<\alpha <\frac 12<\delta <\frac {3}{4}$ and $\frac {1}{2}<\gamma <\frac {2}{3}<\beta <1$ . By $R(\beta ^2\cdots )<2\alpha ,\beta ,\gamma ,2\delta $ and Parity Lemma, there is no $\beta ^2\cdots $ vertex. By $0<R(\alpha ^2\beta \cdots )<\text {all angles}$ , $R(\alpha \beta \delta \cdots )<\text {all angles}$ , $R(\beta \delta ^2\cdots )<\text {all angles}$ , $R(\beta \cdots )=2\gamma $ and Parity Lemma, we get $\beta \cdots =\alpha \beta \delta ,\beta \gamma ^2$ or $\beta \delta ^2$ . Suppose $\alpha \beta \delta $ or $\beta \delta ^2$ is a vertex. Then we get $f=\frac {36}{5}$ or $\frac {60}{7}$ , a contradiction. So we have $\beta \cdots =\beta \gamma ^2$ . But this again contradicts Balance Lemma 2.6.

Therefore, $\beta <\gamma $ , then we get $f>12$ . So we have $\frac {1}{4}<\delta <\frac 12<\alpha <\frac {7}{12}$ and $\frac {1}{3}<\beta <\frac {2}{3}<\gamma <\frac 56$ .

If $\alpha ^k\beta ^l\gamma ^m\delta ^n$ is a vertex, then we have

$$\begin{align*}(\tfrac{7}{12}-\tfrac{1}{f})k+(\tfrac13+\tfrac{4}{f})l+(\tfrac{5}{6}-\tfrac{2}{f})m+(\tfrac{1}{4}+\tfrac{3}{f})n=2. \end{align*}$$

We also have $\alpha> \frac {1}{2},\beta >\frac {1}{3},\gamma >\frac {2}{3},\delta >\frac {1}{4}$ . This implies $k \le 3,l\le 5,m \le 2,n\le 7$ . We substitute the finitely many combinations of exponents satisfying the bounds into the equation above and solve for f. By the angle values and Parity Lemma, we get all possible AVC in Table 5. Its first row “ $f=\text {all}$ ” means that the angle combinations can be vertices for any f; all other rows are mutually exclusive. Note that the ${\textit {AVC}}\subset \{\beta \gamma ^2,\alpha ^3\delta \}$ in the first row admits no solution satisfying Balance Lemma 2.6. All possible tilings based on the other subcases are deduced as follows.

Table 5 The AVC for $\alpha =\frac {7}{12}-\frac {1}{f},\beta =\frac {1}{3}+\frac {4}{f},\gamma =\frac {5}{6}-\frac {2}{f}, \delta =\frac {1}{4}+\frac {3}{f}$

3.6.1 Table 5, $f=20,132$

For $f=20$ , the ${\textit {AVC}}\subset \{\beta \gamma ^2,\alpha ^3\delta , \alpha \beta ^2\delta \}$ admits no solution satisfying Balance Lemma 2.6.

For $f=132$ , there is no $\alpha \gamma \cdots $ vertex. Then $\beta \delta ^6$ cannot be a vertex, since its AAD gives $\alpha \gamma \cdots $ . So we get the ${\textit {AVC}}\subset \{\beta \gamma ^2,\alpha ^3\delta , \beta ^4\delta ^2 \}$ , which admits no solution satisfying Balance Lemma 2.6.

3.6.2 Table 5, $f=24$

By Table 5, there is no $\alpha \gamma \cdots $ vertex. Then $\beta \delta ^4$ cannot be a vertex, since its AAD gives $\alpha \gamma \cdots $ . So we get the ${\textit {AVC}}\subset \{\beta \gamma ^2,\alpha ^3\delta ,\beta ^4,\beta \gamma \delta ^2 \}$ , which admits a unique solution satisfying Balance Lemma 2.6: $\{8\beta \gamma ^2,8\alpha ^3\delta ,2\beta ^4,8\beta \gamma \delta ^2\}$ .

In Figure 13, by the AVC, we know $\alpha \gamma \cdots $ is not a vertex. So we have the AAD $\beta ^4=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\alpha }\beta _1^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta _2^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\alpha }\beta _3^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta _4^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ . This determines $T_1,T_2,T_3,T_4$ . Then $\gamma _1\gamma _2\cdots =\beta _5\gamma _1\gamma _2$ determines $T_5$ . Then $\alpha _5\delta _2\cdots =\alpha _5\alpha _6\alpha _7\delta _2$ determines $T_6,T_7$ . Then $\gamma _5\delta _1\cdots =\beta _9\gamma _5\delta _1\delta _8$ determines $T_8$ . By $\beta _9$ , we have $\alpha _9\gamma _8\cdots $ or $\alpha _9\delta _5\delta _6\cdots $ , contradicting the AVC.

Figure 13 $f=24$ , the ${\textit {AVC}}=\{\beta \gamma ^2,\alpha ^3\delta ,\beta ^4,\beta \gamma \delta ^2\}$ admit no tiling.

3.6.3 Table 5, $f=60$

By Table 5, there is no $\alpha \gamma \cdots $ vertex. Then $\beta ^5$ cannot be a vertex, since its AAD gives $\alpha \gamma \cdots $ . So we get the ${\textit {AVC}}\subset \{\beta \gamma ^2,\alpha ^3\delta ,\beta ^3\gamma ,\gamma \delta ^4,\beta ^2\delta ^4 \}$ . By Lemma 2.7, the AAD of $\beta ^2\delta ^4$ must be $\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\alpha }\delta ^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\delta ^{\alpha }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\cdots $ . This gives a vertex $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma ^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ . By the AVC, we have $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma ^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots =\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma ^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\alpha }\beta ^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ . This gives a vertex $\alpha \beta \cdots $ , contradicting the AVC. Therefore, $\beta ^2\delta ^4$ is not a vertex. Similarly, $\gamma \delta ^4$ is not a vertex. Then $\delta \cdots =\alpha ^3\delta $ , contradicting Balance Lemma 2.6.

3.6.4 Table 5, $f=84$

By Table 5, we get the ${\textit {AVC}}\subset \{\beta \gamma ^2,\alpha ^3\delta ,\alpha \beta ^3\delta ,\alpha \delta ^5 \}$ , which admits a unique solution satisfying Balance Lemma 2.6: $\{42\beta \gamma ^2,20\alpha ^3\delta ,14\alpha \beta ^3\delta ,10\alpha \delta ^5\}$ . Since $\alpha \gamma \cdots $ is not a vertex, we have the AAD $\alpha \beta ^3\delta =\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha ^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\alpha }\delta ^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta ^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\alpha }\beta ^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta ^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ . This gives a vertex $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma ^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ . By the AVC, we have $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma ^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots =\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma ^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta ^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ . This gives a vertex $\gamma \delta \cdots $ , contradicting the AVC.

3.6.5 Table 5, $f=36$

By Table 5, there is no $\alpha \gamma \cdots $ vertex. Then $\beta ^3\delta ^2$ cannot be a vertex, since its AAD gives $\alpha \gamma \cdots $ . So we get the ${\textit {AVC}}\subset \{\beta \gamma ^2,\alpha ^3\delta ,\alpha ^2\beta ^2,\alpha \beta \delta ^3,\delta ^6 \}$ , and $\alpha =\frac 59,\beta =\frac {4}{9},\gamma =\frac 79,\delta =\frac 13$ . If $\delta ^6$ is not a vertex, there is only one solution satisfying Balance Lemma 2.6: $\{18\beta \gamma ^2,6\alpha ^3\delta ,4\alpha ^2\beta ^2,10\alpha \beta \delta ^3\}$ .

In Figure 14, we have the unique AAD $\alpha ^3\delta =\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\alpha _1\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha _2\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\alpha _3\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\delta _4\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}$ which determines $T_1,T_2,T_3,T_4$ . Then $\beta _3\gamma _4\cdots =\beta _3\gamma _4\gamma _5$ . By $\gamma _5$ , $\gamma _3\cdots =\beta _5\gamma _3\cdots $ determines $T_5$ . Then $\beta _1\beta _2\cdots =\alpha _6\alpha _7\beta _1\beta _2$ determines $T_6,T_7$ ; $\beta _7\gamma _1\cdots =\beta _7\gamma _1\gamma _8$ . By $\gamma _8$ , $\gamma _7\cdots =\beta _8\gamma _7\cdots $ determines $T_8$ . Then $\alpha _4\delta _1\delta _8\cdots =\alpha _4\beta _{10}\delta _1\delta _8\delta _9$ determines $T_9$ . By $\beta _{10}$ , $\gamma _9\cdots =\beta _{11}\gamma _9\gamma _{10}$ determines $T_{10}$ . By $\beta _{11}$ , $\delta _{10}\cdots =\alpha _{11}\delta _{10}\cdots $ determines $T_{11}$ . Then $\alpha _{10}\beta _4\delta _5\cdots =\alpha _{10}\beta _4\delta _5\delta _{12}\delta _{13}$ determines $T_{12},T_{13}$ ; $\alpha _{11}\alpha _{13}\delta _{10}\cdots =\alpha _{11}\alpha _{13}\alpha _{14}\delta _{10}$ determines $T_{14}$ ; $\beta _6\gamma _2\cdots =\beta _6\gamma _2\gamma _{15}$ . By $\gamma _{15}$ , $\gamma _6\cdots =\beta _{15}\gamma _6\cdots $ determines $T_{15}$ . Then $\delta _2\delta _3\delta _{15}\cdots =\alpha _{16}\beta _{17}\delta _2\delta _3\delta _{15}$ determines $T_{16}$ ; $\beta _5\gamma _3\cdots =\beta _5\gamma _3\gamma _{17}$ determines $T_{17}$ ; $\alpha _5\alpha _{12}\delta _{17}\cdots =\alpha _5\alpha _{12}\alpha _{18}\delta _{17}$ determines $T_{18}$ ; $\beta _{12}\beta _{18}\cdots =\alpha _{19}\alpha _{20}\beta _{12}\beta _{18}$ determines $T_{19}$ ; $\beta _{20}\gamma _{12}\gamma _{13}\cdots =\beta _{20}\gamma _{12}\gamma _{13}$ determines $T_{20}$ . Then we get $\beta _{13}\beta _{14}\gamma _{20}\cdots $ , contradicting the AVC.

Figure 14 $f=36$ , the ${\textit {AVC}}=\{\beta \gamma ^2, \alpha ^3\delta ,\alpha ^2\beta ^2,\alpha \beta \delta ^3\}$ admit no tiling.

Therefore, $\delta ^6$ is a vertex. We have the unique AAD for $\delta ^6=\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\delta _1\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\delta _2\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\cdots $ which determines $T_1,T_2,T_3,T_4,T_5,T_6$ . Then $\gamma _1\gamma _2\cdots =\beta _7\gamma _1\gamma _2$ determines $T_7$ . So $\alpha _2\alpha _3\cdots =\alpha ^2\beta ^2$ or $\alpha ^3\delta $ , shown in Figures 15 and 16, respectively.

Figure 15 Case $\alpha _2\alpha _3\cdots =\alpha ^2\beta ^2$ admits no tiling.

Figure 16 Case $\alpha _2\alpha _3\cdots =\alpha ^3\delta $ admits $T(18\beta \gamma ^2,6\alpha ^3\delta ,6\alpha ^2\beta ^2,6\alpha \beta \delta ^3,2\delta ^6)$ .

In Figure 15, $\alpha _2\alpha _3\cdots =\alpha _2\alpha _3\beta _8\beta _9$ . Then $\beta _2\gamma _7\cdots =\beta _2\gamma _7\gamma _8$ determines $T_8$ . By $\beta _9$ , $\alpha _8\cdots =\alpha _8\alpha _9\cdots $ determines $T_9$ . Then $\gamma _3\gamma _4\cdots =\beta _{10}\gamma _3\gamma _4,\beta _3\gamma _9\cdots =\beta _3\gamma _9\gamma _{10}$ determine $T_{10}$ ; $\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\alpha _8\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha _9\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\cdots =\alpha _8\alpha _9\alpha _{12}\delta _{11}$ determines $T_{11},T_{12}$ ; $\beta _{12}\gamma _{11}\cdots \ =\beta _{12}\gamma _{11}\gamma _{13}$ . By $\gamma _{13}$ , $\gamma _{12}\cdots =\beta _{13}\gamma _{12}\cdots $ determines $T_{13}$ . We have $\alpha _{10}\beta _4\cdots =\alpha ^2\beta ^2$ or $\alpha \beta \delta ^3$ . If $\alpha _{10}\beta _4\cdots =\alpha \beta \delta ^3$ , then we get $\alpha _4\alpha _5\gamma \cdots $ , contradicting the AVC. Therefore, $\alpha _{10}\beta _4\cdots =\alpha _{10}\alpha _{14}\beta _4\beta _{15}$ . This determines $T_{14}$ . By $\beta _{15}$ , $\alpha _4\alpha _5\cdots =\alpha _4\alpha _5\alpha _{15}\delta _{16}$ determines $T_{15},T_{16}$ ; $\delta _9\delta _{10}\delta _{12}\delta _{14}\cdots =\delta _9\delta _{10}\delta _{12}\delta _{14}\delta _{17}\delta _{18}$ determines $T_{17},T_{18}$ ; $\beta _{14}\gamma _{15}\cdots =\beta _{14}\gamma _{15}\gamma _{19}$ , $\gamma _{14}\gamma _{18}\cdots =\beta _{19}\gamma _{14}\gamma _{18}$ determine $T_{19}$ ; $\alpha _{16}\delta _{15}\delta _{19}\cdots = \alpha _{16}\delta _{15}\delta _{19}\delta _{20}\cdots $ determines $T_{20}$ ; $\alpha _{19}\alpha _{20}\beta _{18}\cdots = \alpha _{19}\alpha _{20}\beta _{18}\beta _{21}$ . By $\beta _{21}$ , $\alpha _{17}\alpha _{18}\cdots =\alpha _{17}\alpha _{18}\alpha _{21}\delta _{22}$ determines $T_{21},T_{22}$ . Then we get $\alpha _{13}\beta _{17}\gamma _{22}\cdots $ , contradicting the AVC.

In Figure 16, $\alpha _2\alpha _3\cdots =\alpha ^3\delta $ . We have $\beta _2\gamma _7\cdots =\beta _2\gamma _7\gamma _8$ . By $\gamma _8$ , $\alpha _2\alpha _3\cdots =\alpha _2\alpha _3\alpha _9\delta _8$ determines $T_8,T_9$ . Then $\beta _3\beta _9\cdots =\alpha _{10}\alpha _{11}\beta _3\beta _9$ determines $T_{10},T_{11}$ ; $\beta _{11}\gamma _9\cdots =\beta _{11}\gamma _9\gamma _{12}$ . By $\gamma _{12}$ , $\gamma _{11}\cdots =\beta _{12}\gamma _{11}\cdots $ determines $T_{12}$ . Then $\alpha _8\delta _9\delta _{12}\cdots =\alpha _8\beta _{14}\delta _9\delta _{12}\delta _{13}$ determines $T_{13}$ . By $\beta _{14}$ , $\gamma _{13}\cdots =\beta _{15}\gamma _{13}\gamma _{14}$ determines $T_{14}$ . By $\beta _{15}$ , $\delta _{14}\cdots =\alpha _{15}\delta _{14}\cdots $ determines $T_{15}$ . We have $\alpha _{12}\alpha _{13}\cdots =\alpha ^3\delta $ or $\alpha ^2\beta ^2$ . If $\alpha _{12}\alpha _{13}\cdots =\alpha ^3\delta $ , then we get $\beta _{13}\gamma _{15}\beta \cdots $ or $\beta _{12}\gamma _{11}\beta \cdots $ , contradicting the AVC. Therefore, $\alpha _{12}\alpha _{13}\cdots =\alpha ^2\beta ^2$ . Then $\beta _{13}\gamma _{15}\cdots =\beta _{13}\gamma _{15}\gamma _{16},\beta _{12}\gamma _{11} \cdots =\beta _{12}\gamma _{11}\gamma _{17}$ determine $T_{16},T_{17}$ . The argument started at $T_7$ can be repeated at $T_{10}$ . Two repetitions give a unique tiling $T(18\beta \gamma ^2,6\alpha ^3\delta ,6\alpha ^2\beta ^2,6\alpha \beta \delta ^3,2\delta ^6)$ . This is Case $(5, 4, 7, 3)/9$ in Table 1.

4 Concave case $\alpha>1$

An $a^3b$ -quadrilateral with $\alpha>1,\beta ,\gamma ,\delta <1$ is shown in Figure 17, where $\phi =\angle ACB=\angle BAC$ and $\psi =\angle BDC=\angle CBD$ . We first prove some basic facts. Recall that Lemma 2.4 implies $\beta +2\gamma>1$ .

Figure 17 $a^3b$ -quadrilateral with $\alpha>1,\beta ,\gamma ,\delta <1$ .

Lemma 4.1. In an $a^3b$ -tiling with $\alpha>1$ , we have $a>b$ , $\alpha>1>\gamma >\beta >\delta $ , $\gamma>\frac {1}{3}$ and $\delta <\frac 12$ .

Proof. $\alpha>1>\gamma $ implies $\angle CAD=\alpha -\phi>\gamma -\phi =\angle ACD$ . So $a>b$ . Then $\angle ABD<\angle ADB$ . By $\angle CBD=\angle BDC$ , we get $\beta>\delta $ . By Lemma 2.2, we have $\beta <\gamma $ . By Lemma 2.4, we have $\beta +2\gamma>1$ , so $\gamma>\frac 13$ .

If $\delta \ge \frac 12$ , by $\alpha>1>\gamma >\beta >\delta $ , the sum of $\alpha $ with any two angles is $>2$ and there is no $\alpha \cdots $ vertex, a contradiction.

Lemma 4.2. In an $a^3b$ -tiling with $\alpha>1$ , if $\alpha \beta \delta $ appears, then $\gamma =\frac {2}{3},\frac 12$ or $\frac 25$ .

Proof. By $\alpha +\beta +\delta =2$ , we get $\gamma =\frac {4}{f}$ with $f\ge 6$ being even. By Lemma 4.1, $\gamma>\frac {1}{3}$ . So $f<12$ . Then $f=6,8,10$ and $\gamma =\frac {2}{3},\frac 12$ or $\frac 25$ .

To find rational $a^3b$ -quadrilaterals by solving (2.5) or (2.6) via Proposition 2.14, we have to transform $\alpha -\frac {\gamma }{2},\frac \beta 2,\frac \gamma 2,\delta -\frac \beta 2,\alpha +\frac \gamma 2,-\delta -\frac \beta 2$ to the range $[0,\frac 12]$ . For (2.5), by Lemma 4.1, we have $\frac 12<\alpha -\frac {\gamma }{2}<2$ , $0<\frac {\beta }{2},\frac {\gamma }{2}<\frac 12$ , $-\frac 12<\delta -\frac {\beta }{2}<\frac 12$ . For (2.6), by Lemma 4.1, we have $0<\frac {\beta }{2},\frac {\gamma }{2}<\frac 12,0<\delta +\frac {\beta }{2}<1$ , which implies $\sin (\alpha +\frac \gamma 2)<0$ . By $1<\alpha +\frac {\gamma }{2}<\frac 52$ , we get $1<\alpha +\frac {\gamma }{2}<2$ . Thus, we have to consider the following seven choices:

(4.1) $$ \begin{align} \{ x_1, x_2, x_3, x_4\}=\begin{cases} \{1-\alpha+\frac{\gamma}{2},\frac{\beta}{2},\frac{\gamma}{2},\delta-\frac{\beta}{2}\}, \\ \{-1+\alpha-\frac{\gamma}{2},\frac{\beta}{2},\frac{\gamma}{2},-\delta+\frac{\beta}{2}\}, \\ \{2-\alpha+\frac{\gamma}{2}, \frac{\beta}{2}, \frac{\gamma}{2}, -\delta+\frac{\beta}{2}\},\\ \{-1+\alpha+\frac{\gamma}{2},\frac{\beta}{2},\frac{\gamma}{2},\delta+\frac{\beta}{2}\}, \\ \{-1+\alpha+\frac{\gamma}{2},\frac{\beta}{2},\frac{\gamma}{2},1-\delta-\frac{\beta}{2}\}, \\ \{2-\alpha-\frac{\gamma}{2},\frac{\beta}{2},\frac{\gamma}{2},\delta+\frac{\beta}{2}\}, \\ \{2-\alpha-\frac{\gamma}{2},\frac{\beta}{2},\frac{\gamma}{2},1-\delta-\frac{\beta}{2}\}. \\ \end{cases} \end{align} $$

We will match these choices with four cases of solutions in Proposition 2.14 as follows.

4.1 Case $1$ : $x_1 x_2=x_3 x_4=0$

By $-\frac 12<\delta -\frac \beta 2<\frac 12$ , $\frac 12<\alpha -\frac \gamma 2<2$ and $0<\delta +\frac \beta 2<1$ , the only solution of $x_1 x_2=x_3 x_4=0$ for (4.1) comes from $\alpha -\frac \gamma 2=1$ and $\delta -\frac \beta 2=0$ . By Lemma 2.11, we know that $\alpha \beta \delta $ or $\alpha \gamma \delta $ is a vertex.

If $\alpha \beta \delta $ is a vertex, we get three subcases by Lemma 4.2:

1. 1. $\alpha =\frac 43,\beta =\frac 49,\gamma =\frac 23,\delta =\frac 29$ (Case $(12,4,6,2)/9$ in Table 1).

2. 2. $\alpha =\frac 54,\beta =\gamma =\frac 12,\delta =\frac 14$ .

3. 3. $\alpha =\frac 65,\beta =\frac {8}{15},\gamma =\frac 25,\delta =\frac {4}{15}$ .

For the second and third subcases, we have $\beta \ge \gamma $ , contradicting $\beta <\gamma $ in Lemma 4.1. In the first subcase, we have $\alpha \cdots =\alpha \beta \delta $ or $\alpha \delta ^3$ . By $\#\alpha =\#\delta $ , we get $\alpha \cdots =\alpha \beta \delta $ . There is only one solution satisfying Balance Lemma 2.6: $\{6\alpha \beta \delta ,2\gamma ^3\}$ , and it gives a two-layer earth map tiling by Lemma 2.10.

If $\alpha \gamma \delta $ is a vertex, then we get $\alpha =\frac 43-\frac {2}{3f},\beta =\frac {4}{f},\gamma =\frac 23-\frac {4}{3f},\delta =\frac {2}{f}$ . By Lemma 4.1, $\frac 4f=\beta <\gamma =\frac 23-\frac {4}{3f}$ . This implies $f>8$ . By the angle values, Parity Lemma and Lemma 2.11, we get the

$$\begin{align*}{\textit{AVC}}\subset\{\alpha\gamma\delta,\beta\gamma^3,\alpha\beta^{\frac{f-2}{6}}\delta,\beta^{\frac{f+4}{6}}\gamma^2,\beta^{\frac{f+1}{3}}\gamma,\beta^{\frac{f}{2}}\}.\end{align*}$$

When $f=6k(k\ge 2)$ or $6k+4(k\ge 1)$ , we have the ${\textit {AVC}}\subset \{\alpha \gamma \delta ,\beta \gamma ^3,\beta ^{\frac {f}{2}}\}$ , and the only solution satisfying Balance Lemma 2.6 is $\{ f\alpha \gamma \delta ,2\beta ^{\frac {f}{2}}\}$ which gives a two-layer earth map tiling by Lemma 2.10 ^′.

When $f=6k+2 \ (k\ge 2)$ , we have $\gamma =k\beta $ , $\alpha +\delta =(2k+1)\beta $ and the

$$\begin{align*}{\textit{AVC}}\subset\{\alpha\gamma\delta,\beta\gamma^3,\alpha\beta^k\delta,\beta^{k+1}\gamma^2,\beta^{2k+1}\gamma,\beta^{\frac{f}{2}}\}.\end{align*}$$

By the AVC, we know $\alpha ^2\cdots ,\delta ^2\cdots ,$ and $\alpha \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\delta \cdots $ are not vertices. So we have the unique AAD for any $\beta ^x\gamma ^y=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma ^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta ^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma ^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta ^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ . We will discuss all possible $\beta $ -vertices in any tiling as follows.

If $\beta ^{\frac {f}{2}}$ appears, the tiling is a two-layer earth map tiling by Lemma 2.10 ^′.

If $\beta ^{2k+1}\gamma $ appears ( $\beta ^{\frac {f}{2}}$ never appears), then $R(\gamma _2\cdots )=\beta ^{2k+1}$ in the first picture of Figure 18 and this $\beta ^{2k+1}$ determines $2k+1$ time zones ( $4k+2$ or $\frac {2f+2}{3}$ tiles). Then $R(\alpha _1\delta _4\cdots )=\beta ^{k}$ and this $\beta ^{k}$ determines k time zones ( $2k$ or $\frac {f-2}{3}$ tiles). We obtain a unique tiling $T(6k\alpha \gamma \delta ,2\alpha \beta ^{k}\delta ,2\beta ^{2k+1}\gamma )$ which can be viewed as the first flip modification of the two-layer earth map tilings.

Figure 18 Tilings by flipping once, or twice with different spacing.

If $\beta ^{k+1}\gamma ^2$ appears ( $\beta ^{2k+1}\gamma ,\beta ^{\frac {f}{2}}$ never appear), the tilings are shown in the second picture of Figure 18. Depending on the space between two flips, there are $\lfloor \frac {k+3}{2} \rfloor $ or $\lfloor \frac {f+16}{12} \rfloor $ different tilings with the same set of vertices.

If $\beta \gamma ^3$ appears ( $\beta ^{k+1}\gamma ^2,\beta ^{2k+1}\gamma ,\beta ^{\frac {f}{2}}$ never appear), the tiling is shown in Figure 19. We obtain a unique tiling $T((6k-4)\alpha \gamma \delta ,2\beta \gamma ^3,6\alpha \beta ^{k}\delta )$ which can be obtained by applying the first flip modification three times.

Figure 19 $T((6k-4)\alpha \gamma \delta ,2\beta \gamma ^3,6\alpha \beta ^{k}\delta )$ obtained by flipping three times.

All of the above tilings belong to the third infinite sequence in Table 2 after interchanging $\alpha \leftrightarrow \delta $ and $\beta \leftrightarrow \gamma $ to keep consistent the AVC for two-layer earth map tilings.

If the ${\textit {AVC}}\subset \{\alpha \gamma \delta ,\alpha \beta ^{k}\delta \}$ , there is no solution satisfying Balance Lemma 2.6.

4.2 Case $2$ : $\{x_1, x_2\}=\{ x_3, x_4\}$

By Proposition 2.9, $\beta \neq \gamma $ . So the only possibility is that $x_1=x_3$ and $x_2=x_4$ in (4.1). After an easy check of the seven choices in (4.1), only the last one might hold: $2-\alpha -\frac \gamma 2=\frac \gamma 2$ and $\frac \gamma 2=1-\delta -\frac \beta 2$ . Then we get $\alpha +\beta +\gamma +\delta =3>\frac 83$ , a contradiction.

4.3 Case $3$ : $\{x_1, x_2\}=\{ \frac {1}{6},\theta \}$ and $\{x_3,x_4\}=\{\frac {\theta }{2},\frac {1}{2}-\frac {\theta }{2}\}$ , or $\{x_3,x_4\} = \{\frac {1}{6},\theta \}$ and $\{x_1,x_2\}=\{\frac {\theta }{2},\frac {1}{2}-\frac {\theta }{2}\}$ , for some $0<\theta \le \frac {1}{2}$

In the seven choices of (4.1), if $\frac {\gamma }{2}=\frac 16$ , then $\gamma =\frac 13$ , contradicting Lemma 4.1; if $\frac \gamma 2=\frac \theta 2$ and $\frac {\beta }{2}=\theta $ , then $\gamma <\beta $ , contradicting Lemma 4.1. Therefore, we only have $5\times 7=35$ options to consider. It turns out $27$ of these options are dismissed by Lemmas 2.1 and 4.1. We list the corresponding details in the right-hand column of Table 6. The remaining eight options are summarized as the following six subcases:

1. 1. $\alpha =1+\frac {\gamma }{2},\,\,\quad \beta =\frac {1}{3},\quad \quad \,\,\quad \delta =\frac {1}{3}-\frac {\gamma }{2},\quad \,\,\frac 13<\gamma <\frac 23$ ;

2. 2. $\alpha =2-\frac {3\gamma }{2}, \quad \beta =\frac {1}{3},\quad \quad \quad \,\, \delta =\frac {1}{3}-\frac {\gamma }{2},\quad \,\,\frac 13<\gamma <\frac 23$ ;

3. 3. $\alpha =\frac {3\gamma }{2}, \quad \quad \,\,\,\,\beta =\frac {1}{3},\quad \quad \quad \,\, \delta =\frac {2}{3}-\frac {\gamma }{2},\quad \,\,\frac 23<\gamma <1$ ;

4. 4. $\alpha =\frac 56+\frac {\gamma }{2},\quad \,\, \beta =2-2\gamma ,\quad \delta =\frac {3}{2}-\frac {3\gamma }{2},\quad \frac 56\le \gamma <1$ ;

5. 5. $\alpha =\frac 12+\frac {3\gamma }{4},\quad \beta =\frac {\gamma }{2},\quad \quad \quad \, \delta =\frac {1}{6}+\frac {\gamma }{4},\quad \,\,\frac 23<\gamma \le \frac 45$ ;

6. 6. $\alpha =\frac 32-\frac {\gamma }{4},\quad \,\, \beta =\frac {\gamma }{2},\quad \quad \quad \, \delta =\frac {1}{6}-\frac {\gamma }{4},\quad \,\,\frac 13<\gamma <\frac 23$ .

Table 6 Case $\{x_1, x_2\}=\{ \frac {1}{6},\theta \}$ and $\{x_3,x_4\}=\{\frac {\theta }{2},\frac {1}{2}-\frac {\theta }{2}\}$ or $\{x_3,x_4\}=\{\frac {1}{6},\theta \}$ and $\{x_1,x_2\}=\{\frac {\theta }{2},\frac {1}{2}-\frac {\theta }{2}\}$ , for some $0<\theta \le \frac {1}{2}$

For the first, second, and sixth subcases, we have $\beta ,\gamma <R(\alpha \delta \cdots )$ ; for the third, fourth, and fifth subcases, we have $\beta <R(\alpha \delta \cdots )<\gamma $ . So neither $\alpha \beta \delta $ nor $\alpha \gamma \delta $ is a vertex, contradicting Lemma 2.11.

4.4 Case $4$ : $\{ x_1,x_2,x_3,x_4\}$ are in Table 3

There are $8\times 7\times 15=840$ subcases to consider, but most are ruled out by violating $2>\alpha >1>\gamma >\beta >\delta >0$ , $\gamma>\frac 13$ , $\delta <\frac 12$ or f being even integer. Such computations can be carried out efficiently by any spreadsheet program. Only $29$ subcases are left in Table 7. But $26$ of them are ruled out by Lemma 2.11: there is neither $\alpha \beta \delta $ nor $\alpha \gamma \delta $ . There are only three subcases left: $(17,5,9,4)/15$ , $(41,10,16,3)/30$ , $(43,6,16,1)/30$ . They all imply $\alpha \cdots =\alpha \gamma \delta $ by the angle values and Parity Lemma. There is only one solution satisfying Balance Lemma 2.6: $\{f\alpha \gamma \delta ,2\beta ^{\frac {f}{2}}\}$ , and it gives three two-layer earth map tilings in Table 1 after interchanging $\alpha \leftrightarrow \delta $ and $\beta \leftrightarrow \gamma $ by Lemma 2.10.

Table 7 All $29$ solutions induced from Table 3

5 Degenerate case $\alpha =1$

If $\alpha =1$ , the quadrilateral degenerates to an isosceles triangle in Figure 20.

Figure 20 Degenerate case $\alpha =1$ and the subcase $\gamma +\delta =1$ .

Then $\beta =\delta $ , and Lemma 2.2 implies $\beta <\gamma $ . By Lemma 2.11, exactly one of $\alpha \beta \delta $ or $\alpha \gamma \delta $ must be a vertex in any spherical tiling by congruent such quadrilaterals.

5.1 Subcase $\alpha \beta \delta $ is a vertex

By Lemma 2.1, we get $\beta =\delta =\frac 12,\gamma =\frac {4}{f}$ . Then $\beta <\gamma $ implies $f=6$ and $\gamma =\frac 23$ . So the ${\textit {AVC}}=\{\alpha \beta \delta ,\gamma ^3\}$ , and it gives a two-layer earth map tiling by Lemma 2.10. This is Case $(6,3,4,3)/6$ in Table 1.

5.2 Subcase $\alpha \gamma \delta $ is a vertex

By Lemma 2.1, we get $\beta =\delta =\frac {4}{f},\gamma =1-\frac {4}{f}$ . Then $\beta <\gamma $ implies $f>8$ and $\gamma>\frac 12$ . By the angle values and Parity Lemma, we get the ${\textit {AVC}}\subset \{\alpha \gamma \delta ,\gamma ^3,\beta ^2\gamma ^2,\alpha \beta ^{\frac {f-4}{4}}\delta ,\beta ^{\frac {f+4}{4}}\gamma ,\beta ^{\frac {f}{2}}\}$ .

When $f=4k+2(k\ge 2)$ , we have the ${\textit {AVC}}\subset \{\alpha \gamma \delta ,\gamma ^3,\beta ^2\gamma ^2,\beta ^{\frac {f}{2}}\}$ , and the only solution satisfying Balance Lemma 2.6 is $\{ f\alpha \gamma \delta ,2\beta ^{\frac {f}{2}}\}$ which gives a two-layer earth map tiling by Lemma 2.10 ^′.

When $f=4k \ (k\ge 3)$ , we have $\gamma =(k-1)\beta $ , $\alpha +\delta =(k+1)\beta $ and the

$$\begin{align*}{\textit{AVC}}\subset\{\alpha\gamma\delta,\gamma^3,\beta^2\gamma^2,\alpha\beta^{k-1}\delta, \beta^{k+1}\gamma,\beta^{\frac{f}{2}}\}.\end{align*}$$

Trying out all possible $\beta $ -vertices as the previous section, there are always four tilings as shown in Figure 10 ^′, the second picture of Figure 21 (flip once), Figure 22 (flip twice with different spacing). Only when $f=12$ , we can apply the first flip modification in Figure 5 (after interchanging $\alpha \leftrightarrow \delta $ and $\beta \leftrightarrow \gamma $ ) three times, as shown in the first picture of Figure 21. This is because $3(k-1)>2k$ when $k\ge 4$ .

Figure 21 Two degenerate $a^3b$ -tilings.

Figure 22 Two tilings for $\{(4k-4)\alpha \gamma \delta ,2\beta ^2\gamma ^2,4\alpha \beta ^{k-1}\delta \}$ .

All above tilings belong to the first infinite sequence in Table 2.

6 Concave case $\beta>1$

The quadrilateral with $\beta>1$ is shown in Figure 23. We first prove some basic facts. Recall that Lemma 2.4 ^′ implies $\gamma +2\delta>1$ .

Figure 23 $a^3b$ -quadrilateral with $\beta>1,\alpha ,\gamma ,\delta <1$ .

Lemma 6.1. In an $a^3b$ -tiling with $\beta>1$ , we have $a<b$ , $\alpha <\gamma ,\delta $ and $\alpha <\frac 12$ .

Proof. In Figure 23, by $\beta>\delta $ , $\angle ABD=\beta -\psi>\delta -\psi =\angle ADB$ . This implies $a<b$ . Then $\angle CAD<\angle ACD$ , that is, $\alpha +\phi <\gamma +\phi $ . So $\alpha <\gamma $ . By Lemma 2.2 ^′, $\alpha <\delta $ . If $\alpha \ge \frac 12$ , then $\gamma ,\delta>\frac 12$ , and there is no $\beta \cdots $ vertex. So $\alpha <\frac 12$ .

Lemma 6.2. In an $a^3b$ -tiling with $\beta>1$ , $\beta \delta \cdots $ is a vertex and $\beta +\delta <2$ .

Proof. If $\beta \delta \cdots $ is not a vertex, by $\beta>1$ and Parity Lemma, we get $\beta \cdots =\alpha ^x\beta ,\alpha ^y\beta \gamma ^z,\beta \gamma ^w(x,y,w\ge 2,z\ge 1)$ . Then $\#\alpha +\#\gamma \ge 2\#\beta =2f$ , and there is only one solution satisfying Balance Lemma 2.6: $\{\frac f2\,\alpha ^2\beta ,\frac f2\, \beta \gamma ^2,\frac {f}{k}\,\delta ^k\}$ . But this implies $\alpha =\gamma $ , contradicting Lemma 2.3 ^′. Therefore, $\beta \delta \cdots $ is a vertex.

To find rational $a^3b$ -quadrilaterals by solving (2.5) or (2.6) via Proposition 2.14, we have to transform $\alpha -\frac {\gamma }{2},\frac \beta 2,\frac \gamma 2,\delta -\frac \beta 2,\alpha +\frac \gamma 2,-\delta -\frac \beta 2$ to the range $[0,\frac 12]$ . For (2.5), by Lemma 6.1, we have $-\frac 12<\alpha -\frac {\gamma }{2}<\frac 12,\frac 12<\frac {\beta }{2}<1,0<\frac {\gamma }{2}<\frac 12$ and $-1<\delta -\frac {\beta }{2}<\frac 12$ . For (2.6), by Lemma 6.1, we have $0<\alpha +\frac {\gamma }{2}<1,\frac 12<\frac \beta 2<1,0<\gamma <\frac 12$ , which implies $\sin (\delta +\frac \beta 2)<0$ . By $\frac 12<\delta +\frac {\beta }{2}<2$ , we get $1<\delta +\frac {\beta }{2}<2$ . If $\frac 32\le \delta +\frac {\beta }{2}<2$ , we get $\beta +\delta>2$ , contradicting Lemma 6.2. So for the equation (2.6), we have $0<\alpha +\frac {\gamma }{2}<1,\frac 12<\frac {\beta }{2}<1,0<\frac {\gamma }{2}<\frac 12$ and $1<\delta +\frac {\beta }{2}<\frac 32$ . Thus, we have to consider the following five choices:

(6.1) $$ \begin{align} \{ x_1, x_2, x_3, x_4\}=\begin{cases} \{\alpha-\frac{\gamma}{2},1-\frac{\beta}{2},\frac{\gamma}{2},\delta-\frac{\beta}{2}\}, \\ \{-\alpha+\frac{\gamma}{2},1-\frac{\beta}{2},\frac{\gamma}{2},1+\delta-\frac{\beta}{2}\}, \\ \{-\alpha+\frac{\gamma}{2},1-\frac{\beta}{2},\frac{\gamma}{2},-\delta+\frac{\beta}{2}\}, \\ \{\alpha+\frac{\gamma}{2},1-\frac{\beta}{2},\frac{\gamma}{2},-1+\delta+\frac{\beta}{2}\}, \\ \{1-\alpha-\frac{\gamma}{2},1-\frac{\beta}{2},\frac{\gamma}{2},-1+\delta+\frac{\beta}{2}\}. \\ \end{cases} \end{align} $$

We will match these choices with four cases of solutions in Proposition 2.14 as follows.

6.1 Case $1$ : $x_1 x_2=x_3 x_4=0$

By $-1<\delta -\frac {\beta }{2}<\frac 12$ , $-\frac 12<\alpha -\frac {\gamma }{2}<\frac 12$ and $1<\delta +\frac \beta 2<\frac 32$ , the only solution of $x_1 x_2=x_3 x_4=0$ for (6.1) comes from $\alpha =\frac {\gamma }{2},\delta =\frac {\beta }{2}$ . Then we get $3\alpha +\beta +\delta>2$ . By $R(\beta \delta \cdots )<3\alpha ,\beta ,\delta $ , Parity Lemma and Lemma 6.2, we deduce that $\alpha \beta \delta $ is a vertex. This implies $\alpha =\frac {2}{f},\beta =\frac 43-\frac {4}{3f},\gamma =\frac {4}{f},\delta =\frac 23-\frac {2}{3f}$ . By the angle values and Parity Lemma, we get the ${\textit {AVC}}\subset \{\alpha \beta \delta ,\alpha \delta ^3,\alpha ^x\beta \gamma ^{\frac {f-3x+2}{6}},\alpha ^y\gamma ^{\frac {f-3y+2}{6}}\delta ^2,\alpha ^z\gamma ^{\frac {2f-3z+1}{6}}\delta ,\alpha ^w\gamma ^{\frac {f-w}{2}}\}$ . Then we know there is no $\beta ^2\cdots $ vertex, which further implies that (by AAD) the

$$\begin{align*}{\textit{AVC}}\subset\{\alpha\beta\delta,\alpha\delta^3,\alpha^2\beta\gamma^{\frac{f-4}{6}},\alpha^2\gamma^{\frac{f-4}{6}}\delta^2,\beta\gamma^{\frac{f+2}{6}} ,\gamma^{\frac{f+2}{6}}\delta^2,\alpha\gamma^{\frac{f-1}{3}}\delta,\gamma^{\frac{f}{2}}\}.\end{align*}$$

When $f=6k$ or $6k+2 \ (k\ge 1)$ , we have the ${\textit {AVC}}\subset \{\alpha \beta \delta ,\alpha \delta ^3,\gamma ^{\frac {f}{2}}\}$ , and the only solution satisfying Balance Lemma 2.6 is $\{ f\alpha \beta \delta ,2\gamma ^{\frac {f}{2}}\}$ which gives a two-layer earth map tiling by Lemma 2.10.

When $f=6k+4 \ (k\ge 1)$ , we have $\beta =(2k+1)\gamma $ , $\alpha +\delta =(k+1)\gamma $ and the

$$\begin{align*}{\textit{AVC}}\subset\{\alpha\beta\delta,\alpha\delta^3,\alpha^2\beta\gamma^{k} ,\alpha^2\gamma^{k}\delta^2,\beta\gamma^{k+1},\gamma^{k+1}\delta^2, \alpha\gamma^{2k+1}\delta,\gamma^{\frac{f}{2}}\}.\end{align*}$$

We will discuss all possible $\gamma $ -vertices in any tiling as follows. Whenever $\gamma ^{\frac {f}{2}}$ is a vertex, the tiling must be a two-layer earth map tiling by Lemma 2.10. If $\gamma ^{\frac {f}{2}}$ never appears, we have the following subcases.

6.1.1 Subcase $\alpha ^2\beta \gamma ^{k}$ appears ( $\gamma ^{\frac {f}{2}}$ never appears)

By the AVC, $\beta ^2\cdots $ is never a vertex. Then $\alpha ^2\beta \gamma ^{k}$ has only two possible AAD. In Figure 24, $\alpha ^2\beta \gamma ^{k}=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma ^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha ^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\delta }\alpha ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ determines $T_1,T_2,T_3,T_4$ . Then $\beta _2\delta _1\cdots =\alpha _5\beta _2\delta _1$ determines $T_5$ . So $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _5\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots = \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _5\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\cdots $ , $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _5\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma ^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ or $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _5\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ . If $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _5\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots = \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _5\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\cdots $ or $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _5\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma ^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ , we get $\delta _2\delta _3\cdots = \beta \delta _2\delta _3\cdots $ , contradicting the AVC. So we have $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _5\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots = \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _5\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ which determines $T_6$ . Similarly, we can determine $T_7,T_8$ . Then we get $\delta _2\delta _3\delta _6\delta _7\cdots $ , contradicting the AVC. Therefore, $\alpha ^2\beta \gamma ^{k} = \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma ^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha ^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\delta }\alpha ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ .

Figure 24 One possible AAD of $\alpha ^2\beta \gamma ^{k}= \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma ^{\delta } \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha ^{\delta } \hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\delta }\alpha ^{\beta } \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma ^{\beta } \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ .

The AAD $\alpha ^2\beta \gamma ^{\frac {f-4}{6}}=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma _1^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha _2^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\delta }\alpha _3^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ determines $T_1,T_2,T_3$ in Figure 25. Then $R(\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots )=\gamma ^{k}$ and this $\gamma ^{k}$ determines k time zones ( $2k$ or $\frac {f-4}{3}$ tiles). We have $\beta _6\gamma _2\cdots =\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _6\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha ^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\cdots $ , $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _6\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma ^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ or $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _6\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ . If $\beta _6\gamma _2\cdots =\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _6\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha ^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\cdots $ or $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _6\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma ^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ , then we get $\beta \delta _2\delta _3\cdots $ , contradicting the AVC. Therefore, $\beta _6\gamma _2\cdots =\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _6\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ . This determines $T_7$ . Then $\delta _2\delta _3\delta _7\cdots =\alpha _8\delta _2\delta _3\delta _7$ determines $T_8$ . We have $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _6\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _7\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots =\alpha ^2\beta \gamma ^{k}$ or $\beta \gamma ^{k+1}$ . If $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _6\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _7\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots =\alpha ^2\beta \gamma ^{k}=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha \hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _6\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma _7^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ , this gives a vertex $\beta ^2\cdots $ , contradicting the AVC. Therefore, $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _6\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _7\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots =\beta \gamma ^{k+1}=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _6\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma _7^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ determines $T_9$ . Then $R(\beta _6\gamma _2\cdots )=\gamma ^{k}$ and this $\gamma ^{k}$ determines k time zones ( $2k$ or $\frac {f-4}{3}$ tiles). Similarly, we get $\beta _8\gamma _3\cdots =\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _8\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma _3^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma _{10}^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots =\beta \gamma ^{k+1}$ which determines $T_{10}$ . Then $R(\beta _8\gamma _3\gamma _{10}\cdots )=\gamma ^{k-1}$ and this $\gamma ^{k-1}$ determines $k-1$ time zones ( $2k-2$ or $\frac {f-10}{3}$ tiles). Then $\beta _3\delta _{10}\cdots =\alpha _{12}\beta _3\delta _{10}$ determines $T_{12}$ . So only two tiles are undetermined. By checking all possibilities, it turns out there are $3$ different ways to arrange these last two tiles, and Figure 25 shows one way with $\beta _{11}\gamma ^{\frac {f-4}{6}}\cdots =\beta \gamma ^{\frac {f+2}{6}}$ . Then $\alpha _9\delta \cdots =\alpha _9\beta _{14}\delta $ determines $T_{14}$ ; $\alpha _{14}\beta _{9}\gamma ^{\frac {f-4}{6}}\cdots =\alpha _{14}\alpha _{15}\beta _{9}\gamma ^{\frac {f-4}{6}},\alpha _{11}\delta _{14}\delta \cdots =\alpha _{11}\delta _{14}\delta _{15}\delta ,\beta _4\gamma ^{\frac {f-4}{6}}\cdots =\beta _4\gamma ^{\frac {f-4}{6}}\gamma _{15},\alpha _4\delta _{5}\cdots =\alpha _4\beta _{15}\delta _{5}$ determine $T_{15}$ . Centering $T_{14}, T_{15}$ in Figure 26, it becomes clear that they form a hexagon with three-fold symmetry, and the other two ways are obtained by rotating the b-edge $120^{\circ }$ and $240^{\circ }$ , respectively.

Figure 25 One special tiling for $\{(6k-2)\alpha \beta \delta ,2\alpha \delta ^3,2\alpha ^2\beta \gamma ^{k},4\beta \gamma ^{k+1}\}$ .

6.1.2 Subcase $\alpha \gamma ^{2k+1}\delta $ appears ( $\alpha ^2\beta \gamma ^k,\gamma ^{\frac {f}{2}}$ never appear)

If $\alpha ^2\beta \gamma ^k,\gamma ^{\frac {f}{2}}$ never appear, Balance Lemma 2.6 implies the

$$\begin{align*}{\textit{AVC}}\subset\{\alpha\beta\delta,\alpha^2\gamma^{k}\delta^2,\beta\gamma^{k+1},\alpha\gamma^{2k+1}\delta\}.\end{align*}$$

In Figure 27, we have the unique AAD $\alpha \gamma ^{2k+1}\delta =\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma _1^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha _2^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\alpha }\delta _3^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma _4^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ which determines $T_2,T_3$ . Then $R(\alpha _2\delta _3\cdots )=\gamma ^{2k+1}$ and this $\gamma ^{2k+1}$ determines $2k+1$ time zones ( $4k+2$ or $\frac {2f-2}{3}$ tiles). Then $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _4\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma _3^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots =\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _4\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma _3^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots =\beta \gamma ^{k+1}$ . Then $R(\beta _4\gamma _3\cdots )=\gamma ^{k}$ and this $\gamma ^{k}$ determines k time zones ( $2k$ or $\frac {f-4}{3}$ tiles). This tiling is exactly the second flip modification in Figure 5.

Figure 26 Three special tilings for $\{(6k-2)\alpha \beta \delta ,2\alpha \delta ^3,2\alpha ^2\beta \gamma ^{k},4\beta \gamma ^{k+1}\}$ .

Figure 27 $T((6k+2)\alpha \beta \delta ,2\beta \gamma ^{k+1},2\alpha \gamma ^{2k+1}\delta )$ .

6.1.3 Subcase $\alpha ^2\gamma ^{k}\delta ^2$ appears ( $\alpha ^2\beta \gamma ^k,\alpha \gamma ^{2k+1}\delta ,\gamma ^{\frac {f}{2}}$ never appear)

By the AVC, $\beta ^2\cdots $ is never a vertex. Then $\alpha ^2\gamma ^{k}\delta ^2$ has only two possible AAD. In Figure 28, $\alpha ^2\gamma ^{k}\delta ^2=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha _1^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\delta }\alpha _2^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma _3^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ determines $T_1,T_2,T_3$ . Then $\beta _2\delta _3\cdots =\alpha _4\beta _2\delta _3$ determines $T_4$ ; $\beta _4\gamma _2\cdots =\beta _4\gamma _2\gamma _5\cdots =\beta \gamma ^{k+1}$ . By $\gamma _5$ , we get $\beta \delta _1\delta _2\cdots $ or $\delta _1\delta _2\delta \cdots $ , contradicting the AVC. Therefore, $\alpha ^2\gamma ^{k}\delta ^2=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\delta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\delta \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ .

Figure 28 One possible AAD of $\alpha ^2\gamma ^{k}\delta ^2= \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\alpha \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ .

In Figure 29, $\alpha ^2\gamma ^{k}\delta ^2=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha _1^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\alpha }\delta _2^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma ^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha _3^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\alpha }\delta _4^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma ^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ determines $T_1,T_2,T_3,T_4$ . Then $R(\alpha ^2\delta ^2\cdots )=\gamma ^{k}$ determines k time zones ( $2k$ or $\frac {f-4}{3}$ tiles). Then $R(\beta \gamma _2\cdots )=R(\beta \gamma _4\cdots )=\gamma ^{k}$ and each of these two $\gamma ^{k}$ determines k time zones ( $2k$ or $\frac {f-4}{3}$ tiles). This tiling can also be obtained by applying the second flip modification in Figure 5 two times.

Figure 29 Many different tilings for $\{6k\alpha \beta \delta ,2\alpha ^2\gamma ^{k}\delta ^2,4\beta \gamma ^{k+1}\}$ .

If the ${\textit {AVC}}\subset \{\alpha \beta \delta ,\beta \gamma ^{k+1}\}$ , there is no solution satisfying Balance Lemma 2.6.

In fact, one special tiling in Figure 29, as shown in the first picture of Figure 30, is related to Figure 25 by a special flip modification along $L_3$ in Figure 30.

All of the above tilings belong to the second infinite sequence in Table 2.

6.2 Case $2$ : $\{x_1, x_2\}=\{ x_3, x_4\}$

We can fix $x_2=1- \frac \beta 2$ and $x_3=\frac \gamma 2$ in (6.1). Then either $x_1=x_3$ , $x_4=x_2$ as listed in the left of Table 8, or $x_1=x_4, x_2=x_3$ as listed in the right. All solutions are ruled out by the fact listed in the other column of Table 8 except one solution $-\alpha +\frac {\gamma }{2}=-\delta +\frac \beta 2$ , $1-\frac \beta 2=\frac \gamma 2$ . By $\beta +\gamma =2$ , we have $\beta \cdots =\alpha ^x\beta \delta ^y$ . By $\#\alpha +\#\delta \ge 2\#\beta =2f$ and $\alpha \neq \delta $ , there is only one solution satisfying Balance Lemma 2.6: $\{f\alpha \beta \delta ,2\gamma ^{\frac f2}\}$ . Then $\alpha =-\frac 12+\frac 4f,\beta =2-\frac 4f,\gamma =\frac 4f,\delta =\frac 12$ . By $\alpha>0$ , we get $f<8$ which forces $f=6$ . This solution admits only a two-layer earth map tiling $T(6\alpha \beta \delta ,2\gamma ^3)$ , and is Case $(1,8,4,3)/6$ in Table 1.

Table 8 All $10$ subcases of $\{x_1, x_2\}=\{ x_3, x_4\}$

6.3 Case $3$ : $\{x_1, x_2\}=\{ \frac {1}{6},\theta \}$ and $\{x_3,x_4\}=\{\frac {\theta }{2},\frac {1}{2}-\frac {\theta }{2}\}$ , or $\{x_3,x_4\} = \{\frac {1}{6},\theta \}$ and $\{x_1,x_2\}=\{\frac {\theta }{2},\frac {1}{2}-\frac {\theta }{2}\}$ , for some $0<\theta \le \frac {1}{2}$

In Table 9, we list each of these $5 \times 8=40$ options. It turns out $36$ of these options are dismissed by Lemma 2.1, Lemma 2.4 ^′, and Lemma 6.2. We list the corresponding details in the right-hand column. The remaining four options are summarized as follows:

1. 1. $\alpha =-\frac 16+\frac {\gamma }{2},\quad \beta =2\gamma ,\ \quad \quad \delta =-\frac 12+\frac {3\gamma }{2},\quad \frac {8}{15}<\gamma \le \frac 23$ ;

2. 2. $\beta =\frac 23+2\alpha ,\,\,\quad \gamma =\frac {1}{3},\hspace{4pt} \,\,\,\,\,\quad \quad \delta =3\alpha ,\quad \quad \quad \hspace{1pt}\,\,\,\,\,\,\frac 16<\alpha \le \frac {5}{18}$ ;

3. 3. $\alpha =\frac {3\gamma }{4},\,\,\quad \quad \quad \beta =1+\frac {\gamma }{2},\quad \delta =\frac {2}{3}+\frac {\gamma }{4},\quad \quad \,\frac {2}{15}<\gamma \le \frac 25$ ;

4. 4. $\alpha =\frac {\gamma }{4},\,\,\,\,\,\quad \quad \quad \beta =1+\frac {\gamma }{2},\quad \delta =\frac {1}{3}+\frac {\gamma }{4},\quad \quad \hspace{2pt}\,\,\,\,\frac {1}{3}<\gamma \le \frac 23$ .

Table 9 Case $\{x_1, x_2\}=\{ \frac {1}{6},\theta \}$ and $\{x_3,x_4\}=\{\frac {\theta }{2},\frac {1}{2}-\frac {\theta }{2}\}$ or $\{x_3,x_4\}=\{\frac {1}{6},\theta \}$ and $\{x_1,x_2\}=\{\frac {\theta }{2},\frac {1}{2}-\frac {\theta }{2}\}$ , for some $0<\theta \le \frac {1}{2}$

6.3.1 Subcase $\alpha =-\frac 16 + \frac {\gamma }{2},\beta =2\gamma ,\delta =-\frac 12+\frac {3\gamma }{2},\frac {8}{15}<\gamma \le \frac 23$

By the angle values and Parity Lemma, only $\alpha \beta \delta $ , $\beta \delta ^2$ and $\gamma ^3$ can be degree $3$ vertices. If $\beta \delta ^2$ is a vertex, we have $\alpha =\frac {2}{15}$ , $\beta =\frac 65$ , $\gamma =\frac 35$ , $\delta =\frac 25$ . Then $\beta \cdots =\beta \delta ^2$ , $\alpha ^3\beta \delta $ or $\alpha ^6\beta $ . So $\#\alpha +\#\delta>2\#\beta =2f$ , contradicting Balance Lemma 2.6. So $\alpha \beta \delta $ or $\gamma ^3$ is a vertex. Both cases imply $\alpha =\frac 16$ , $\beta =\frac 43$ , $\gamma =\frac 23$ , $\delta =\frac 12$ , and $f=6$ . This implies all vertices have degree $3$ . There is only one solution satisfying Balance Lemma 2.6: $\{6\alpha \beta \delta ,2\gamma ^3\}$ , and it gives a two-layer earth map tiling by Lemma 2.10. This also gives Case $(1,8,4,3)/6$ in Table 1 (see Remark 2.16).

6.3.2 Subcase $\beta =\frac 23+2\alpha ,\gamma =\frac {1}{3},\delta =3\alpha ,\frac 16<\alpha \le \frac {5}{18}$

By $R(\beta \delta \cdots )<3\alpha ,\beta ,\delta $ , Parity Lemma and Lemma 6.2, we get $\alpha \beta \delta $ is a vertex. This implies $\alpha =\frac 29,\beta =\frac {10}{9},\gamma =\frac 13,\delta =\frac 23$ . Then $\beta \cdots =\alpha \beta \delta ,\alpha ^4\beta $ . By $\#\beta =\#\alpha $ , we have $\beta \cdots =\alpha \beta \delta $ . There is only one solution satisfying Balance Lemma 2.6: $\{12\alpha \beta \delta ,2\gamma ^6\}$ , and it gives a two-layer earth map tiling by Lemma 2.10. This is Case $(2,10,3,6)/9$ in Table 1.

6.3.3 Subcase $\alpha =\frac {3\gamma }{4},\beta =1+\frac {\gamma }{2},\delta =\frac {2}{3}+\frac {\gamma }{4},\frac {2}{15}<\gamma \le \frac 25$

By $R(\beta \delta \cdots )<3\alpha ,\beta ,\delta $ , Parity Lemma and Lemma 6.2, we get $\alpha \beta \delta $ is a vertex. This implies $\alpha =\frac 16,\beta =\frac {10}{9},\gamma =\frac 29,\delta =\frac {13}{18}$ . Then $\alpha +\delta =4\gamma $ and $\beta =5\gamma $ . Then we get $f=18$ . By the angle values and Parity Lemma, we get the

$$\begin{align*}{\textit{AVC}}\subset\{\alpha\beta\delta,\alpha^2\gamma\delta^2,\beta\gamma^4,\alpha^4\beta\gamma,\alpha\gamma^5\delta,\alpha^5\gamma^2\delta,\gamma^9,\alpha^4\gamma^6,\alpha^8\gamma^3,\alpha^{12}\}.\end{align*}$$

By $\#\delta =\#\alpha $ , we have $\alpha \cdots =\delta \cdots =\alpha \beta \delta ,\alpha ^2\gamma \delta ^2$ or $\alpha \gamma ^5\delta $ . Therefore, the

$$\begin{align*}{\textit{AVC}}\subset\{\alpha\beta\delta,\alpha^2\gamma\delta^2,\beta\gamma^4,\alpha\gamma^5\delta,\gamma^9\}.\end{align*}$$

We will discuss all possible vertices containing $\gamma $ in any tiling as follows.

If $\gamma ^9$ appears, the tiling is a two-layer earth map tiling by Lemma 2.10. This is Case $(3,20,4,13)/18$ in Table 1.

If $\alpha \gamma ^5\delta $ appears ( $\gamma ^9$ never appears), then $\alpha \gamma ^5\delta =\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha _1^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\alpha }\delta _2^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma _3^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ determines $T_1,T_2,\dots ,T_7$ in Figure 31. Then $\beta _4\delta _3\cdots =\alpha _{8}\beta _4\delta _3$ determines $T_{8}$ . Similarly, we can determine $T_{9},T_{10},T_{11},T_{12}$ . Then $\beta _3\gamma _2\cdots =\beta _3\gamma _2\gamma _{13}\gamma _{14}\gamma _{15}$ . By $\gamma _{13}$ , we get $\beta _2\cdots =\beta _2\delta _{13}\cdots $ which determines $T_{13}$ . Similarly, we can determine $T_{14},T_{15}$ . Then $\beta _2\delta _{13}\cdots =\alpha _{16}\beta _2\delta _{13}$ and $\alpha _2\delta _1\cdots =\alpha _2\beta _{16}\delta _1$ determine $T_{16}$ . Similarly, we can determine $T_{17},T_{18}$ . This tiling is exactly the second flip modification in Figure 5.

Figure 30 A special flip modification ( $\frac {f+2}{3}$ tiles flipped).

Figure 31 $T(16\alpha \beta \delta ,2\beta \gamma ^4,2\alpha \gamma ^5\delta )$ .

If $\alpha ^2\gamma \delta ^2$ appears ( $\alpha \gamma ^5\delta $ , $\gamma ^9$ never appear), it has only two possible AAD since there is no vertex $\beta ^2\cdots $ by $\beta>1$ . In the first picture of Figure 32, $\alpha ^2\gamma \delta ^2=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha _1^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\delta }\alpha _2^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\delta _3^{\alpha }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\alpha }\delta _4^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma _5^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ determines $T_1,T_2,T_3,T_4,T_5$ . Then $\beta _1\delta _5\cdots =\alpha _6\beta _1\delta _5$ determines $T_6$ . We have $\beta _6\gamma _1\cdots =\beta _6\gamma _1\gamma _7\gamma ^2$ . By $\gamma _7$ , we have $\beta _7\delta _1\delta _2\cdots $ or $\delta _1\delta _2\delta _7\cdots $ , contradicting the AVC. In the second picture of Figure 32, $\alpha ^2\gamma \delta ^2=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha _1^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\alpha }\delta _2^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha _3^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\alpha }\delta _4^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma _5^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ determines $T_1,T_2,T_3,T_4,T_5$ . Then $\beta _1\delta _5\cdots =\alpha _6\beta _1\delta _5$ determines $T_6$ . Then $\beta _5\gamma _4\cdots =\beta _5\gamma _4\gamma _7\gamma _8\gamma _9$ . By $\gamma _7$ , we get $\beta _4\cdots =\beta _4\delta _7\cdots $ which determines $T_7$ . Similarly, we can determine $T_{8},T_{9}$ . Then $\beta _4\delta _{7}\cdots =\alpha _{10}\beta _4\delta _{7},\alpha _4\delta _3\cdots =\alpha _4\beta _{10}\delta _3$ determine $T_{10}$ . Similarly, we can determine $T_{11}$ , $T_{12}$ . After repeating the process one more time, we can determine $T_{13}$ , $T_{14}$ , $\dots $ , $T_{18}$ . This tiling can also be obtained by applying the second flip modification in Figure 5 two times.

Figure 32 $T(14\alpha \beta \delta ,2\alpha ^2\gamma \delta ^2,4\beta \gamma ^4)$ .

If the ${\textit {AVC}}\subset \{\alpha \beta \delta ,\beta \gamma ^4\}$ , there is no solution satisfying Balance Lemma 2.6.

6.3.4 Subcase $\alpha =\frac {\gamma }{4},\beta =1+\frac {\gamma }{2},\delta =\frac {1}{3}+\frac {\gamma }{4},\frac {1}{3}<\gamma \le \frac 23$

By $R(\beta \delta \cdots )<5\alpha ,\beta ,\delta $ , Parity Lemma and Lemma 6.2, we deduce that $\alpha \beta \delta $ or $\alpha ^3\beta \delta $ is a vertex. If $\alpha \beta \delta $ is a vertex, then $\alpha =\frac 16,\beta =\frac 43,\gamma =\frac 23,\delta =\frac 12$ . There is only one solution satisfying Balance Lemma 2.6: $\{6\alpha \beta \delta ,2\gamma ^3\}$ , and it gives a two-layer earth map tiling by Lemma 2.10. This also gives Case $(1,8,4,3)/6$ in Table 1. If $\alpha ^3\gamma \delta $ is a vertex, then $\alpha =\frac 19,\beta =\frac {11}{9},\gamma =\frac 49,\delta =\frac {4}{9}$ , which does not admit any any degree $3$ vertex, a contradiction.

6.4 Case $4$ : $\{ x_1,x_2,x_3,x_4\}$ are in Table 3

There are $8\times 5\times 15=600$ subcases to consider, but most are ruled out by violating $0<\alpha ,\gamma ,\delta <1,1<\beta <2$ , f being even integer or $\beta +\delta <2$ . Only 10 subcases are left in Table 10. But six of them are ruled out by not admitting any degree $3$ vertex. Four remaining subcases are boxed.

Table 10 All $10$ solutions induced from Table 3

6.4.1 Subcase $(5,32,6,23)/30$

By the angle values and Parity Lemma, we get $\beta \cdots =\alpha \beta \delta $ or $\alpha ^2\beta \gamma ^3$ . By $\#\beta =\#\alpha $ , we get $\beta \cdots =\alpha \beta \delta $ , which determines a two-layer earth map tiling $T(20\alpha \beta \delta ,2\gamma ^{10})$ in Table 1 by Lemma 2.10.

6.4.2 Subcase $(1,42,4,17)/30$

By the angle values and Parity Lemma, we get $\beta \cdots =\alpha \beta \delta $ , $\alpha ^2\beta \gamma ^4$ , $\alpha ^6\beta \gamma ^3$ , $\alpha ^{10}\beta \gamma ^2$ , $\alpha ^{14}\beta \gamma $ or $\alpha ^{18}\beta $ . By $\#\beta =\#\alpha $ , we get $\beta \cdots =\alpha \beta \delta $ , which determines a two-layer earth map tiling $T(30\alpha \beta \delta ,2\gamma ^{15})$ in Table 1 by Lemma 2.10.

6.4.3 Subcase $(1,21,5,8)/15$

By the angle values and Parity Lemma, we get $\beta \cdots =\alpha \beta \delta $ or $\alpha ^4\beta \gamma $ . By $\#\beta =\#\alpha $ , we get $\beta \cdots =\alpha \beta \delta $ , which determines a two-layer earth map tiling $T(12\alpha \beta \delta ,2\gamma ^{6})$ in Table 1 by Lemma 2.10.

6.4.4 Subcase $(5,32,14,13)/30$

By the angle values and Parity Lemma, we get $\beta \cdots =\beta \gamma ^2$ or $\alpha ^3\beta \delta $ . There is no solution satisfying Balance Lemma 2.6.

7 Degenerate case $\beta =1$

If $\beta =1$ , the quadrilateral degenerates to an isosceles triangle in Figure 33.

Figure 33 $\beta =1$ and the subcase $\alpha +\delta =1$ .

By $\beta =1$ , we have $\alpha +\gamma +\delta =(1+\frac {4}{f})$ . By Lemmas 2.2 ^′ and 2.4 ^′, we get $\delta>\alpha $ and $\gamma +2\delta>1$ . By $a+b>2a$ , we get $b>a$ . This implies $\gamma>\alpha $ . If $\alpha \ge \frac 12$ , then $R(\beta \cdots )=1\le 2\alpha <2\gamma ,2\delta $ . So $\beta \cdots =\alpha ^2\beta $ , contradicting Balance Lemma. We conclude that $\alpha <\frac 12$ and $\alpha ^2\beta $ is never a vertex.

If $\alpha \beta \delta $ is a vertex, we have $\alpha +\delta =1,\beta =1,\gamma =\frac 4f$ , as shown in the second picture of Figure 33. So $a=\frac 13$ , and we get $\alpha =\arctan ( 2\tan \frac {2\pi }{f} )$ by the cosine law. This is equivalent to $\cos (\frac {\pi }{2}-\alpha -\frac {2\pi }{f})-3\cos (\frac {\pi }{2}-\alpha +\frac {2\pi }{f})=0$ by the product to sum formula. Then Theorem $6$ of Conway–Jones [3] implies that $\alpha $ is irrational for any even integer $f\ge 6$ . Thus, this belongs to the irrational angle case in [11]. Such quadrilaterals always admit two-layer earth map tilings for any even integer $f\ge 6$ , together with their flip modifications when $f=4k$ as shown in Figure 34.

Figure 34 Two flips of $T(4k\alpha \beta \delta ,2\gamma ^{2k})$ if $\beta =1$ and $\alpha +\delta =1$ .

If $\alpha \beta \delta $ is not a vertex, then we will find all tilings by discussing all possible $\beta $ -vertices. If $\alpha ^x\beta (x\ge 4)$ is a vertex, then its unique AAD $\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\alpha ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha \hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\cdots $ at $\alpha ^x\beta (x\ge 4)$ gives a vertex $\beta ^2\cdots $ , contradicting $\beta =1$ . Similarly, $\alpha ^y\beta \delta (y\ge 5)$ , $\alpha ^w\beta \gamma (w\ge 4)$ , $\alpha ^p\gamma ^q(p\ge 2)$ and $\alpha ^z\delta ^2(z\ge 4)$ are not vertices.

7.0.1 Subcase $\gamma>\delta $

Then we have $\beta>\gamma >\delta >\alpha $ . By $\gamma +2\delta>1$ , we get $\gamma>\frac 13$ . By the angle values and Parity Lemma, we get $\beta \cdots =\beta \gamma ^2,\alpha ^2\beta \gamma ,\beta \delta ^x(x\ge 2)$ or $\alpha ^p\beta \delta ^q(p\ge 1,p+q\ge 4)$ .

If $\beta \gamma ^2$ is a vertex, then $\gamma =\frac 12,\alpha +\delta>\frac 12,\frac 14<\delta <\frac 12$ . So we have $\beta \cdots =\beta \gamma ^2$ , $\alpha ^2\beta \gamma $ or $\alpha ^3\beta \delta $ . They all satisfy $\#\alpha +\#\gamma \ge 2\#\beta $ . If $\alpha ^2\beta \gamma $ or $\alpha ^3\beta \delta $ is a vertex, then $\#\alpha +\#\gamma>2\#\beta $ , contradicting Balance Lemma 2.6. If $\beta \cdots =\beta \gamma ^2$ , then $\#\gamma>\#\beta $ , again a contradiction.

Therefore, we have $\beta \cdots =\alpha ^2\beta \gamma ,\beta \delta ^x$ or $\alpha ^p\beta \delta ^q$ . They all satisfy $\#\alpha +\#\delta \ge 2\#\beta =2f$ . There is only one solution satisfying Balance Lemma 2.6: $\{\frac {f}{2}\beta \delta ^2,\frac {f}{2}\alpha ^2\beta \gamma ,2\gamma ^{\frac f 4}\}$ . This implies $\alpha =\frac 12-\frac 4f$ , $\gamma =\frac 8f$ , $\delta =\frac 12$ . By $1>\gamma >\delta $ , we get $8<f<16$ , which do not satisfy (2.5) in Lemma 2.13. We conclude that there is no tiling in this case.

7.0.2 Subcase $\gamma <\delta $

Then we have $\beta>\delta >\gamma >\alpha $ . By $\gamma +2\delta>1$ , we get $\delta>\frac 13$ . By the angle values and Parity Lemma, we get $\beta \cdots =\beta \delta ^2,\alpha ^3\beta \delta ,\beta \gamma ^x(x\ge 2)$ or $\alpha ^p\beta \gamma ^q(p\ge 2,q\ge 1)$ .

If $\beta \delta ^2$ is a vertex, then $\gamma <\delta =\frac 12$ , $\alpha +\gamma>\frac 12$ . So $\beta \cdots =\beta \delta ^2,\alpha ^2\beta \gamma ,\alpha ^3\beta \delta $ or $\beta \gamma ^y(y\ge 3)$ . If $\alpha ^3\beta \delta $ is a vertex, then $\beta \cdots =\beta \delta ^2$ or $\alpha ^3\beta \delta $ . So $\#\alpha +\#\delta>2\#\beta $ , contradicting Balance Lemma 2.6. Similarly, $\beta \gamma ^y$ is not a vertex. So $\beta \cdots =\beta \delta ^2$ or $\alpha ^2\beta \gamma $ . There is only one solution satisfying Balance Lemma 2.6: $\{\frac {f}{2}\beta \delta ^2,\frac {f}{2}\alpha ^2\beta \gamma ,2\gamma ^{\frac f 4}\}$ . We get $\alpha =\frac 12-\frac {4}{f},\beta =1,\gamma =\frac {8}{f},\delta =\frac 12$ . By $\gamma <\delta $ , we get $f>16$ . By (2.5) in Lemma 2.13, we get $f=16$ , a contradiction.

If $\beta \delta ^2$ is not a vertex, we have $\beta \cdots =\alpha ^3\beta \delta ,\beta \gamma ^x$ or $\alpha ^p\beta \gamma ^q$ . They all satisfy $\#\alpha +\#\gamma \ge 2\#\beta $ . If $\alpha ^3\beta \delta $ or $\alpha ^p\beta \gamma ^q$ is a vertex, then $\#\alpha +\#\gamma>2\#\beta $ , contradicting Balance Lemma 2.6. If $\beta \cdots =\beta \gamma ^x$ , then $\#\gamma>\#\beta $ , again a contradiction.

7.0.3 Subcase $\gamma =\delta $

By $\gamma +2\delta>1$ , we get $\gamma =\delta>\frac 13$ . By the angle values and Parity Lemma, we get $\beta \cdots =\beta \gamma ^2,\beta \delta ^2,\alpha ^2\beta \gamma $ or $\alpha ^3\beta \delta $ . If $\beta \gamma ^2$ and $\beta \delta ^2$ are not vertices, we have $\beta \cdots =\alpha ^2\beta \gamma $ or $\alpha ^3\beta \delta $ , contradicting Balance Lemma 2.6. Therefore, $\beta \gamma ^2$ or $\beta \delta ^2$ is a vertex. So we get $\gamma =\delta =\frac 12$ . Then we get $\alpha =\frac {4}{f}$ . By $\gamma =\delta =\frac 12$ , we get $b=2a=\frac 12$ . By the sine law $ \frac {\sin \alpha }{\sin a}=\frac {\sin \gamma }{\sin 2a}$ , we have $\alpha =\frac 14$ . This implies $f=16$ . By the angle values and Parity Lemma, we get the

$$\begin{align*}{\textit{AVC}}\subset\{\beta\gamma^2,\beta\delta^2,\alpha^2\beta\gamma,\gamma^4,\gamma^2\delta^2,\delta^4,\alpha^2\gamma\delta^2\}.\end{align*}$$

If $\alpha ^2\gamma \delta ^2$ is a vertex, it has only two possible AAD. In the left of Figure 35, $\alpha ^2\gamma \delta ^2=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha _1^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\delta }\alpha _2^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\delta _3^{\alpha }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\alpha }\delta _4^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma _5^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ determines $T_1,T_2$ , $T_3,T_4,T_5$ . We have $\beta _2\gamma _3\cdots =\beta \gamma ^2$ or $\alpha ^2\beta \gamma $ . If $\beta _2\gamma _3\cdots =\alpha ^2\beta \gamma $ , we get the AAD $\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\alpha ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ at $\alpha ^2\beta \gamma $ . This gives a vertex $\beta ^2\cdots $ , contradicting the AVC. Therefore, $\beta _2\gamma _3\cdots =\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta _2^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma _3^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma _6^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ determines $T_6$ . Then $\beta _3\delta _6\cdots =\beta _3\delta _6\delta _7$ determines $T_7$ . Similarly, we can determine $T_8,T_9$ . Then we get $\alpha _3\alpha _4\gamma _7\gamma _8\cdots $ , contradicting the AVC.

Figure 35 Two possible $\alpha ^2\gamma \delta ^2$ and their AAD.

In the right of Figure 35, $\alpha ^2\gamma \delta ^2=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha _1^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\alpha }\delta _2^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha _3^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\cdots $ determines $T_1,T_2,T_3$ . We have $\beta _3\gamma _2\cdots =\beta \gamma ^2$ or $\alpha ^2\beta \gamma $ . If $\beta _3\gamma _2\cdots =\alpha ^2\beta \gamma $ , we get the AAD $\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\alpha ^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots $ at $\alpha ^2\beta \gamma $ . This gives a vertex $\beta ^2\cdots $ , contradicting the AVC. Therefore, $\beta _3\gamma _2\cdots =\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta _3^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma _2^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma _4^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ determines $T_4$ . Then $\beta _2\delta _4\cdots =\beta _2\delta _4\delta _5$ determines $T_5$ ; $\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _5\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha _2\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\delta _1\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots =\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\gamma _5\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha _2\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\delta _1\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\alpha _6\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\delta _7\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ determines $T_6,T_7$ . Similarly, we can determine $T_8$ . Then $\alpha _4\alpha _5\beta _8\cdots =\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha _4^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\delta }\alpha _5^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta _8^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma _9^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ determines $T_9$ . We get $\beta _4\gamma _3\delta _9\cdots $ , contradicting the AVC.

Therefore, $\alpha ^2\gamma \delta ^2$ is not a vertex. This implies $\alpha \cdots =\alpha ^2\beta \gamma $ .

If $\beta \gamma ^2$ is a vertex, it has only two possible AAD. In the first picture of Figure 36, $\beta \gamma ^2=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma _1^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma _2^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\alpha }\beta _3^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ determines $T_1,T_2,T_3$ . Then $\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\alpha _3\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots =\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\delta }\alpha _3^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta _2^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma _5^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha _4^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}$ determines $T_4,T_5$ ; $\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\alpha _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _5\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots =\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\delta }\alpha _2^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta _5^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma _6^{\delta } \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha _7^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}$ , $\beta _1\delta _2\delta _7\cdots =\beta _1\delta _2\delta _7$ determines $T_6,T_7$ ; $\beta _7\delta _6\cdots =\beta _7\delta _6\delta _8$ determines $T_8$ . We get $\alpha _1\gamma _7\gamma _8 \cdots $ , contradicting the AVC.

Figure 36 Two possible AAD for $\beta \gamma ^2$ .

In the second picture of Figure 36, $\beta \gamma ^2=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma _1^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\delta }\gamma _2^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\alpha }\beta _3^{\gamma }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ determines $T_1,T_2,T_3$ . Then $\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\alpha _3\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots =\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\delta }\alpha _3^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta _2^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma _5^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha _4^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}$ determines $T_4,T_5$ ; $\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}\alpha _2\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\beta _5\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}\cdots =\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\delta }\alpha _2^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta _5^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma _6^{\delta } \hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha _7^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}$ determines $T_6,T_7$ ; $\delta _1\delta _2\delta _7\cdots =\delta _1\delta _2\delta _7\delta _8$ determines $T_8$ ; $\beta _7\delta _6\cdots =\beta _7\delta _6\delta _9$ determines $T_9$ ; $\gamma _7\gamma _8\gamma _9\cdots =\gamma _7\gamma _8\gamma _9\gamma _{10}$ . We get $\beta _8\beta _{10}\cdots $ or $\beta _9\beta _{10}\cdots $ , contradicting the AVC.

Therefore, $\beta \gamma ^2$ is not a vertex.

This implies the ${\textit {AVC}}\subset \{\beta \delta ^2,\alpha ^2\beta \gamma ,\gamma ^4,\gamma ^2\delta ^2,\delta ^4\}$ . There is only one solution satisfying Balance Lemma 2.6: $\{8\beta \delta ^2,8\alpha ^2\beta \gamma ,2\gamma ^4\}$ . We have the AAD $\gamma ^4=\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma _1^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma _2^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma _3^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma _4^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ which determines $T_1,T_2,T_3$ , $T_4$ . Then $\beta _2\delta _1\cdots =\beta _2\delta _1\delta _5$ determines $T_5$ . Similarly, we can determine $T_6,T_7,T_8$ . Then $\alpha _2\alpha _6\gamma _5\cdots =\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\alpha _2^{\delta }\hspace {0.1em}\rule {1.5pt}{0.8em}\hspace {0.1em}^{\delta }\alpha _6^{\beta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\gamma }\beta _9^{\alpha }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}^{\beta }\gamma _5^{\delta }\hspace {0.1em}\rule {0.7pt}{0.8em}\hspace {0.1em}$ . So $\beta _5\cdots =\alpha _9\beta _5\cdots $ or $\beta _5\gamma _9\cdots $ , shown in two pictures of Figure 37, respectively.

Figure 37 Two tilings for $\{8\beta \delta ^2,8\alpha ^2\beta \gamma ,2\gamma ^4\}$ .

In the left of Figure 37, $\beta _5\cdots =\alpha _9\beta _5\cdots $ determines $T_9$ . Then $\alpha _3\alpha _7\gamma _6\cdots =\alpha _3\alpha _7\beta _{10}\gamma _6,\beta _6\gamma _9\cdots =\alpha _{10}\beta _6\gamma _9\cdots $ determine $T_{10}$ . Similarly, we can determine $T_{11},T_{12}$ . Then $ \alpha _9\beta _5\gamma _{12}\cdots =\alpha _9\alpha _{13}\beta _5\gamma _{12}$ determines $T_{13}$ . Similarly, we can determine $T_{14},T_{15},T_{16}$ .

In the right of Figure 37, $\beta _5\cdots =\beta _5\gamma _9\cdots $ determines $T_9$ . Then we get a different tiling by similar deductions. The $3$ D pictures for these two tilings are shown in Figure 3. Their authentic pictures of the stereo-graphic projection are shown in Figure 38. This is Case $(1,4,2,2)/4$ in Table 1.

Figure 38 Stereo-graphic projection for two tilings of $\{8\beta \delta ^2,8\alpha ^2\beta \gamma ,2\gamma ^4\}$ .