Article contents
TOPICS SURROUNDING THE COMBINATORIAL ANABELIAN GEOMETRY OF HYPERBOLIC CURVES IV: DISCRETENESS AND SECTIONS
Published online by Cambridge University Press: 18 January 2024
Abstract
Let 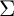 $\Sigma $ be a nonempty subset of the set of prime numbers which is either equal to the entire set of prime numbers or of cardinality one. In the present paper, we continue our study of the pro-
$\Sigma $ be a nonempty subset of the set of prime numbers which is either equal to the entire set of prime numbers or of cardinality one. In the present paper, we continue our study of the pro-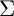 $\Sigma $ fundamental groups of hyperbolic curves and their associated configuration spaces over algebraically closed fields in which the primes of
$\Sigma $ fundamental groups of hyperbolic curves and their associated configuration spaces over algebraically closed fields in which the primes of 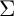 $\Sigma $ are invertible. The present paper focuses on the topic of comparison between the theory developed in earlier papers concerning pro-
$\Sigma $ are invertible. The present paper focuses on the topic of comparison between the theory developed in earlier papers concerning pro-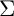 $\Sigma $ fundamental groups and various discrete versions of this theory. We begin by developing a theory concerning certain combinatorial analogues of the section conjecture and Grothendieck conjecture. This portion of the theory is purely combinatorial and essentially follows from a result concerning the existence of fixed points of actions of finite groups on finite graphs (satisfying certain conditions). We then examine various applications of this purely combinatorial theory to scheme theory. Next, we verify various results in the theory of discrete fundamental groups of hyperbolic topological surfaces to the effect that various properties of (discrete) subgroups of such groups hold if and only if analogous properties hold for the closures of these subgroups in the profinite completions of the discrete fundamental groups under consideration. These results make possible a fairly straightforward translation, into discrete versions, of pro-
$\Sigma $ fundamental groups and various discrete versions of this theory. We begin by developing a theory concerning certain combinatorial analogues of the section conjecture and Grothendieck conjecture. This portion of the theory is purely combinatorial and essentially follows from a result concerning the existence of fixed points of actions of finite groups on finite graphs (satisfying certain conditions). We then examine various applications of this purely combinatorial theory to scheme theory. Next, we verify various results in the theory of discrete fundamental groups of hyperbolic topological surfaces to the effect that various properties of (discrete) subgroups of such groups hold if and only if analogous properties hold for the closures of these subgroups in the profinite completions of the discrete fundamental groups under consideration. These results make possible a fairly straightforward translation, into discrete versions, of pro-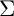 $\Sigma $ results obtained in previous papers by the authors. Finally, we discuss a construction that was considered previously by M. Boggi in the discrete case from the point of view of the present paper.
$\Sigma $ results obtained in previous papers by the authors. Finally, we discuss a construction that was considered previously by M. Boggi in the discrete case from the point of view of the present paper.
Keywords
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal
References
- 1
- Cited by


