No CrossRef data available.
Article contents
Über Einige Allgemeine Konvexitätssätze in der Theorie der Partiellen Differentialgleichungen
Published online by Cambridge University Press: 22 January 2016
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Es bezeichne Rn(n≥2) den durch den Alexandroff-Punkt kompaktifizierten n-dimensionalen euklidischen Raum, [xl,......,xn], ein Koordinatensystem von Rn, x = (x1,......,xn) einen (endlichen) Punkt von Rn und
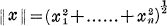
dessen Norm. Wir betrachten ein im Endlichen liegendes Gebiet G von Rn, definieren auf G einen linearen Operator
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1966
References
Literatur
BLASCHKE, W.: [1] Über eine Erweiterung des Satzes von Vitali über Folgen analytischer Funktionen. Leipz. Ber. 67, 1915, 194–200.Google Scholar
CARATHÉODORY, C: [1] Über die Winkelderivierten von beschränkten analytischen Funktionen. Sitzungsber. Preuss. Akad. d. Wissensch. Phys.-Math. Klasse, 1929, 34–54.Google Scholar
COURANT, R., HILBERT, D.: [1] Methods of Mathematical Physics, Vol. II, (Partial Differential Equations), Interscience Publishers, New-York-London, 1962.Google Scholar
DINGHAS, A.: [1] Über das Phargmén-Lindelöfsche Prinzip und den Julia-Carathéodoryschen Satz. Sitzungsber. d. PreuB. Akad. Wiss., Phys.-Math. Klasse, 1938, 32–48.Google Scholar
DINGHAS, A.: [2] Über positive harmonische Funktionen in einem Halbraum. Math. Zeitschr. 46, 1940, 559–570.Google Scholar
DINGHAS, A.: [3] Über das Anwachsen einiger Klassen von subharmonischen und verwandten Funktionen. Ann. Acad. Sci. Fenn. Ser. A I No. 336/1, 1963, 27 S.Google Scholar
DINGHAS, A.: [4] Über einige Konvexitätsfragen bei partiellen Differentialgleichungen vom Sturmschen Typus. Math. Ann. 155, 1964, S. 397–421.Google Scholar
DINGHAS, A.: [5] Über den EinfluB von Unendlichkeitsstellen auf das Wachstum subharmonischer Funktionen im En
. Monatsh. f. Math. 68, 1964, 289–306.Google Scholar
DINGHAS, A.: [6] Über einige Konvexitätssätze für die Mittelwerte von subharmonischen Funktionen. Journ. d. Math, pures et appl. (9), 44, 1965, S. 223–247.Google Scholar
PICARD, E.: [1] Leçons sur quelques types simples d’équations aux derivées partielles. Paris: Gauthier-Villars, 1927.Google Scholar
TSUJI, M.: [1] On a positiv harmonic function in a half plane. Jap. Journ. Math. 15, 1939, 277–285.Google Scholar
TSUJI, M.: [2] Potential Theory in Modern Functions Theory. Tokyo: Maruzen Co., Ltd. 1959.Google Scholar
VALLÉE POUSSIN, CH. de la: [1] Expression nouvelle d’une fonction harmonique positive dans une aire et nulle en tout autre point du bord sauf un. Annal. Soc. Bruxelles, A 53, 113–122.Google Scholar
WOLFF, J.: [1] Démonstration d’un théorème sur la conservation des angles dans la représentation conforme d’un domaine au voisinage du’n point frontière. Proc. Akad. Amsterdam
38, 1935, 46–50.Google Scholar
WOLFF, J.: [2] Sur la réprésentation conforme des bandes. Comp. Math. 1, 1935, 217—222.Google Scholar


