Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1975.
The Theory of Numbers.
Vol. 8,
Issue. ,
p.
519.
1989.
Topics in Field Theory.
Vol. 155,
Issue. ,
p.
477.

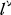 of a prime number
of a prime number 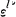 consisting of all
consisting of all