This is a continuation of [5]. In the present part, we study irregular even surfaces of general type with K < 4χ, where K and χ denote respectively a canonical divisor and the holomorphic Euler-Poincaré characteristic. As the first main theorem, we show the following:

In every network, many nodes with brains are connected by many links each other. Some nodes are, for example, computers, terminals, or routers. The both ends of a link can communicate directly each other. For example, local area network, in which every nodes are directly connected each other, looks like Figure 1, then every nodes can communicate directly to others.

Let (M, g) be a Kähler C-space. R and ∇ denote the curvature tensor and the Levi-Civita connection of (M, g), respectively.

In [6], Takagi have proved that there exists an integer n such that

We studied plane curves in Lie sphere geometry in [YY]. Especially we constructed Lie frames of curves in S2 and classified them by the Lie equivalence. In this paper we are concerned with surfaces in S3. We construct Lie frames and classify them. We moreover obtain the necessary and sufficient condition that two surfaces are Lie equivalent.

The Laplacians form a class of the most important differential operators in white noise analysis. The goal of this paper is to give their characterizations. Our main tools are the Fock expansions of operators in terms of integral kernel operators and rotation-invariance. In Section 1, the fundamental setting of white noise analysis is introduced briefly. In Section 2, integral kernel operators and the Fock expansions of operators are given. The characterization theorems for number operator, Gross-Laplacian and Euler operator are given in Sections 3, 4 and 5 respectively.

Let G be a connected linear algebraic group and X an algebraic variety, both defined over Q, the field of rational numbers. Suppose that G acts on X transitively and the action is defined over Q. Suppose that the set of rational points X(Q) is non-empty. Choosing x ∈ X(Q) allows us to identify G/Gx and X as varieties over Q, there Gx is the stabilizer of x.

Ce travail est consacré aux groupes d’automorphismes de certaines algebres quantiques de dimension 2 ou 3. Dans la théorie classique des algebres enveloppantes, si 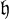désigne l’algèbre de Lie de Heisenberg de dimension 3, U(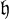) admet l’algèbre de Weyl A1 comme seul quotient primitif de dimension 2, avec les propriétés suivantes: d’ une part tout automorphisme de A1 se relève en un automor-phisme de U(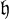), d’autre part U(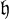) admet des automorphismes non modérés (cf. [A1], [Di1], [ML]). On retrouve la même situation pour les quotients primitifs minimaux de U(sl(2)) paramétrés par C (cf. [Di2], [Jo]). En outre, dans ce cas, on dispose des plongements de Conze de ces quotients dans A1 (cf. [Di2], [Co], [Ro]); bien que les groupes d’automorphismes soient comparables, la restriction correspondant à un tel plongement est seulement définie sur le sous-groupe des automorphismes triangulaires de A1 (cf. annexe).

Two very different definitions of a newform of half-integral weight are present and continued to be developed in the literature. The first definition originated with Serre and Stark for forms of weight 1/2 [5], and is analogous to the definition of newform for integral weight forms, which uses forms of lower level and shifts of such forms to characterize the notion of old-forms. The second definition originated with Kohnen for half-integral weight forms of squarefree level [1], who used forms of lower level and their image under the Um2 operator to define the notion of oldforms. The choice of the Um2 operator over the shift operator Bd seems a propitious one, since the U operator commutes with the action of the Shimura lift, while the shift operator B does not. More to the point, Kohnen was able to develop a newform theory on a distinguished subspace of the full space of cusp forms (now referred to as the Kohnen subspace), and obtained a multiplicity-one result (with respect to Hecke eigenvalues) for half-integral weight newforms in this subspace. Even nicer, the multiplicity-one result was established by showing that there is a one-to-one correspondence between newforms of level AN in the subspace and the newforms of integral weight of level N.

Let M be a compact non-singular real affine algebraic variety and let A, B be open disjoint semialgebraic subsets of M. Define (where —4 denotes the Zariski closure).

Let H, U be two real Hilbert spaces and let g be a proper lower semi-continuous convex function from L2 (0, T;H) into R+. For each t in [0, T], let φ(t,.) be a proper l.s.c. convex function from H into R with effective domain Dφ(t,.)) and let h be a l.s.c. convex function from a closed convex subset u of U into L2(0, T;H) with

for all u in U. The constants γ and C are positive.