Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dumas, François
and
Rigal, Laurent
2002.
PRIME SPECTRUM AND AUTOMORPHISMS FOR 2×2 JORDANIAN MATRICES.
Communications in Algebra,
Vol. 30,
Issue. 6,
p.
2805.
Richard, Lionel
2002.
SUR LES ENDOMORPHISMES DES TORES QUANTIQUES.
Communications in Algebra,
Vol. 30,
Issue. 11,
p.
5283.
Ben Yakoub, L.
El Kaoutit, L.
and
Malliavin, M. P.
2002.
SUR LES ALGÈBRES D'HEISENBERG QUANTIQUES.
Communications in Algebra,
Vol. 30,
Issue. 1,
p.
129.
RICHARD, LIONEL
and
SOLOTAR, ANDREA
2006.
ISOMORPHISMS BETWEEN QUANTUM GENERALIZED WEYL ALGEBRAS.
Journal of Algebra and Its Applications,
Vol. 05,
Issue. 03,
p.
271.
Lopes, Samuel A.
2006.
Primitive Ideals of.
Communications in Algebra,
Vol. 34,
Issue. 12,
p.
4523.
Launois, S.
and
Lenagan, T. H.
2007.
Primitive Ideals and Automorphisms of Quantum Matrices.
Algebras and Representation Theory,
Vol. 10,
Issue. 4,
p.
339.
Launois, Stéphane
and
Lopes, Samuel A.
2007.
Automorphisms and derivations of Uq(sl4+).
Journal of Pure and Applied Algebra,
Vol. 211,
Issue. 1,
p.
249.
LAUNOIS, STÉPHANE
2007.
PRIMITIVE IDEALS AND AUTOMORPHISM GROUP OF $U_{q}^{+}(B_{2})$.
Journal of Algebra and Its Applications,
Vol. 06,
Issue. 01,
p.
21.
Carvalho, Paula A. A. B.
and
Lopes, Samuel A.
2009.
Automorphisms of Generalized Down-Up Algebras.
Communications in Algebra,
Vol. 37,
Issue. 5,
p.
1622.
Launois, Stéphane
and
Lopes, Samuel A.
2013.
Classification of factorial generalized down–up algebras.
Journal of Algebra,
Vol. 396,
Issue. ,
p.
184.
Yakimov, Milen
2014.
Rigidity of quantum tori and the Andruskiewitsch–Dumas conjecture.
Selecta Mathematica,
Vol. 20,
Issue. 2,
p.
421.
Ceken, S.
Palmieri, J.H.
Wang, Y.-H.
and
Zhang, J.J.
2015.
The discriminant controls automorphism groups of noncommutative algebras.
Advances in Mathematics,
Vol. 269,
Issue. ,
p.
551.
Sinel'shchikov, S.D.
2015.
On symmetries of a quantum plane and its Laurent extension.
Reports of the National Academy of Sciences of Ukraine,
p.
22.
Gaddis, Jason
2015.
Two-Generated Algebras and Standard-Form Congruence.
Communications in Algebra,
Vol. 43,
Issue. 4,
p.
1668.
Keilberg, Marc
2015.
Automorphisms of the Doubles of Purely Non-Abelian Finite Groups.
Algebras and Representation Theory,
Vol. 18,
Issue. 5,
p.
1267.
Suárez-Alvarez, Mariano
and
Vivas, Quimey
2015.
Automorphisms and isomorphisms of quantum generalized Weyl algebras.
Journal of Algebra,
Vol. 424,
Issue. ,
p.
540.
Ceken, S.
Palmieri, J.H.
Wang, Y.-H.
and
Zhang, J.J.
2016.
The discriminant criterion and automorphism groups of quantized algebras.
Advances in Mathematics,
Vol. 286,
Issue. ,
p.
754.
Gaddis, Jason
2016.
Two-Parameter Analogs of the Heisenberg Enveloping Algebra.
Communications in Algebra,
Vol. 44,
Issue. 11,
p.
4637.
Li, Min
and
Wang, Xiu Ling
2017.
Derivations and automorphisms of the positive part of the two-parameter quantum group U r,s (B 3).
Acta Mathematica Sinica, English Series,
Vol. 33,
Issue. 2,
p.
235.
Gaddis, Jason
and
Price, Kenneth L.
2017.
Some algebras similar to the 2×2 Jordanian matrix algebra.
Communications in Algebra,
Vol. 45,
Issue. 5,
p.
2091.
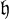 désigne l’algèbre de Lie de Heisenberg de dimension 3, U(
désigne l’algèbre de Lie de Heisenberg de dimension 3, U(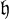 ) admet l’algèbre de Weyl A1 comme seul quotient primitif de dimension 2, avec les propriétés suivantes: d’ une part tout automorphisme de A1 se relève en un automor-phisme de U(
) admet l’algèbre de Weyl A1 comme seul quotient primitif de dimension 2, avec les propriétés suivantes: d’ une part tout automorphisme de A1 se relève en un automor-phisme de U(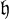 ), d’autre part U(
), d’autre part U(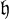 ) admet des automorphismes non modérés (cf. [A1], [Di1], [ML]). On retrouve la même situation pour les quotients primitifs minimaux de U(sl(2)) paramétrés par C (cf. [Di2], [Jo]). En outre, dans ce cas, on dispose des plongements de Conze de ces quotients dans A1 (cf. [Di2], [Co], [Ro]); bien que les groupes d’automorphismes soient comparables, la restriction correspondant à un tel plongement est seulement définie sur le sous-groupe des automorphismes triangulaires de A1 (cf. annexe).
) admet des automorphismes non modérés (cf. [A1], [Di1], [ML]). On retrouve la même situation pour les quotients primitifs minimaux de U(sl(2)) paramétrés par C (cf. [Di2], [Jo]). En outre, dans ce cas, on dispose des plongements de Conze de ces quotients dans A1 (cf. [Di2], [Co], [Ro]); bien que les groupes d’automorphismes soient comparables, la restriction correspondant à un tel plongement est seulement définie sur le sous-groupe des automorphismes triangulaires de A1 (cf. annexe).