Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T09:44:12.875Z Has data issue: false hasContentIssue false
  • English
  • Français

On an optimal control problem for a parabolic inclusion

Published online by Cambridge University Press:  22 January 2016

Bui an Ton
Bui an Ton*
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, V6T 1Z2, Canada, e-mail: bui@math.ubc.ca
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let H, U be two real Hilbert spaces and let g be a proper lower semi-continuous convex function from L2 (0, T;H) into R+. For each t in [0, T], let φ(t,.) be a proper l.s.c. convex function from H into R with effective domain Dφ(t,.)) and let h be a l.s.c. convex function from a closed convex subset u of U into L2(0, T;H) with

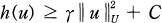
for all u in U. The constants γ and C are positive.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 143 , September 1996 , pp. 195 - 217
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1996

References

[ 1 ] Attouch, H. and Damlamian, A., Problemes d’evolution dans les Huberts et applications, J. Math. Pure Appl., 54 (1975), 53–74.Google Scholar
[ 2 ] Aubin, J. P., Mathematical methods of game and economic theory, Studies in Math. and its appl., 7 (1982), North Holland.Google Scholar
[ 3 ] Aubin, J. P. and Cellina, A., Differential inclusions, Springer-Verlag, Berlin-New York (1984).CrossRefGoogle Scholar
[ 4 ] Barbu, V. and Tiba, D., Optimal control of abstract variational inequalities, Amouroux et El Jai Eds. Pergamon Press, Oxford (1989).Google Scholar
[ 5 ] Barbu, V. and Neittaanmaki, P. and Niemisto, A., Approximating optimal control problems governed by variational inequalities, Numerical Func. Anal, and Optimization, 15 (5-6) (1994), 489–502.Google Scholar
[ 6 ] Brezis, H., Operateurs maximaux monotones et semigroupes de contractions dans les espaces de Hilbert, Math. Studies, 5 (1975), North Holland.Google Scholar
[ 7 ] Lions, J. L. and Magenes, E., Problemes aux limites non homogenes, Dunod-Gauthier-Villard, Pris (1968).Google Scholar
[ 8 ] Lukaszewicz, G. and Ton, Bui An, On some differential inclusions and their applications, J. Math. Sci. Univ. of Tokyo, 1, No 2 (1994), 369–391.Google Scholar
[ 9 ] Makhmudov, E. N. and Pshenichnyi, B. N., The optimal principle for discrete and differential inclusions of parabolic type with distributed parameters and duality, Izv. Akad. Nauk, 57 (1993) = Russian Acad. Sci. Izv. Math., 42 (1994), 299–319.Google Scholar
[10] Watanabe, J., On certain nonlinear evolution equations, J. Math. Soc. Japan, 25 (1973), 446–463.Google Scholar
[11] Yamada, Y., On evolution equations generated by subdifferential operators. J. Fac. Sci. Univ. of Tokyo, Sec IA. Math., 23 (1976), 491–515.Google Scholar
[12] Yamada, Y., Periodic solutions of certain nonlinear parabolic equations in domains with periodically moving boundaries, Nagoya Math. J., 70 (1978), 111 – 123.CrossRefGoogle Scholar