1. Introduction
Automatic language identification of text has been researched since the 1960s. It has been considered a subspecies of general text categorization and most of the methods used are similar to those used in categorizing text according to their topic. However, deep learning techniques have not proven to be as efficient in language identification as they have been in other categorization tasks (Medvedeva, Kroon, and Plank Reference Medvedeva, Kroon and Plank2017; Ali Reference Zampieri, Malmasi, Nakov, Ali, Shon, Glass, Scherrer, Samardži, Ljubešić, Tiedemann, van der Lee, Grondelaers, Oostdijk, van den Bosch, Kumar, Lahiri and Jain2018).
For the past 6 years, we have been developing a language identifying method, which we call HeLI, for the Finno-Ugric languages and the Internet project (Jauhiainen, Jauhiainen, and Lindén Reference Jauhiainen, Jauhiainen and Lindén2015a). The HeLI method is a supervised general-purpose language identification method relying on observations of word and character n-gram frequencies from a language labeled corpus. The method is similar to naive Bayes (NB) when using only relative frequencies of words as probabilities. Unlike NB, it uses a back-off scheme to approximate the probabilities of individual words if the words themselves are not found in the language models (LMs). As LMs, we use word unigrams and character level n-grams. The optimal combination of the LMs used with the back-off scheme depends on the situation and is determined empirically using a development set. The latest evolution of the HeLI method, HeLI 2.0, is described in this article.
One of the remaining difficult cases in language identification is the identification of language varieties or dialects. The task of language identification is less difficult if the set of possible languages does not include very similar languages. If we try to discriminate between very close languages or dialects, the task becomes increasingly more difficult (Tiedemann and Ljubešić Reference Tiedemann and Ljubešić2012). The first ones to experiment with language identification for close languages were Sibun and Reynar (Reference Sibun and Reynar1996) who had Croatian, Serbian, and Slovak as part of their language repertoire. The differences between definitions of dialects and languages are not usually clearly defined, at least not in terms which would be able to help us automatically decide whether we are dealing with languages or dialects. Furthermore, the methods used for dialect identification are most of the time exactly the same as for general language identification. During the last 5 years, the state-of-the-art language identification methods have been put to the test in a series of shared tasks as part of VarDial workshops (Zampieri et al. Reference Tan, Zampieri, Ljubešic and Tiedemann2014; Zampieri et al. Reference Zampieri, Tan, Ljubešić, Tiedemann and Nakov2015; Malmasi et al. Reference Malmasi, Zampieri, Ljubešić, Nakov, Ali and Tiedemann2016; Zampieri et al. Reference Malmasi and Zampieri2017; Zampieri et al. Reference Jauhiainen, Lui, Zampieri, Baldwin and Lindén2018). We have used the HeLI method and its variations in the shared tasks of the four latest VarDial workshops (Jauhiainen, Jauhiainen, and Lindén Reference Jauhiainen, Jauhiainen and Lindén2015b; Jauhiainen, Lindén, and Jauhiainen Reference Jauhiainen, Lindén and Jauhiainen2016; Reference Jauhiainen, Lindén and Jauhiainen2017a; Jauhiainen, Jauhiainen, and Lindén Reference Jauhiainen, Jauhiainen and Lindén2018a; Reference Jauhiainen, Jauhiainen and Lindén2018b; Reference Jauhiainen, Jauhiainen and Lindén2018c). The HeLI method has proven to be robust and it competes well with other state-of-the-art language identification methods.
Another remaining difficult case in language identification is the situation when the training data are not in the same domain as the data to be identified. Being out-of-domain can mean several things. For example, the training data can be from a different genre, different time period, and/or produced by different writers than the data to be identified. The identification accuracies are considerably lower on out-of-domain data (Li, Baldwin, and Cohn Reference Li, Baldwin and Cohn2018) depending on the degree of out-of-domainness. The extreme example of in-domainness is when the training data and test data are from different parts of the same text, as it has been in several language identification experiments in the past (Vatanen, Väyrynen, and Virpioja Reference Vatanen, Väyrynen and Virpioja2010; Brown Reference Brown2012; Brown Reference Brown2013; Brown Reference Brown2014). Classifiers can be more or less sensitive to the domain differences between the training and the testing data depending on the machine learning methods used (Blodgett, Wei, and O’Connor Reference Blodgett, Wei and O’Connor2017). One way to diminish the effects of the phenomena is to create domain-general LMs using adversarial supervision which reduces the amount of domain-specific information in the LMs (Li et al. Reference Li, Baldwin and Cohn2018). We suggest that another way to do this is to use active LM adaptation.
In LM adaptation, we use the unlabeled mystery text itself to enhance the LMs used by a language identifier. The LM adaptation scheme introduced in this article is not an off-line adaptation technique used to adapt an existing identifier to a particular domain; it is a general on-line adaptation technique that is used each time the language of a new text is to be identified. The language identification method used in combination with the LM adaptation approach presented in this article must be able to produce a confidence score of how well the identification has performed. As the LMs are updated regularly while the identification is ongoing, the approach also benefits from the language identification method being non-discriminative. If the method is non-discriminative, all the training materials do not have to be reprocessed when adding new information into the LMs. To the best of our knowledge, LM adaptation has not been used in language identification of digital text before the first versions of the method presented in this article were used in the shared tasks of the 2018 VarDial workshop (Jauhiainen et al. Reference Jauhiainen, Jauhiainen and Lindén2018a; Reference Jauhiainen, Jauhiainen and Lindén2018b; Reference Jauhiainen, Jauhiainen and Lindén2018c). Concurrently with our current work, Ionescu and Butnaru (Reference Jauhiainen, Jauhiainen and Lindén2018) presented an adaptive version of the Kernel Ridge Classifier which they evaluated on the Arabic Dialect Identification (ADI) dataset from the 2017 VarDial workshop (Zampieri et al. Reference Malmasi and Zampieri2017).
In this article, we first review the previous work relating to German dialect identification, Indo-Aryan language identification, and LM adaptation (Section 2). We then present the methods used in the article: the HeLI 2.0 method for language identification, three confidence estimation methods, and the algorithm for LM adaptation (Section 3). In Section 4, we introduce the datasets used for evaluating the methods, and in Section 5, we evaluate the methods and present the results of the experiments.
2. Related work
The first automatic language identifier for digital text was described by Mustonen (Reference Mustonen1965). Since this first article, hundreds of conference and journal articles describing language identification experiments and methods have been published. For a recent survey on language identification and the methods used in the literature, see Jauhiainen et al. (2018d). The HeLI method was first published in 2010 as part of a master’s thesis (Jauhiainen Reference Jauhiainen2010) and has since been used, outside the VarDial workshops, for language set identification (Jauhiainen, Lindén, and Jauhiainen 2015c) as well as general language identification with a large number of languages (Jauhiainen, Lindén, and Jauhiainen Reference Jauhiainen, Lindén and Jauhiainen2017b). One of the main strengths of the HeLI method is that it uses the word-level models and is still able to graciously deal with any possible out of vocabulary words that it encounters.
2.1 German dialect identification
German dialect identification has earlier been considered by Scherrer and Rambow (Reference Scherrer and Rambow2010), who used a lexicon of dialectal words. Hollenstein and Aepli (Reference Hollenstein and Aepli2015) experimented with a perplexitybased language identifier using character trigrams. They reached an average F-score of 0.66 on sentence level distinguishing between 5 German dialects.
The results of the first shared task on German dialect identification (GDI) are described by Zampieri et al. (Reference Malmasi and Zampieri2017). Ten teams submitted results on the task utilizing a variety of machine learning methods used for language identification. The team MAZA (Malmasi and Zampieri Reference Malmasi and Zampieri2017) experimented with different types of support vector machine (SVM) ensembles: plurality voting, mean probability, and meta-classifier. The meta-classifier ensemble using the Random Forest algorithm for classification obtained the best results. The team CECL (Bestgen Reference Bestgen2017) used SVMs as well, and their best results were obtained using an additional procedure to equalize the number of sentences assigned to each category. Team CLUZH experimented with NB, conditional random fields (CRF), as well as a majority voting ensemble consisting of NB, CRF, and SVM (Clematide and Makarov Reference Clematide and Makarov2017). Their best results were reached using CRF. Team qcri_mit used an ensemble of two SVMs and a stochastic gradient classifier (SGD). Team unibuckernel experimented with different kernels using kernel ridge regression (KRR) and kernel discriminant analysis (KDA) (Ionescu and Butnaru Reference Ionescu and Butnaru2017). They obtained their best results using KRR based on the sum of three kernels. Team tubasfs (Çöltekin and Rama Reference Çöltekin and Rama2017) used SVMs with features weighted using sublinear TF-IDF (product of term frequency and inverse document frequency) scaling. Team ahaqst used cross entropy (CE) with character and word n-grams (Hanani, Qaroush, and Taylor Reference Hanani, Qaroush and Taylor2017). Team Citius_Ixa_Imaxin used perplexity with different features (Gamallo, Pichel, and Alegria Reference Gamallo, Pichel and Alegria2017). Team XAC_Bayesline used NB (Barbaresi Reference Barbaresi2017) and team deepCybErNet Long Short-Term Memory (LSTM) neural networks. We report the F1-scores obtained by the teams in Table 8 together with the results presented in this article.
The second shared task on German dialect identification was organized as part of the 2018 VarDial workshop (Zampieri et al. Reference Jauhiainen, Lui, Zampieri, Baldwin and Lindén2018). We participated in the shared task with an earlier version of the method described in this article and our submission using the LM adaptation scheme reached a clear first place (Jauhiainen et al. Reference Jauhiainen, Jauhiainen and Lindén2018a). Seven other teams submitted results on the shared task. Teams Twist Bytes (Benites et al. Reference Benites, Grubenmann, von Däniken, von Grünigen, Deriu and Cieliebak2018), Tübingen-Oslo (Çöltekin, Rama, and Blaschke Reference Çöltekin, Rama and Blaschke2018), and GDI_classification (Ciobanu, Malmasi, and Dinu Reference Ciobanu, Malmasi and Dinu2018a) used SVMs. The team safina used convolutional neural networks (CNN) with direct one-hot encoded vectors, with an embedding layer, as well as with a Gated Recurrent Unit (GRU) layer (Ali Reference Zampieri, Malmasi, Nakov, Ali, Shon, Glass, Scherrer, Samardži, Ljubešić, Tiedemann, van der Lee, Grondelaers, Oostdijk, van den Bosch, Kumar, Lahiri and Jain2018). The team LaMa used a voting ensemble of eight classifiers. The best results for the team XAC were achieved using NB, but they experimented with Ridge regression and SGD classifiers as well (Barbaresi Reference Barbaresi2018). The team dkosmajac used normalized Euclidean distance. After the shared task, the team Twist Bytes was able to slightly improve their F1-score by using a higher number of features (Benites et al. Reference Benites, Grubenmann, von Däniken, von Grünigen, Deriu and Cieliebak2018). However, the exact number of included features was not determined using the development set, but it was the optimal number for the test set. Using the full set of features resulted again in a lower score. We report the F1-scores obtained by the teams in Table 11 together with the results obtained in this article.
2.2 Language identification for Devanagari script
Language identification research in distinguishing between languages using the Devanagari script is much more uncommon than for the Latin script. However, some research was done already before the Indo-Aryan Language Identification shared task (ILI) at VarDial Reference Barbaresi2018 (Zampieri et al. Reference Jauhiainen, Lui, Zampieri, Baldwin and Lindén2018). Kruengkrai et al. (Reference Kruengkrai, Sornlertlamvanich and Isahara2006) presented results from language identification experiments between ten Indian languages, including four languages written in Devanagari: Sanskrit, Marathi, Magahi, and Hindi. For the ten Indian languages they obtained over 90% accuracy with 70-byte long mystery text sequences. As language identification method, they used SVMs with string kernels. Murthy and Kumar (Reference Murthy and Kumar2006) compared the use of LMs based on bytes with models based on aksharas. Aksharas are the syllables or orthographic units of the Brahmi scripts (Vaid and Gupta Reference Vaid and Gupta2002). After evaluating the language identification between different pairs of languages, they concluded that the akshara-based models perform better than byte-based. They used multiple linear regression as the classification method.
Sreejith, Indu, and Reghu Raj (Reference Sreejith, Indu and Reghu Raj2013) tested language identification with Markovian character and word n-grams from one to three with Hindi and Sanskrit. A character bigram-based language identifier fared the best and managed to gain an accuracy of 99.75% for sentence-sized mystery texts. Indhuja et al. (Reference Indhuja, Indu, Sreejith and Reghu Raj2014) continued the work of Sreejith et al. (Reference Sreejith, Indu and Reghu Raj2013) investigating the language identification between Hindi, Sanskrit, Marathi, Nepali, and Bhojpuri. In a similar fashion, they evaluated the use of Markovian character and word n-grams from one to three. For this set of languages, word unigrams performed the best, obtaining 88% accuracy with the sentence-sized mystery texts.
Bergsma et al. (Reference Bergsma, McNamee, Bagdouri, Fink and Wilson2012) collected tweets in three languages written with the Devanagari script: Hindi, Marathi, and Nepali. They managed to identify the language of the tweets with 96.2% accuracy using a logistic regression (LR) classifier (Hosmer, Lemeshow, and Sturdivant Reference Hosmer, Lemeshow and Sturdivant2013) with up to 4-grams of characters. Using an additional training corpus, they reached 97.9% accuracy with the A-variant of prediction by partial matching. Later, Pla and Hurtado (Reference Pla and Hurtado2017) experimented with the corpus of Bergsma et al. (Reference Bergsma, McNamee, Bagdouri, Fink and Wilson2012). Their approach using words weighted with TF-IDF and SVMs reached 97.7% accuracy on the tweets when using only the provided tweet training corpus. Hasimu and Silamu (Reference Hasimu and Silamu2018) included the same three languages in their test setting. They used a two-stage language identification system where the languages were first identified as a group using Unicode code ranges. In the second stage, the languages written with the Devanagari script were individually identified using SVMs with character bigrams. Their tests resulted in an F1-score of 0.993 within the group of languages using Devanagari with 700 best distinguishing bigrams. Indhuja et al. (Reference Indhuja, Indu, Sreejith and Reghu Raj2014) provided test results for several different combinations of the five languages, and for the set of languages used by Hasimu and Silamu (Reference Hasimu and Silamu2018), they reached 96% accuracy with word unigrams.
Rani et al. (2018) described a language identification system which they used for discriminating between Hindi and Magahi. Their language identifier using lexicons and suffixes of three characters obtained an accuracy of 86.34%. Kumar et al. (Reference Kumar, Lahiri, Alok, Ojha, Jain, Basit and Dawar2018) provided an overview of experiments on an earlier version of the dataset used in the ILI shared task including five closely related Indo-Aryan languages: Awadhi, Bhojpuri, Braj, Hindi, and Magahi. They managed to obtain an accuracy of 96.48% and a macro F1-score of 0.96 on the sentence level. For sentence level language identification, these results are quite good and as such they indicate that the languages, at least in their written form as evidenced by the corpus, are not as closely related as for example the Balkan languages: Croatian, Serbian, and Bosnian.
The results of the first shared task on Indo-Aryan language identification are described by Zampieri et al. (Reference Jauhiainen, Lui, Zampieri, Baldwin and Lindén2018). Eight teams submitted results on the task. Like in the second edition of the GDI shared task, we participated with an earlier version of the method described in this article. Again, our submission using a LM adaptation scheme reached a clear first place (Jauhiainen et al. Reference Jauhiainen, Jauhiainen and Lindén2018c). Seven other teams submitted results on the shared task. The team with the second-best results, Tübingen-Oslo, submitted their best results using SVMs (Çöltekin et al. Reference Çöltekin, Rama and Blaschke2018). In addition to the SVMs, they experimented with Recurrent Neural Networks (RNN) with GRUs and LSTMs, but their RNNs never achieved results comparable to the SVMs. The team ILIdentification used an SVM ensemble (Ciobanu et al. Reference Ciobanu, Zampieri, Malmasi, Pal and Dinu2018b). The best results for the team XAC were achieved using Ridge regression (Barbaresi Reference Barbaresi2018) in addition to which they experimented with NB and SGD classifiers. The team safina used CNNs with direct one-hot encoded vectors, with an embedding layer, as well as with a GRU layer (Ali Reference Ali2018b). The team dkosmajac used normalized Euclidean distance. The team we_are_indian used word-level LSTM RNNs in their best submission and statistical n-gram approach with mutual information in their second submission (Gupta et al. Reference Gupta, Dhakad, Gupta and Singh2018). The team LaMa used NB. We report the F1-scores obtained by the teams in Table 14 together with the results presented in this article.
2.3 LM adaptation
Even though LM adaptation has not been used in language identification of text in the past, it has been used in other areas of natural language processing. Jelinek et al. (Reference Jelinek, Merialdo, Roukos and Strauss1991) used a dynamic LM and Bacchiani and Roark (Reference Bacchiani and Roark2003) used self-adaptation on a test set in speech recognition. Bacchiani and Roark (Reference Bacchiani and Roark2003) experimented with iterative adaptation on their LMs and noticed that one iteration made the results better but that subsequent iterations made them worse. Zlatkova et al. (Reference Zlatkova, Kopev, Mitov, Atanasov, Hardalov, Koychev and Preslav2018) used a LR classifier in the Style Change Detection shared task (Kestemont et al. Reference Kestemont, Tschuggnall, Stamatatos, Daeleman, Specht, Stein and Potthast2018). Their winning system fitted their TF-IDF features on the testing data in addition to the training data.
LM adaptation was used by Chen and Liu (Reference Chen and Liu2005) for identifying the language of speech. In the system built by them, the speech is first run through Hidden Markov Model-based phone recognizers (one for each language) which tokenize the speech into sequences of phones. The probabilities of those sequences are calculated using corresponding LMs and the most probable language is selected. An adaptation routine is then used so that each of the phonetic transcriptions of the individual speech utterances is used to calculate probabilities for words , given a word n-gram history of h as in Equation (1).
where P o is the original probability calculated from the training material, P n the probability calculated from the data being identified, and P a the new adapted probability. λ is the weight given to original probabilities. This adaptation method resulted in decreasing the error rate in three-way identification between Chinese, English, and Russian by 2.88% and 3.84% on an out-of-domain (different channels) data and by 0.44% on in-domain (same channel) data.
Later, also Zhong et al. (Reference Zhong, Chen, Zhu and Liu2007) used LM adaptation in language identification of speech. They evaluated three different confidence measures and the best faring measure C is defined as follows:
where M is the sequence to be identified, n the number of frames in the utterance, g i the best identified language, and g j the second-best identified language. The two other evaluated confidence measures were clearly inferior. Although the C(g i, M) measure performed the best of the individual measures, a Bayesian classifier-based ensemble using all the three measures gave slightly higher results. Zhong et al. (Reference Zhong, Chen, Zhu and Liu2007) used the same language adaptation method as Chen and Liu (Reference Chen and Liu2005), using the confidence measures to set the λ for each utterance.
We used an earlier version of the LM adaptation technique presented in this article in three of the 2018 VarDial workshop shared tasks (Jauhiainen et al. Reference Jauhiainen, Jauhiainen and Lindén2018a; Reference Jauhiainen, Jauhiainen and Lindén2018b; Reference Jauhiainen, Jauhiainen and Lindén2018c).
The adaptive language identification method presented by Ionescu and Butnaru (Reference Ionescu and Butnaru2018) improved the accuracy from 76.27% to 78.35% on the ADI dataset. In their method, they retrain the LMs once by adding 1000 of the best identified (sorted by the confidence scores produced by their language identification method) unlabeled test samples to the training data.
3. The methods
In this section, we present the detailed descriptions of the methods used in the experiments. First, we describe HeLI 2.0, the language identification method used. Then we present the confidence measures we consider in this article. We conclude this section by describing the LM adaptation method used.
3.1 Language identification
We use the HeLI method (Jauhiainen et al. Reference Jauhiainen, Lindén and Jauhiainen2016) for language identification. The HeLI method has been rivalling SVMs already before the LM adaptation was added, reaching a shared first place in the 2016 Discriminating Similar Languages (DSL) shared task (Malmasi et al. Reference Malmasi, Zampieri, Ljubešić, Nakov, Ali and Tiedemann2016). The HeLI method is mostly non-discriminative,Footnote a and it is relatively quick to incorporate new material into the LMs of the language identifier. We have made a modification to the method where the original penalty value is replaced with a smoothing value that is calculated from the sizes of the LMs. This modification is needed especially for such cases where the LMs grow considerably because of LM adaptation, as the original penalty value was depending on the sizes of the training corpus during the development phase. The penalty modifier p mod is introduced to penalize those languages where features encountered during the identification are absent. The p mod parameter is optimized using the development corpus and in the experiments presented in this article, the optimal value varies between 1.09 and 1.16. The complete formula for the HeLI 2.0 method is presented here, and we provide the modified equations for the values used in the LMs in a similar notation as that used by Jauhiainen et al. (Reference Jauhiainen, Lindén and Jauhiainen2016).
The method aims to determine the language g ∈ G in which the mystery text M has been written, when all languages in the set G are known to the language identifier. Each language is represented by several different LMs only one of which is used for every word t found in the mystery text. The LMs for each language are one or more modelsFootnote b based on words and/or one or more models based on character n-grams from n min to n max. The mystery text is processed one word at a time. The word-based models are used first and if an unknown word is encountered in the mystery text, the method backs off to using the character n-grams of the size n max. If it is not possible to apply the character n-grams of the size n max, the method backs off to lower order character n-grams and, if needed, continues backing off until character n-grams of the size n min.
Creating the LMs: The training data can be preprocessed in different ways to produce different types of LMs. The most usual way is to lowercase the text and tokenize it into words using nonalphabetic and non-ideographic characters as delimiters. It is possible to generate several LMs for words using different preprocessing schemes, and then use the development material to determine which models and in which back-off order are usable for the current task.
The relative frequencies of the words are calculated. Also, the relative frequencies of character n-grams from 1 to n max are calculated inside the words, so that the preceding and the following space-characters are included.Footnote c The character n-grams are overlapping, so that for example a word with three characters includes three character trigrams. Word n-grams were not used in the experiments of this article, so all subsequent references to n-grams in this article refer to n-grams of characters. After calculating the relative frequencies, we transform those relative frequencies into scores using 10-based logarithms.
The corpus containing only the word tokens in the LMs is called C. A corpus C in language g is denoted by C g. dom(O(C)) is the set of all words found in the models of any of the languages g ∈ G. For each word t ∈ dom(O(C)), the values vCg (t) for each language g are calculated, as in Equation (3).
 $$v_{C_g } (t) = \left\{ {\begin{array}{*{20}c} { - \mathop {\log }\nolimits_{10} \left(\frac{{c(C_g ,t)}} {{l_{C_g } }}\right),} \hfill & {{\text{if}} c(C_g ,t) > 0} \hfill \\ { - \mathop {\log }\nolimits_{10} \left(\frac{1} {{l_{C_g } }}\right)p_{mod} ,} \hfill & {{\text{if}} c(C_g ,t) = 0} \hfill \\ \end{array} } \right.$$
$$v_{C_g } (t) = \left\{ {\begin{array}{*{20}c} { - \mathop {\log }\nolimits_{10} \left(\frac{{c(C_g ,t)}} {{l_{C_g } }}\right),} \hfill & {{\text{if}} c(C_g ,t) > 0} \hfill \\ { - \mathop {\log }\nolimits_{10} \left(\frac{1} {{l_{C_g } }}\right)p_{mod} ,} \hfill & {{\text{if}} c(C_g ,t) = 0} \hfill \\ \end{array} } \right.$$
where c(C g, t) is the number of words t and lCg is the total number of all words in language g. The parameter p mod is the penalty modifier which is determined empirically using the development set.
The corpus containing the n-grams of the size n in the LMs is called C n. The domain dom(O(C n)) is the set of all character n-grams of length n found in the models of any of the languages g ∈ G. The values ![]() $v_{\mathop C\nolimits_g^n } (u)$ are calculated in the same way for all n-grams u ∈ dom(O(C n)) for each language g, as shown in Equation (4).
$v_{\mathop C\nolimits_g^n } (u)$ are calculated in the same way for all n-grams u ∈ dom(O(C n)) for each language g, as shown in Equation (4).
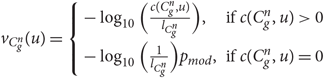 $$v_{C_g^n } (u) = \left\{ {\begin{array}{*{20}c} { - \mathop {\log }\nolimits_{10} \left(\frac{{c(C_g^n ,u)}} {{l_{C_g^n } }}\right),} \hfill & {{\text{if}} c(C_g^n ,u) > 0} \hfill \\ { - \mathop {\log }\nolimits_{10} \left(\frac{1} {{l_{C_g^n } }}\right)p_{mod} ,} \hfill & {{\text{if}} c(C_g^n ,u) = 0} \hfill \\ \end{array} } \right.$$
$$v_{C_g^n } (u) = \left\{ {\begin{array}{*{20}c} { - \mathop {\log }\nolimits_{10} \left(\frac{{c(C_g^n ,u)}} {{l_{C_g^n } }}\right),} \hfill & {{\text{if}} c(C_g^n ,u) > 0} \hfill \\ { - \mathop {\log }\nolimits_{10} \left(\frac{1} {{l_{C_g^n } }}\right)p_{mod} ,} \hfill & {{\text{if}} c(C_g^n ,u) = 0} \hfill \\ \end{array} } \right.$$
where ![]() $c(\mathop C\nolimits_g^n ,u)$ is the number of n-grams u found in the corpus of the language g and
$c(\mathop C\nolimits_g^n ,u)$ is the number of n-grams u found in the corpus of the language g and ![]() $l_{\mathop C\nolimits_g^n }$ is the total number of the n-grams of length n in the corpus of language g. These values are used when scoring the words while identifying the language of a text.
$l_{\mathop C\nolimits_g^n }$ is the total number of the n-grams of length n in the corpus of language g. These values are used when scoring the words while identifying the language of a text.
Scoring the text: The mystery text M is tokenized into words using the same tokenization scheme as when creating the LMs. The words are lowercased when lowercased models are being used. After this, a score v g(t) is calculated for each word t in the mystery text for each language g. If the word t is found in the set of words dom(O(C g)), the corresponding value vCg(t) for each language g is assigned as the score v g(t), as shown in Equation 5.
 $$v_g (t) = \left\{ {\begin{array}{*{20}c} {v_{C_g } (t),} \hfill & {\quad {\text {if}} t \in dom(O(C_g ))} \hfill \\ {v_g (t,min(n_{max} ,l_t + 2)),} \hfill & {\quad {\text {if}} t \notin dom(O(C_g ))} \hfill \\ \end{array} } \right.$$
$$v_g (t) = \left\{ {\begin{array}{*{20}c} {v_{C_g } (t),} \hfill & {\quad {\text {if}} t \in dom(O(C_g ))} \hfill \\ {v_g (t,min(n_{max} ,l_t + 2)),} \hfill & {\quad {\text {if}} t \notin dom(O(C_g ))} \hfill \\ \end{array} } \right.$$
If a word t is not found in the set of words dom(O(C g)) and the length of the word l t is at least n max − 2, the language identifier backs off to using character n-grams of the length n max. In case the word t is shorter than n max − 2 characters, n = l t + 2.
When using n-grams, the word t is split into overlapping n-grams of characters ![]() $u\matrix{n \cr i \cr } $ where i = 1, …, l t − n, of the length n. Each of the n-grams
$u\matrix{n \cr i \cr } $ where i = 1, …, l t − n, of the length n. Each of the n-grams ![]() $ u\matrix{ n \cr i \cr } $ is then scored separately for each language g in the same way as the words.
$ u\matrix{ n \cr i \cr } $ is then scored separately for each language g in the same way as the words.
If the n-gram ![]() $ u\matrix{ n \cr i \cr } $ is found in
$ u\matrix{ n \cr i \cr } $ is found in ![]() $ dom(O(C\matrix{ n \cr g \cr } )) $, the values in the models are used. If the n-gram
$ dom(O(C\matrix{ n \cr g \cr } )) $, the values in the models are used. If the n-gram ![]() $ u\matrix{ n \cr i \cr } $ is not found in any of the models, it is simply discarded. We define the function d g (t, n) for counting n-grams in t found in a model in Equation 6.
$ u\matrix{ n \cr i \cr } $ is not found in any of the models, it is simply discarded. We define the function d g (t, n) for counting n-grams in t found in a model in Equation 6.
 $$d_g (t,n) = \sum\limits_{i = 1}^{l_t - n} \left\{ {\begin{array}{*{20}c} {1,} \hfill & {\quad {\text{if}}u_i^n \in dom(O(C^n ))} \hfill \\ {0,} \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right.$$
$$d_g (t,n) = \sum\limits_{i = 1}^{l_t - n} \left\{ {\begin{array}{*{20}c} {1,} \hfill & {\quad {\text{if}}u_i^n \in dom(O(C^n ))} \hfill \\ {0,} \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right.$$
When all the n-grams of the size n in the word t have been processed, the word gets the value of the average of the scored n-grams ![]() $ u\matrix{ n \cr i \cr } $ for each language, as in Equation (7).
$ u\matrix{ n \cr i \cr } $ for each language, as in Equation (7).
 $$v_g (t,n) = \left\{ {\begin{array}{*{20}c} {\frac{1} {{d_g (t,n)}}\sum\nolimits_{i = 1}^{l_t - n} {v_{C_g^n } (u_i^n )} ,} \hfill & {{\text{if}}d_g (t,n) > 0} \hfill \\ {v_g (t,n - 1),} \hfill & {{\text{otherwise,}}} \hfill \\ \end{array} } \right.$$
$$v_g (t,n) = \left\{ {\begin{array}{*{20}c} {\frac{1} {{d_g (t,n)}}\sum\nolimits_{i = 1}^{l_t - n} {v_{C_g^n } (u_i^n )} ,} \hfill & {{\text{if}}d_g (t,n) > 0} \hfill \\ {v_g (t,n - 1),} \hfill & {{\text{otherwise,}}} \hfill \\ \end{array} } \right.$$
where d g (t, n) is the number of n-grams ![]() $ u\matrix{ n \cr i \cr } $ found in the domain
$ u\matrix{ n \cr i \cr } $ found in the domain ![]() $ dom(O(C\matrix{ n \cr g \cr } )) $. If all of the n-grams of the size n were discarded, d g (t, n) = 0, the language identifier backs off to using n-grams of the size n - 1.
$ dom(O(C\matrix{ n \cr g \cr } )) $. If all of the n-grams of the size n were discarded, d g (t, n) = 0, the language identifier backs off to using n-grams of the size n - 1.
The whole mystery text M gets the score R g (M) equal to the average of the scores of the words v g(t) for each language g, as in Equation (8).
 $$R_g (M) = \frac{{\sum\nolimits_{i = 1}^{l_{T(M)} } {v_g (t_i )} }} {{l_{T(M)} }}$$
$$R_g (M) = \frac{{\sum\nolimits_{i = 1}^{l_{T(M)} } {v_g (t_i )} }} {{l_{T(M)} }}$$
where T(M) is the sequence of words and l T(M) is the number of words in the mystery text M. Since we are using negative logarithms of probabilities, the language having the lowest score is returned as the language with the maximum probability for the mystery text.
3.2 Confidence estimation
In order to be able to select the best candidate for LM adaptation, the language identifier needs to provide a confidence score for the identified language. We evaluated three different confidence measures that seemed applicable to the HeLI 2.0 method.
In the first measure, we estimate the confidence of the identification as the difference between the scores R(M) of the best and the second best identified language. Zhong et al. (Reference Zhong, Chen, Zhu and Liu2007) call this confidence score CM BS, and in our case it is calculated using the following equation:
where g is the best scoring language and h the second best scoring language.
The second confidence measure, CM AVG, was presented by Chen and Liu (Reference Chen and Liu2005). In CM AVG, we calculate the difference between the score for the best identified language and the average of the scores of the rest of the languages. CM AVG adapted to our situation is calculated as follows:
 $$CM_{AVG} (M) = \frac{1} {{l_G - 1}}\sum\limits_{j = 1,j \ne g}^{l_G } R_j (M) - R_g (M)$$
$$CM_{AVG} (M) = \frac{1} {{l_G - 1}}\sum\limits_{j = 1,j \ne g}^{l_G } R_j (M) - R_g (M)$$
The third measure, CMPOST, presented by Zhong et al. (Reference Zhong, Chen, Zhu and Liu2007), is based on the posterior probability. We calculated it using the following equation:
 $$CM_{POST} (M) = \log \sum\limits_{j = 1}^{l_G } e^{R_j (M)} - R_g (M)$$
$$CM_{POST} (M) = \log \sum\limits_{j = 1}^{l_G } e^{R_j (M)} - R_g (M)$$
3.3 LM adaptation algorithm
In the first step of our adaptation algorithm, all the mystery texts M in the mystery text collection MC(e.g., a test set) are preliminarily identified using the HeLI 2.0 method. They are subsequently ranked by their confidence scores MC and the preliminarily identified collection is split into k − q parts MC 1…k. k is a number between 1 and the total number of mystery texts, l MC, depending on in how many parts we want to split the mystery text collection.Footnote d The higher k is, the longer the identification of the whole collection will take. The number of finally identified parts is q, which in the beginning is 0. After ranking, the part MC 1 includes the most confidently identified texts and MC k-q the least confidently identified texts.
Words and character n-grams up to the length n max are extracted from each mystery text in MC 1 and added to the respective LMs. Then, all the mystery texts in the part MC 1 are set as finally identified and q is increased by 1.
Then for as long as q < k, the process is repeated using the newly adapted LMs to perform a new preliminary identification for those texts that are not yet finally identified. In the end, all features from all of the mystery texts are included in the LM. This constitutes one epoch of adaptation.
In iterative LM adaptation, the previous algorithm is repeated from the beginning several times.
4. Test setting
We evaluate the methods presented in the previous section using three standard datasets. The first two datasets are from the GDI shared tasks held at VarDials 2017 and 2018. The third dataset is from the ILI shared task held at VarDial 2018.
4.1 GDI 2017 dataset
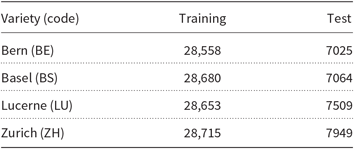
The dataset used in the GDI 2017 shared task consists of manual transcriptions of speech utterances by speakers from different areas in Switzerland: Bern, Basel, Lucerne, and Zurich. The variety of German spoken in Switzerland is considered to be a separate language (Swiss German, gsw) by the ISO-639-3 standard (Lewis, Simons, and Fennig Reference Lewis, Simons and Fennig2013), and these four areas correspond to separate varieties of it. The transcriptions in the dataset are written entirely in lowercased letters. Samardžić et al. (Reference Samardžić, Scherrer and Glaser2016) describe the ArchiMob corpus, which is the source for the shared task dataset. Zampieri et al. (Reference Malmasi and Zampieri2017) describe how the training and test sets were extracted from the ArchiMob corpus for the 2017 shared task. The sizes of the training and test sets can be seen in Table 1. The shared task was a four-way language identification task between the four German dialects present in the training set.
Table 1. List of the Swiss German varieties used in the datasets distributed for the 2017 GDI shared task. The sizes of the training and the test sets are in words
4.2 GDI 2018 dataset
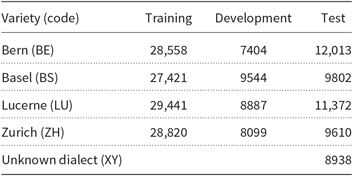
The dataset used in the GDI 2018 shared task was similar to the one used in GDI 2017. The sizes of the training, the development, and the test sets can be seen in Table 2. The first track of the shared task was a standard four-way language identification between the four German dialects present in the training set. The GDI 2018 shared task included an additional second track dedicated to unknown dialect detection. The unknown dialect was included neither in the training nor in the development sets, but it was present in the test set. The test set was identical for both tracks, but the lines containing an unknown dialect were ignored when calculating the results for the first track.
Table 2. List of the Swiss German varieties used in the datasets distributed for the 2018 GDI shared task. The sizes of the training, the development, and the test sets are in words
4.3 ILI 2018 dataset
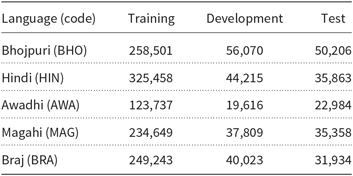
The dataset used for the ILI 2018 shared task included text in five languages: Bhojpuri, Hindi, Awadhi, Magahi, and Braj. The texts were mainly literature published over the web as well as in print. As can be seen in Table 3, there was considerably less training material for the Awadhi language than the other languages. The training corpus for Awadhi had only slightly over 9000 lines, whereas the other languages had around 15,000 lines of text for training. An earlier version of the dataset, as well as its creation, was described by Kumar et al. (Reference Kumar, Lahiri, Alok, Ojha, Jain, Basit and Dawar2018). The ILI 2018 shared task was an open one, allowing the use of any additional data or means. However, we have not used any external data, and our results would be exactly the same on a closed version of the task.
Table 3. List of the Indo-Aryan languages used in the datasets distributed for the 2018 ILI shared task. The sizes of the training, the development, and the test sets are in words
5. Experiments and results
In our experiments, we evaluate the HeLI 2.0 method, the HeLI 2.0 method using LM adaptation, as well as the iterative version of the adaptation. We test all three methods with all of the datasets described in the previous section. First we evaluate the confidence measures using the GDI 2017 dataset and afterwards we use the best performing confidence measure in all further experiments.
We are measuring language identification performance using the macro and the weighted F1-scores. These are the same performance measures that were used in the GDI 2017, GDI 2018, and ILI 2018 shared tasks (Zampieri et al. Reference Malmasi and Zampieri2017; Reference Jauhiainen, Lui, Zampieri, Baldwin and Lindén2018). F1-score is calculated using the precision and the recall as in Equation (12).
The macro F1-score is the average of the individual F1-scores for the languages and the weighted F1-score is similar but weighted by the number of instances for each language.
5.1 Evaluating the confidence measures
We evaluated the three confidence measures presented in Section 3.2 using the GDI 2017 training data. The results of the evaluation are presented in Table 4. The underlying data for the table consists of pairs of confidence values and the corresponding Boolean values indicating whether the identification results were correct or not. The data have been ordered according to their confidence score for each of the three measures. The first column in the table tells the percentage of examined top scores. The other columns give the average accuracy in that examined portion of identification results for each confidence measure.
Table 4. Average accuracies within the 10% portions when the results are sorted by the confidence scores CM
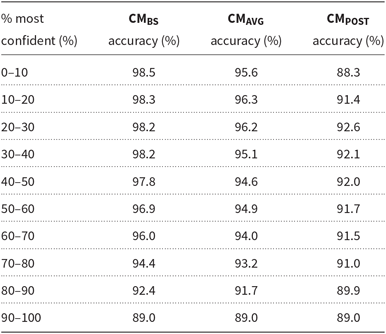
The first row tells us that in the 10% of the highest confidence identification results according to the CM BS-measure, 98.5% of the performed identifications were correct. The two other confidence measures on the other hand fail to arrange the identification results so that the most confident 10% would be the most accurate 10%. As a whole, this experiment tells us that the CM BS-measure is stable and performs well when compared with the other two.
In addition to evaluating each individual confidence measure, Zhong et al. (Reference Zhong, Chen, Zhu and Liu2007) evaluated an ensemble combining all of the three measures, gaining somewhat better results than with the otherwise best performing CM BS-measure. However, in their experiments the two other measures were much more stable than in ours. We decided to use only the simple and well-performing CM BS-measure with our LM adaptation algorithm in the following experiments.
5.2 Experiments on the GDI 2017 dataset
5.2.1 Baseline results and parameter estimation
As there was no separate development set provided for the GDI 2017 shared task, we divided the training set into training and development partitions. The last 500 lines from the original training data for each language was used for development. The development partition was then used to find the best parameters for the HeLI 2.0 method using the macro F1-score as the performance measure. The macro F1-score is equal to the weighted F1-score, which was used as a ranking measure in the shared task, when the number of tested instances in each class are equal. On the development set, the best macro F1-score of 0.890 was reached with the language identifier where n max = 5 words being used and p mod = 1.16. We then used the whole training set to train the LMs. On the test set, the language identifier using the same parameters reached the macro F1-score of 0.659 and the weighted F1-score of 0.639.
5.2.2 Experiments with LM adaptation
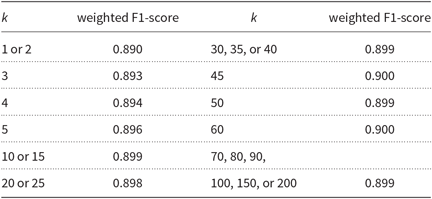
First, we determined the best value for the number of splits k using the development partition. Table 5 shows the increment of the weighted F1-score with different values of k on the development partition using the same parameters with the HeLI 2.0 method as for the baseline. The results with k = 1 are always equal to the baseline. If k is very high, the identification becomes computationally costly as the number of identifications grows exponentially in proportion to k. The absolute increase of the F1-score on the development partition was 0.01 when using k = 45.
Table 5. The weighted F1-scores obtained by the identifier using LM adaptation with different values of k when tested on the development partition of the GDI 2017 dataset
5.2.3 Experiments with thresholding
We experimented with setting a confidence threshold for the inclusion of new data into the LMs. Table 6 shows the results on the development partition. The results show that there is no confidence score that could be used for thresholding, at least not with the development partition of GDI 2017.
Table 6. Weighted F1-scores with confidence threshold for LM adaptation on the development set

5.2.4 Results of the LM adaptation on the test data
Based on the evaluations using the development partition, we decided to use k = 45 for the test run. All the training data were used for the initial LM creation. The language identifier using LM adaptation reached the macro F1-score of 0.689 and the weighted F1-score of 0.687 on the test set. The weighted F1-score was 0.048 higher than the one obtained by the nonadaptive version and clearly higher than the other results obtained using the GDI 2017 dataset.
5.2.5 Iterative adaptation
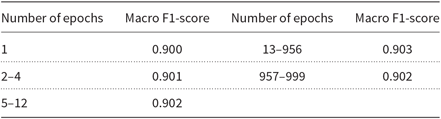
We tested repeating the LM adaptation algorithm for several epochs, and the results of those trials on the development partition can be seen in Table 7. The improvement of 0.003 on the original macro F1-score using 13–956 epochs was still considerable. The results seem to indicate that the LMs become very stable with repeated adaptation.
Table 7. Macro F1-scores with iterative LM adaptation on the development partition
We decided to try iterative LM adaptation using 485 epochs with the test set. The tests resulted in a weighted F1-score of 0.700, which was a further 0.013 increase on top of the score obtained without additional iterations. We report the weighted F1-scores from the GDI 2017 shared task together with our own results in Table 8. The methods used are listed in the first column, used features in the second column, and the best reached weighted F1-score in the third column. The results from this paper are bolded. The results using other methods (team names are in parentheses) are collected from the shared task report (Zampieri et al. Reference Malmasi and Zampieri2017) as well as from the individual system description articles. The 0.013 point increase obtained with the iterative LM adaptation over the non-iterative version might seem small when compared with the overall increase over the scores of the HeLI 2.0 method, but the increase is still more than the difference between the first and third best submitted methods on the original shared task.
Table 8. The weighted F1-scores using different methods on the 2017 GDI test set. The results from the experiments presented in this article are bolded. The system description papers of each team, if existing, are listed in Section 2.1

5.3 Experiments on the GDI 2018 dataset
5.3.1 Baseline results and parameter estimation
The GDI 2018 dataset included a separate development set (Table 2). We used the development set to find the best parameters for the HeLI 2.0 method using the macro F1-score as the performance measure. The macro F1-score of 0.659 was obtained by the HeLI 2.0 method using just character n-grams of the size 4 with p mod = 1.15. The corresponding recall 66.17% was slightly higher than the 66.10% obtained with the HeLI method used in the GDI 2018 shared task. We then used the combined training and the development sets to train the LMs. On the test set, the language identifier using these parameters obtained a macro F1-score of 0.650. The HeLI 2.0 method reached 0.011 higher macro F1-score than the HeLI method we used in the shared task. Even without the LM adaptation, the HeLI 2.0 method beats all the other reported methods.
5.3.2 Experiments with LM adaptation
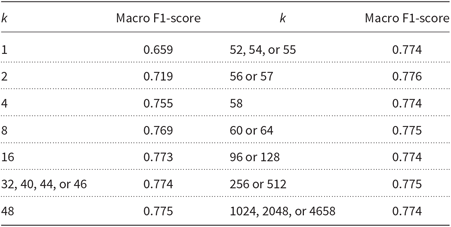
Table 9 shows the increment of the macro F1-score with different values of k, the number of parts the examined mystery text collection is split into, on the development set using the same parameters with the HeLI 2.0 method as for the baseline. On the development set, k = 57 gave the best F1-score, with the absolute increase of 0.116 over the baseline. The corresponding recall was 77.74%, which was somewhat lower than the 77.99% obtained at the shared task.
Table 9. The macro F1-scores gained with different values of k when evaluated on the GDI 2018 development set
5.3.3 Results of the LM adaptation on the test set
Based on the evaluations using the development set, we decided to use k = 57 for the test run. All the training and the development data were used for the initial LM creation. The method using the LM adaptation algorithm reached the macro F1-score of 0.707. This macro F1-score is 0.057 higher than the one obtained by the nonadaptive version and 0.021 higher than the results we obtained using LM adaptation in the GDI 2018 shared task. The performance improvement with LM adaptation is partly due to the ability of the HeLI 2.0 to better handle the adapted LMs and the optimization of the k-value.
5.3.4 Iterative adaptation
We tested repeating the LM adaptation algorithm for several epochs, and the results of those trials on the GDI 2018 development set can be seen in Table 10. There was a clear improvement of 0.041, at 477–999 epochs, on the original macro F1-score. It would again seem that the LMs become very stable with repeated adaptation, at least when there is no unknown language present in the data which is the case with the development set. Good scores were obtained already at 20 iterations, after which the results started to fluctuate up and down.
Table 10. Macro F1-scores with iterative LM adaptation on the GDI 2018 development set

Based on the results on the development set, we decided to try two different counts of iterations: 738, which is the number of epochs in the middle of the best scores, and 20, after which the results started to fluctuate. The tests resulted in a macro F1-score of 0.696 with 738 epochs and 0.704 with 20 epochs. As an additional experiment, we evaluated the iterative adaptation on a test set, from which the unknown dialects had been removed and obtained an F1-score of 0.729 with 738 epochs. From the results, it is clear that the presence of the unknown language is detrimental to repeated LM adaptation. In Table 11, we report the macro F1-scores obtained by the teams participating in the GDI 2018 shared task, as well as our own. The methods used are listed in the first column, used features in the second column, and the best reached macro F1-score in the third column.
Table 11. The macro F1-scores using different methods on the 2018 GDI test set. The results from the experiments presented in this article are bolded. The system description papers of each team, if existing, are listed in Section 2.1

5.4 Experiments on the ILI 2018 dataset
5.4.1 Baseline results and parameter estimation
We used the development set to find the best parameters for the HeLI 2.0 method using the macro F1-score as the measure. Using both original and lowercased character n-grams from one to six with p mod = 1.09, the method obtained the macro F1-score of 0.954. The corresponding recall was 95.26%, which was exactly the same we obtained with the HeLI method used in the ILI 2018 shared task. We then used the combined training and the development sets to train the LMs. On the test set, the language identifier using the above parameters obtained a macro F1-score of 0.880, which was clearly lower than the score we obtained using the HeLI method in the shared task.
5.4.2 Experiments with LM adaptation
Table 12 shows the increment of the macro F1-score with different values of on the development set using the same parameters with the HeLI 2.0 method as for the baseline. On the development set, k= 64 gave the best F1-score, 0.964, which is an absolute increase of 0.010 on the original F1-score. The corresponding recall was 96.29%, which was a bit better than the 96.22% obtained in the shared task.
Table 12. The macro F1-scores gained with different values of k when tested on the ILI 2018 development set

5.4.3 Results of the LM adaptation on the test data
Based on the evaluations using the development data, we decided to use k = 64 as the number of splits for the actual test run. All the training and the development data were used for the initial LM creation. The identifier using the LM adaptation algorithm obtained a macro F1-score of 0.955. This macro F1-score is basically the same we obtained with LM adaptation in the ILI 2018 shared task, only some small fractions lower.
5.4.4 Iterative adaptation
We experimented repeating the LM adaptation algorithm for several epochs, and the results of those trials on the development set can be seen in Table 13. There was a very small improvement of 0.001 on the original macro F1-score. The best absolute F-scores were reached at epochs 17 and 18. It would again seem that the LMs become very stable with repeated adaptation.
Table 13. Macro F1-scores with iterative LM adaptation on the ILI 2018 development set

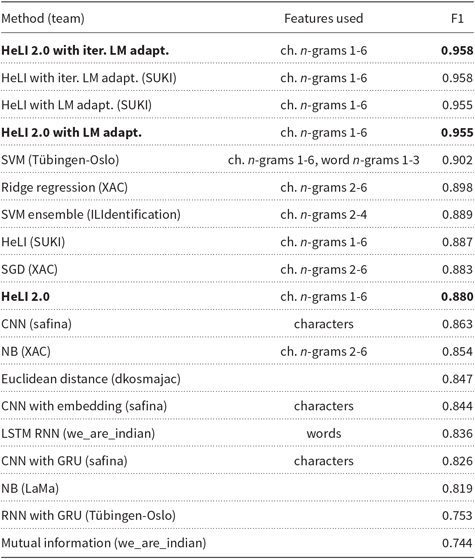
Based on the results on the development set, we decided to use LM adaptation with 18 iterations on the test set. The test resulted in a macro F1-score of 0.958, which is again almost the same as in the shared task, though this time some small fractions higher. We report the F1-scores obtained by the different teams participating in the ILI 2018 shared task in Table 14, with the results from this article in bold. The methods used are listed in the first column, used features in the second column, and the macro F1-scores in the third column.
Table 14. The macro F1-scores using different methods on the 2018 ILI test set. The results presented for the first time are in bold. The system description papers of each team, if existing, are listed in Section 2.2
6. Discussion
The LM adaptation scheme proved to be of great importance with all three datasets. The F1-scores improved from 5 to 7 absolute points from the results gained by the same methods without LM adaptation. The fundamental component for the performance improvement is the ability to learn new information from the test set itself. As of this writing, the results from the shared tasks of VarDial 2019 (Zampieri et al. Reference Zampieri, Malmasi, Scherrer, Samardžić, Tyers, Silfverberg, Klyueva, Pan, Huang, Ionescu, Butnaru and Jauhiainen2019) are being prepared for publication, and several participating teams had incorporated some sort of an LM adaptation algorithm into their systems. We used the same LM adaptation scheme as presented in this paper with the HeLI 2.0 method as well as with a custom NB implementation (Jauhiainen, Jauhiainen, and Lindén Reference Jauhiainen, Jauhiainen and Lindén2019), two teams used such a scheme with SVMs (Benites, von Däniken, and Cieliebak Reference Benites, Däniken and Cieliebak2019; Wu et al. Reference Wu, DeMattos, So, Chen and Çöltekin2019) and one learned new information from the test set with deep neural networks (Bernier-Colborne, Goutte, and Léger Reference Bernier-Colborne, Goutte and Léger2019). All three shared tasksFootnote e concentrating on language, dialect, or variety identification were won using one of these systems.
The results using the HeLI 2.0 method and the improved LM adaptation are clearly better with the GDI 2018 dataset than the ones with the original HeLI method. However, with the ILI 2018 dataset, there is no real difference in performance between the old and the new methods. This is at least partly due to the fact that the size of the test set relative to the training set is much larger with the GDI 2018 dataset than with the ILI 2018 dataset.
The additional performance gained using the LM adaptation on the GDI 2017 development data (F1-score rose from 0.890 to 0.903) was much less than in the GDI 2018 development data (F1-score rose from 0.659 to 0.817). This indicates that the training and the development data of the GDI 2017 were already in-domain with each other as opposed to being out-of-domain in the GDI 2018 data. Additionally, the 26% difference in F1-scores between the development portion (0.890) and the test set (0.659) of the GDI 2017 data obtained by the HeLI 2.0 method is considerable. It seems to indicate that the test set contains more out-of-domain material when compared with the partition of the training set we used for development. In order to validate this hypothesis, we divided the test set into two parts. The second part remained to be used for testing in four scenarios with the HeLI 2.0 method. In the scenarios we used different combinations of data for training: the original training set, the training set augmented with the first part of test data, the training set of which a part was replaced by the first part of the test set, and only using the first part of the test set. The results of these experiments support our hypothesis, as can be seen in Table 15. The domain difference between the two sets explains why iterative adaptation performs better with the test set than with the development set. After each iteration, the relative amount of the original training data gets smaller, as the information from the test data is repeatedly added to the LMs.
Table 15. The macro F1-scores for the second part of test set using different training data combinations

In the GDI 2018 dataset, there is only a 1.4% difference between the macro F1-scores obtained from the development and the test sets. This indicates that the GDI 2018 development set is in the same way out-of-domain when compared with the training set as the actual test set is.
There is a small difference (7.8%) between the F1-scores attained using the development set and the test set of the ILI 2018 data as well. However, such small differences can be partly due to the fact that the parameters of the identification method have been optimized using the development set.
Though the iterative LM adaptation is computationally costly when compared with the baseline HeLI 2.0 method, it must be noted that the final identifications with 485 epochs on the GDI 2017 test set took only around 20 minutes using one computing core of a modern laptop. We provide the time taken for creating the initial LMs for each dataset as well as the time taken by different methods when calculating the predictions on the test partitions of the different datasets in Table 16.Footnote f
Table 16. Time measurements for creating the LMs and predicting the language for different test sets. The measurements give some indication of the computational efficiency but can only be considered rough estimates

The time taken by the iterative LM-adaptation is linearly related to the number of epochs used. With the GDI 2017 dataset, one epoch took around 2.45 seconds, which is also near the difference between the basic HeLI 2.0 method and the one with LM adaptation. The reason for one round of LM adaptation taking so much longer (7.64 seconds) with the GDI 2018 test set is that the number of splits used also adds linearly to the time consumed. The test sets were also considerably different in size, and the size of the test set also linearly affects the time used. The ILI 2018 test set had around five times more sentences than that of GDI 2017.
We are not providing an error analysis of the errors made by our system on the test sets. If we would do so, it would make us, and any of the readers, less qualified to use these same datasets for further development of our methods.
7. Conclusions
The results indicate that unsupervised LM adaptation should be considered in all language identification tasks, especially in those where the amount of out-of-domain data is significant. If the presence of unseen languages is to be expected, the use of LM adaptation could still be beneficial, but special care must be taken as repeated adaptation in particular could decrease the identification accuracy. We were delighted to see that some of the other participants of the 2019 VarDial Evaluation Campaign (Zampieri et al. Reference Zampieri, Malmasi, Scherrer, Samardžić, Tyers, Silfverberg, Klyueva, Pan, Huang, Ionescu, Butnaru and Jauhiainen2019) had noticed our LM adaptation scheme and used a somewhat similar way of gathering new information from the test sets with their own systems.
8. Future work
We believe that it is possible to apply a similar adaptation scheme with other NLP problems and especially with other classification tasks. We are looking forward to investigating these possibilities in the future.
An experiment left for future work is to test how the amount of test data affects the final language identification accuracy. In the experiment, we would divide the test sets into smaller parts and evaluate how the LM adaptation technique performs in them. Our intuition suggests that the smaller the test set, the less effective the LM adaptation will be. However, if the larger test set consists of texts in several separable domains, it might actually be beneficial to divide the test set to smaller parts.
The adaptation technique presented in this paper could, in theory, be used to annotate a large dataset with an extremely small training set, maybe even with just one sentence. This is perhaps the most interesting avenue for further research.
Acknowledgements
This research was partly conducted with funding from the Kone Foundation Language Programme (Kone Foundation 2012) and from FIN-CLARIN. We thank the anonymous reviewers for their thought-provoking questions.

















