Article contents
Toward random walk-based clustering of variable-order networks
Published online by Cambridge University Press: 22 December 2022
Abstract
Higher-order networks aim at improving the classical network representation of trajectories data as memory-less order 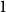 $1$ Markov models. To do so, locations are associated with different representations or “memory nodes” representing indirect dependencies between visited places as direct relations. One promising area of investigation in this context is variable-order network models as it was suggested by Xu et al. that random walk-based mining tools can be directly applied on such networks. In this paper, we focus on clustering algorithms and show that doing so leads to biases due to the number of nodes representing each location. To address them, we introduce a representation aggregation algorithm that produces smaller yet still accurate network models of the input sequences. We empirically compare the clustering found with multiple network representations of real-world mobility datasets. As our model is limited to a maximum order of
$1$ Markov models. To do so, locations are associated with different representations or “memory nodes” representing indirect dependencies between visited places as direct relations. One promising area of investigation in this context is variable-order network models as it was suggested by Xu et al. that random walk-based mining tools can be directly applied on such networks. In this paper, we focus on clustering algorithms and show that doing so leads to biases due to the number of nodes representing each location. To address them, we introduce a representation aggregation algorithm that produces smaller yet still accurate network models of the input sequences. We empirically compare the clustering found with multiple network representations of real-world mobility datasets. As our model is limited to a maximum order of 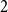 $2$, we discuss further generalizations of our method to higher orders.
$2$, we discuss further generalizations of our method to higher orders.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
Footnotes
Action Editor: Ulrik Brandes
References
- 1
- Cited by

