Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T10:40:40.781Z Has data issue: false hasContentIssue false
  • English
  • Français

Toward random walk-based clustering of variable-order networks

Published online by Cambridge University Press:  22 December 2022

Julie Queiros ,
Célestin Coquidé  and
François Queyroi Open the ORCID record for François Queyroi [Opens in a new window]
Julie Queiros*
Affiliation:
Nantes Université, Ecole Centrale Nantes, CNRS, LS2N, UMR 6004, F-44000, Nantes, France
Célestin Coquidé
Affiliation:
Nantes Université, Ecole Centrale Nantes, CNRS, LS2N, UMR 6004, F-44000, Nantes, France
François Queyroi
Affiliation:
Nantes Université, Ecole Centrale Nantes, CNRS, LS2N, UMR 6004, F-44000, Nantes, France
*
*Corresponding author. Email: julie.queiros@univ-nantes.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Higher-order networks aim at improving the classical network representation of trajectories data as memory-less order 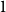$1$ Markov models. To do so, locations are associated with different representations or “memory nodes” representing indirect dependencies between visited places as direct relations. One promising area of investigation in this context is variable-order network models as it was suggested by Xu et al. that random walk-based mining tools can be directly applied on such networks. In this paper, we focus on clustering algorithms and show that doing so leads to biases due to the number of nodes representing each location. To address them, we introduce a representation aggregation algorithm that produces smaller yet still accurate network models of the input sequences. We empirically compare the clustering found with multiple network representations of real-world mobility datasets. As our model is limited to a maximum order of 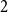$2$ , we discuss further generalizations of our method to higher orders.

Keywords

network analysishigher-order networksclusteringrandom walksequential data
Type
Research Article
Information
Network Science , Volume 10 , Issue 4 , December 2022 , pp. 381 - 399
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Action Editor: Ulrik Brandes

References

Battiston, F., Cencetti, G., Iacopini, I., Latora, V., Lucas, M., Patania, A. … Petri, G. (2020). Networks beyond pairwise interactions: structure and dynamics. Physics Reports, 874, 1–92.CrossRefGoogle Scholar
Begleiter, R., El-Yaniv, R., & Yona, G. (2004). On prediction using variable order Markov models. Journal of Artificial Intelligence Research, 22, 385–421.CrossRefGoogle Scholar
Brin, S., & Page, L. (1998). The anatomy of a large-scale hypertextual web search engine. Computer Networks and ISDN Systems, 30(1-7), 107–117.CrossRefGoogle Scholar
Chen, R., Sun, H., Chen, L., Zhang, J., & Wang, S. (2021). Dynamic order Markov model for categorical sequence clustering. Journal of Big Data, 8(1), 1–25.CrossRefGoogle ScholarPubMed
Ching, W. K., Fung, E. S., & Ng, M. K. (2004). Higherorder Markov chain models for categorical data sequences. Naval Research Logistics (NRL), 51(4), 557–574.CrossRefGoogle Scholar
Coquidé, C., Queiros, J., & Queyroi, F. (2021). PageRank computation for Higher-Order networks. In International Conference on Complex Networks and Their Applications (pp. 183–193). Cham: Springer.Google Scholar
Dao, V. L., Bothorel, C., & Lenca, P. (2020). Community structure: a comparative evaluation of community detection methods. In Network Science, Vol. 8, (pp. 1–41). Cambridge University Press.Google Scholar
Eliassi-Rad, T., Latora, V., Rosvall, M., Scholtes, I., & Dokumente, G. (2021). Higher-Order graph models: From theoretical foundations to machine learning. Dagstuhl Reports, Dagstuhl Seminar 21352.Google Scholar
Jääskinen, V., Xiong, J., Corander, J., & Koski, T. (2014). Sparse Markov chains for sequence data. Scandinavian Journal of Statistics, 41(3), 639–655.CrossRefGoogle Scholar
Krieg, S. J., Kogge, P. M., & Chawla, N. V. (2020). GrowHON: a scalable algorithm for growing Higher-order networks of sequences. In International Conference on Complex Networks and Their Applications (pp. 485–496). Cham: Springer.Google Scholar
Lambiotte, R., Rosvall, M., & Scholtes, I. (2019). From networks to optimal higher-order models of complex systems. Nature Physics, 15(4), 313–320.CrossRefGoogle ScholarPubMed
Lancichinetti, A., Fortunato, S., & Radicchi, F. (2008). Benchmark graphs for testing community detection algorithms. Physical Review E, 78(4), 046110.CrossRefGoogle ScholarPubMed
Manning, C. D., Raghavan, P., & Schütze, H. (2008). Hierarchical clustering (pp. 346–368). Cambridge University Press.Google Scholar
McDaid, A. F., Greene, D., & Hurley, N. (2011). Normalized mutual information to evaluate overlapping community finding algorithms, arXiv preprint arXiv: 1110.2515.Google Scholar
Pons, P., & Latapy, M. (2006). Computing communities in large networks using random walks. Journal of Graph Algorithms and Applications, 10(2), 191–218.CrossRefGoogle Scholar
Ron, D., y., S., & Tishby, N. (1994). Learning probabilistic automata with variable memory length. In Proceedings of the seventh annual conference on Computational learning theory (COLT ’94) (pp. 35–46). New York, NY, USA: Association for Computing Machinery.CrossRefGoogle Scholar
Rosvall, M., Axelsson, D., & Bergstrom, C. T. (2009). The map equation. In The European physical journal special topics, Vol. 178, (pp. 13–23). Springer.Google Scholar
Rosvall, M., Esquivel, A. V., Lancichinetti, A., West, J. D., & Lambiotte, R. (2014). Memory in network flows and its effects on spreading dynamics and community detection. Nature Communications, 5(1), 1–13.CrossRefGoogle ScholarPubMed
Saebi, M., Xu, J., Grey, E., Lodge, D., Corbett, J., & Chawla, N. V. (2020). Higher-order patterns of aquatic species spread through the global shipping network. PLOS ONE, 15(7), e0220353.CrossRefGoogle ScholarPubMed
Saebi, M., Xu, J., Kaplan, L. M., Ribeiro, B., & Chawla, N. V. (2020). Efficient modeling of higher-order dependencies in networks: from algorithm to application for anomaly detection. EPJ Data Science, 9(1), 15.CrossRefGoogle Scholar
Scholtes, I. (2017). When is a network a network? Multi-order graphical model selection in pathways and temporal networks. In Proceedings of the 23rd ACM SIGKDD international conference on knowledge discovery and data mining (pp. 1037–1046).Google Scholar
Torres, L., Blevins, A. S., Bassett, D., & Eliassi-Rad, T. (2021). The why, how, and when of representations for complex systems. SIAM Review, 63(3), 435–485.CrossRefGoogle Scholar
Xie, J., Kelley, S., & Szymanski, B. K. (2013). Overlapping community detection in networks: The state-of-the-art and comparative study. Acm Computing Surveys (CSUR), 45(4), 1–35.CrossRefGoogle Scholar
Xu, J., Wickramarathne, T. L., & Chawla, N. V. (2016). Representing higher-order dependencies in networks. Science Advances, 2(5), e1600028.CrossRefGoogle ScholarPubMed