Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T20:13:16.476Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Approximation of the Derivatives of Spline Quasi-Interpolation in Cubic Spline Space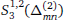

Published online by Cambridge University Press:  28 May 2015

Jiang Qian  and
Fan Wang
Jiang Qian*
Affiliation:
College of Sciences, Hohai University, Nanjing 210098, China Center for Numerical Simulation Software in Engineering and Sciences, Department of Engineering Mechanics, Hohai University, Nanjing 210098, China
Fan Wang
Affiliation:
College of Engineering, Nanjing Agricultural University, Nanjing 210031, China
*
Corresponding author.Email address:qianjianghhu@sina.com
Get access

Abstract

In this paper, based on the basis composed of two sets of splines with distinct local supports, cubic spline quasi-interpolating operators are reviewed on nonuniform type-2 triangulation. The variation diminishing operator is defined by discrete linear functionals based on a fixed number of triangular mesh-points, which can reproduce any polynomial of nearly best degrees. And by means of the modulus of continuity, the estimation of the operator approximating a real sufficiently smooth function is reviewed as well. Moreover, the derivatives of the nearly optimal variation diminishing operator can approximate that of the real sufficiently smooth function uniformly over quasi-uniform type-2 triangulation. And then the convergence results are worked out.

Keywords

65D0741A25Bivariate splinesconformality of smoothing cofactor methodnonuniform type-2 triangulationquasi-interpolationmodulus of continuity
Type
Research Article
Information
Numerical Mathematics: Theory, Methods and Applications , Volume 7 , Issue 1 , February 2014 , pp. 1 - 22
Copyright
Copyright © Global Science Press Limited 2014

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Dagnino, C. and Lamberti, P., On the approximation power of bivariate quadratic C1 splines, J. Comput. Appl. Math., 131 (2001), pp. 321–332.Google Scholar
[2] Dagnino, C. and Lamberti, P., Some performances of local bivariate quadratic C1 quasi-interpolating splines on nonuniform type-2 triangulations, J. Comput. Appl. Math., 173 (2005), pp. 21–37.Google Scholar
[3] Farin, G., Curves and Surfaces for Computer Aided Geometric Design, A Practical Guide, Academic Press, Boston, 1992.Google Scholar
[4] Li, C. J. and Chen, J., On the dimensions ofbivariate spline spaces and their stability, J. Comput. Appl. Math., 236 (2011), pp. 765–774.Google Scholar
[5] Li, C. J. and Wang, R. H., Bivariate cubic spline space and bivariate cubic NURBS surfaces, Proceedings of Geometric Modeling and Processing 2004, IEEE Computer Society Pressvol, pp. 115–123.Google Scholar
[6] Liu, H. W., Hong, D. and Cao, D. Q., Bivariate C1 cubic spline space over a nonuniform type-2 triangulation and its subspaces with boundary conditions, J. Comput. Math. Appl., 49 (2005), pp. 1853–1865.CrossRefGoogle Scholar
[7] Piegl, L. and Tiller, W., The NURBS Book, Spring-Verlag, Berlin, 1997.Google Scholar
[8] Qian, J. and Liu, H. Y., Relationship between UAH B splines and uniform B splines, J. Hohai Univ., (Natural Sciences), 34(5) (2006), pp. 599–602.Google Scholar
[9] Qian, J. and Tang, Y. H., On non-uniform Algebraic-Hyperbolic (NUAH) B-splines, Numer. Math. A Journal of Chinese Universities, 15(4) (2006), pp. 320–335.Google Scholar
[10] Qian, J. and Y Tang, H., The application of H Bezier-like curves in engineering, J. Numer. Methods Comput. Appl., 28(3) (2007), pp. 167–178.Google Scholar
[11] Ian, J.Q., Ang, R.H.W. and C.J.Li, , The bases of non-uniform cubic spline space , Numer. Math. Theor. Meth. Appl., 5(4) (2012), pp. 635–652.Google Scholar
[12] Qian, J., Wang, R. H., Zhu, C. G. and Wang, F., On spline quasi-interpolation in cubic spline space , Submitted.Google Scholar
[13] Schumaker, L. L., On the dimension of spaces of piecewise polynomials in two variables, Multi-variate Approximation Theory, Schempp, W and Zeller, K. (Eds.), Birkhauser, Basel, 1979, pp. 396–412.CrossRefGoogle Scholar
[14] Schumaker, L. L., Spline Functions: Basic Theory, Krieger Publishing Company, Malabar FL, 1993.Google Scholar
[15] Wang, G. Z., Chen, Q. Y. and Zhou, M. H., NUATB-spline Curves, Comput. Aided Geom. Design, 21(2004), pp. 193–205.CrossRefGoogle Scholar
[16] Wang, G.J., Wang, G. Z. and Zheng, J. M., Computer Aided Geometric Design, China Higher Education Press/Spring-Verlag Berlin, Beijing/Heidelberg, 2001.Google Scholar
[17] Wang, R. H., The structural characterization and interpolation for multivariate splines, Acta Math. Sinica, 18 (1975), pp. 91–106.Google Scholar
[18] Wang, R. H., Shi, X. Q., Luo, Z. X. and Su, Z. X., Multivariate Spline Functions and Their Applications, Science Press/Kluwer Academic Publishers, Beijing, New York, Dordrecht, Boston, London, 2001.CrossRefGoogle Scholar
[19] Wang, R. H. and Li, C. J., Bivariate quartic spline spaces and quasi-interpolation operators, J. Comput. Appl. Math., 190 (2006), pp. 325–338.CrossRefGoogle Scholar
[20] Wang, R. H. and Y LU, Quasi-interpolating operators and their applications in hypersingular integrals, J. Comput. Math., 16(4) (1998), pp. 337–344.Google Scholar
[21] Wang, R. H. and Lu, Y, Quasi-interpolating operators in on non-uniform type-2 triangulations, Numer. Math. A Journal of Chinese Universities, 2 (1999), pp. 97–103.Google Scholar
[22] Wang, S. M., Spline interpolation over type-2 triangulations, Appl. Math. Comput., 49 (1992), pp. 299–313.Google Scholar
[23] Wang, S. M. and Wang, C. L., Smooth interpolation on some triangulations, Utilitas Math., 41 (1992), pp. 309–317.Google Scholar
[24] Xu, Z. Q. and Wang, R. H., The instability degree in the dimension of spaces of bivariate spline, Approx. Theory Appl., 18(1) (2002), pp. 68–80.Google Scholar