Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T16:09:45.574Z Has data issue: false hasContentIssue false
  • English
  • Français

Efficient Convex Optimization Approaches to Variational Image Fusion

Published online by Cambridge University Press:  28 May 2015

Jing Yuan ,
Brandon Miles ,
Greg Garvin ,
Xue-Cheng Tai  and
Aaron Fenster
Jing Yuan*
Affiliation:
Medical Imaging Lab, Robarts Research Institute, University of Western Ontario, London ON, Canada N6A 5B7
Brandon Miles*
Affiliation:
Medical Imaging Lab, Robarts Research Institute, University of Western Ontario, London ON, Canada N6A 5B7
Greg Garvin*
Affiliation:
Department of Medical Imaging, St Jospeh’s HealthCare, London ON, Canada
Xue-Cheng Tai*
Affiliation:
Department of Mathematics, University of Bergen, Bergen, Norway
Aaron Fenster*
Affiliation:
Medical Imaging Lab, Robarts Research Institute, University of Western Ontario, London ON, Canada N6A 5B7 Department of Medical Imaging, St Jospeh’s HealthCare, London ON, Canada
*
Corresponding author.Email address:jyuan@robarts.ca
Corresponding author.Email address:bmiles@robarts.ca
Corresponding author.Email address:Greg.Garvin@lhsc.on.ca
Corresponding author.Email address:tai@mi.uib.no
Corresponding author.Email address:afenster@robarts.ca
Get access

Abstract

Image fusion is an imaging technique to visualize information from multiple imaging sources in one single image, which is widely used in remote sensing, medical imaging etc. In this work, we study two variational approaches to image fusion which are closely related to the standard TV-L2 and TV-L1 image approximation methods. We investigate their convex optimization formulations, under the perspective of primal and dual, and propose their associated new image decomposition models. In addition, we consider the TV-L1 based image fusion approach and study the specified problem of fusing two discrete-constrained images 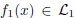and 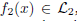where 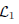and 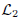are the sets of linearly-ordered discrete values. We prove that the TV-L1 based image fusion actually gives rise to the exact convex relaxation to the corresponding nonconvex image fusion constrained by the discrete-valued set 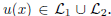This extends the results for the global optimization of the discrete-constrained TV-L1 image approximation [8, 36] to the case of image fusion. As a big numerical advantage of the two proposed dual models, we show both of them directly lead to new fast and reliable algorithms, based on modern convex optimization techniques. Experiments with medical images, remote sensing images and multi-focus images visibly show the qualitative differences between the two studied variational models of image fusion. We also apply the new variational approaches to fusing 3D medical images.

Keywords

68U1090CxxConvex optimizationprimal-dual programmingcombinatorial optimizationtotal-variation regularizationimage fusion
Type
Research Article
Information
Numerical Mathematics: Theory, Methods and Applications , Volume 7 , Issue 2 , May 2014 , pp. 234 - 250
Copyright
Copyright © Global Science Press Limited 2014

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Aiazzi, B., Alparone, L., Baronti, S., and Garzelli, A.. Context-driven fusion of high spatial and spectral resolution images based on oversampled multiresolution analysis. IEEE Geoscience and Remote Sensing, 40(10):2300–2312, 2002.Google Scholar
[2] Aujol, Jean-Fran¸cois, Gilboa, Guy, Chan, Tony F., and Osher, Stanley. Structure-texture image decomposition - modeling, algorithms, and parameter selection. International Journal of Computer Vision, 67(1):111–136, 2006.Google Scholar
[3] Bae, Egil, Tai, Jing Yuan Xue-Cheng, and Boykov, Yuri. A study on continuous max-flow and min-cut approaches part ii: Multiple linearly ordered labels. Technical report CAM-10-62, UCLA, CAM, 2010.Google Scholar
[4] Bertsekas, Dimitri P.. Constrained optimization and Lagrange multiplier methods. Academic Press Inc, New York, 1982.Google Scholar
[5] Boykov, Yuri, Veksler, Olga, and Zabih, Ramin. Fast approximate energy minimization via graph cuts. IEEE PAMI, 23(11):1222–1239, November 2001.Google Scholar
[6] Brainweb. http://www.bic.mni.mcgill.ca/brainweb/. 2011.Google Scholar
[7] Chambolle, A.. An algorithm for total variation minimization and applications. Journal of Mathematical Imaging and Vision, 20(1-2):89–97, Jan 2004.Google Scholar
[8] Chan, Tony F. and Esedoglu, Selim. Aspects of total variation regularized L1 function approximation. SIAM J. Appl. Math., 65(5):1817–1837 (electronic), 2005.Google Scholar
[9] Chan, Tony F., Esedoglu, Selim, and Nikolova, Mila. Algorithms for finding global minimizers of image segmentation and denoising models. SIAM J. Appl. Math., 66(5):1632–1648 (electronic), 2006.Google Scholar
[10] Chan, Tony F. and Vese, Luminita A.. Active contours without edges. IEEE Transactions on Image Processing, 10(2):266–277, 2001.Google Scholar
[11] Collins, D.L., Zijdenbos, A.P., Kollokian, V., Sled, J.G., Kabani, N.J., Holmes, C.J., and Evans, A.C.. Design and construction of a realistic digital brain phantom. IEEE Transactions on Medical Imaging, 17(3):463–468, Jun 1998.Google Scholar
[12] Das, Asha and Revathy, K.. A comparative analysis of image fusion techniques for remote sensed images. In World Congress on Engineering, pages 639–644, 2007.Google Scholar
[13] Ekeland, Ivar and Téeman, Roger. Convex analysis and variational problems. Society for Industrial and Applied Mathematics, Philadelphia, PA, USA, 1999.Google Scholar
[14] Fan, Ky. Minimax theorems. Proc. Nat. Acad. Sci. U. S. A., 39:42–47, 1953.Google Scholar
[15] Giusti, Enrico Minimal surfaces and functions of bounded variation. Australian National University, Canberra, 1977.Google Scholar
[16] Ishikawa, Hiroshi. Exact optimization for markov random fields with convex priors. IEEE PAMI, 25:1333–1336, 2003.Google Scholar
[17] Kluckner, Stefan, Pock, Thomas, and Bischof, Horst. Exploiting redundancy for aerial image fusion using convex optimization. In DAGM, pages 303–312, 2010.Google Scholar
[18] Kk, R.K.-S., Evans, A.C., and Pike, G.B.. Mri simulation-based evaluation of image-processing and classification methods. IEEE Transactions on Medical Imaging, 18(11):1085–1097, Nov 1999.Google Scholar
[19] Li, H., Manjunath, B. S., and Mitra, S. K.. Multisensor image fusion using the wavelet transform. Graphical Models and Image Processing, 57(3):235–245, 1995.Google Scholar
[20] Meyer, Yves. Oscillating patterns in image processing and nonlinear evolution equations, volume 22 of University Lecture Series. American Mathematical Society, Providence, RI, 2001. The fifteenth Dean Jacqueline B. Lewis memorial lectures.Google Scholar
[21] Nez, Jorge, Otazu, Xavier, Fors, Octavi, Prades, Albert, Pal’a, Vicenc, and Arbiol, Roman. Multiresolution-based image fusion with additive wavelet decomposition. IEEE Trans. On Geoscience And Remote Sensing, 37(3):1204–1211, May 1999.Google Scholar
[22] Osher, S., Burger, M., Goldfarb, D., Xu, J., and Yin, W.. An iterative regularization method for total variation-based image restoration. Multiscale Modeling and Simulation, 4(2):460–489, 2006.Google Scholar
[23] Pajares, Gonzalo and Manuel|de la Cruz, Jesôs. A wavelet-based image fusion tutorial. Pattern Recognition, 37(9):1855–1872, 2004.Google Scholar
[24] Piella, Gemma. Image fusion for enhanced visualization: A variational approach. International Journal of Computer Vision, 83(1):1–11, 2009.Google Scholar
[25] Rockafellar, R. T.. Augmented Lagrangians and applications of the proximal point algorithm in convex programming. Math. of Oper. Res., 1:97–116, 1976.Google Scholar
[26] Rudin, L., Osher, S., and Fatemi, E.. Nonlinear total variation based noise removal algorithms. Physica D, 60(1-4):259–268, 1992.Google Scholar
[27] Schowengerdt, Robert A.. Remote Sensing: Models and Methods for Image Processing. Elsevier, 3rd edition, 2007.Google Scholar
[28] Sohn, Moon-Jun, Lee, Dong-Joon, Yoon, Sang Won, Lee, Hye Ran, and Hwang, Yoon Joon. The effective application of segmental image fusion in spinal radiosurgery for improved targeting of spinal tumours. Acta Neurochir, 151:231–238, 2009.Google Scholar
[29] Wang, Wei-Wei, Shui, Peng-Lang, and Feng, Xiang-Chu. Variational models for fusion and denoising of multifocus images. IEEE Signal Processing Letters, 15:65–68, 2008.Google Scholar
[30] Wang, Zhijun, Ziou, D., Armenakis, C., Li, D., and Li, Qingquan. A comparative analysis of image fusion methods. IEEE Geo. and Res., 43(6):1391–1402, June 2005.Google Scholar
[31] Wu, Chunlin and Tai, Xue-Cheng. Augmented lagrangian method, dual methods, and split bregman iteration for rof, vectorial tv, and high order models. SIAM J. Imaging Sciences, 3(3):300–339, 2010.Google Scholar
[32] Yang, L., Guo, B.L., and W.Ni., Multimodality medical image fusion based on multiscale geometric analysis of contourlet transform. Neurocomputing, 72:203–211, 2008.Google Scholar
[33] Yin, Wotao, Goldfarb, Donald, and Osher, Stanley. The total variation regularized l1 model for multiscale decomposition. Multiscale Modeling and Simulation, 6(1):190–211, 2007.Google Scholar
[34] Yuan, J., Bae, E., Tai, X.C., and Boykov, Y.. A continuous max-flow approach to Potts model. In ECCV 2010, 2010.Google Scholar
[35] Yuan, Jing, Bae, Egil, and Tai, Xue-Cheng. A study on continuous max-flow and min-cut approaches. In CVPR 2010, pages 2217–2224, 2010.Google Scholar
[36] Yuan, Jing, Shi, Juan, and Tai., Xue-Cheng A convex and exact approach to discrete constrained tv-l1 image approximation. Technical Report CAM-10-51, UCLA, CAM, 2010.Google Scholar