No CrossRef data available.
Article contents
Product Gaussian Quadrature on Circular Lunes
Published online by Cambridge University Press: 28 May 2015
Abstract
Resorting to recent results on subperiodic trigonometric quadrature, we provide three product Gaussian quadrature formulas exact on algebraic polynomials of degree n on circular lunes. The first works on any lune, and has 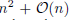 cardinality. The other two have restrictions on the lune angular intervals, but their cardinality is
cardinality. The other two have restrictions on the lune angular intervals, but their cardinality is 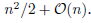
Information
- Type
- Research Article
- Information
- Numerical Mathematics: Theory, Methods and Applications , Volume 7 , Issue 2 , May 2014 , pp. 251 - 264
- Copyright
- Copyright © Global Science Press Limited 2014
References
[1]
Bauman, B. and Xiao, H., Gaussian quadrature for optical design with noncircular pupils and fields, and broad wavelength range, Proc. SPIE
7652(2) (2010), 1–12.Google Scholar
[2]
Bos, L. and Vianello, M., Subperiodic trigonometric interpolation and quadrature, Appl. Math. Comput.
218 (2012), 10630–10638.Google Scholar
[3]
Da Fies, G., Sommariva, A. and Vianello, M., Algebraic cubature by linear blending of elliptical arcs, Appl. Numer. Math.
74 (2013), 49–61.CrossRefGoogle Scholar
[4]
Da Fies, G. and Vianello, M., Algebraic cubature on planar lenses and bubbles, Dolomites Res. Notes Approx.
5 (2012), 7–12.Google Scholar
[5]
Da Fies, G. and Vianello, M., Trigonometric Gaussian quadrature on subintervals of the period, Electron. Trans. Numer. Anal.
39 (2012), 102–112.Google Scholar
[6]
Da Fies, G. and Vianello, M., On the Lebesgue constant of subperiodic trigonometric interpolation, J. Approx>. Theory
167 (2013), 59–64.Google Scholar
[7]
Da Fies, G., Sommariva, A. and Vianello, M., Matlab functions for subperiodic trigonometric quadrature and for product Gaussian quadrature on circular sections, online at: http://www.math.unipd.it/∼marcov/CAAsoft.html.Google Scholar
[8]
Gautschi, W., Orthogonal Polynomials: Computation and Approximation, Oxford University Press, New York, 2004.Google Scholar
[9]
Gautschi, W., Orthogonal polynomials (in Matlab), J. Comput. Appl. Math.
178 (2005), 215–234, software online at: http://www.cs.purdue.edu/archives/2002/wxg/codes.Google Scholar
[10]
Gautschi, W., Sub-range Jacobi polynomials, Numer. Algorithms
61 (2012), 649–657.Google Scholar
[11]
Langton, S.G., The quadrature of lunes, from Hippocrates to Euler, Euler at 300, 5362, MAA Spectrum, Math. Assoc. America, Washington, DC, 2007.Google Scholar
[12]
Meurant, G. and Sommariva, A., Fast variants of the Golub and Welsch algorithm for symmetric weight functions in Matlab, Numer. Algorithms, published online 23 November 2013.Google Scholar
[13]
Pleśniak, W., Multivariate polynomial inequalities via pluripotential theory and subanalytic geometry methods, Banach Center Publ.
72 (2006), 251–261.CrossRefGoogle Scholar
[14]
Pleśniak, W., Multivariate Jackson Inequality, J. Comput. Appl. Math.
233 (2009), 815–820.Google Scholar
[15]
Postnikov, M.M., The problem of squarable lunes, American Mathematical Monthly
107 (2000), 645–651 (translated from the Russian by Abe Shenitzer).Google Scholar
[16]
Santin, G., Sommariva, A. and Vianello, M., An algebraic cubature formula on curvilinear polygons, Appl. Math. Comput.
217 (2011), 10003–10015.Google Scholar
[17]
Sommariva, A. and Vianello, M., Gauss-Green cubature and moment computation over arbitrary geometries, J. Comput. Appl. Math.
231 (2009), 886–896.Google Scholar
[18]
Stasica, J., The Whitney condition for subanalytic sets, Zeszyty Nauk. Uniw. Jagiellon. Prace Mat.
23 (1982), 211–221.Google Scholar

