Introduction
Demographic models are useful tools to understand population trends and the influence of demographic parameters (Lebreton & Clobert, Reference Lebreton, Clobert, Perrins, Lebreton and Hirons1991) and to evaluate strategies for conservation (Sarrazin & Legendre, Reference Sarrazin and Legendre2000). Such models can also be used to anticipate future population trends (Wootton & Bell, Reference Wootton and Bell1992). Demographic studies in birds of prey have been carried out mainly in declining populations (Whitfield et al., Reference Whitfield, Fielding, Mcleod and Haworth2004), and less attention has been paid to the demographic processes underlying recovering populations (Wyllie & Newton, Reference Wyllie and Newton1991; Ferrer & Donázar, Reference Ferrer and Donázar1996). However, the indicators of demographic health or sensitivity to demographic parameters in growing populations can differ from those observed in declining populations and, therefore, the diagnostic tools and the conservation strategies may be different (Katzner et al., Reference Katzner, Milner-Gulland and Bragin2007).
The Spanish imperial eagle Aquila adalberti is categorized as Vulnerable on the IUCN Red List (Birdlife International, 2004; IUCN, 2007) and recovered from 38 pairs in the 1970s to c. 200 pairs in 2004 (González & Oria, Reference González, Oria, Madroño, González and Atienza2004). This offers the possibility of analysing the demographic processes associated with a population recovery. The demography of the population of 8–15 pairs in Doñana has already been analysed (Ferrer & Calderón, Reference Ferrer and Calderón1990; Ferrer & Donázar, Reference Ferrer and Donázar1996; Ferrer & Bisson, Reference Ferrer and Bisson2003; Ferrer et al., Reference Ferrer, Penteriani, Balbontín and Pandolfi2003) but there is no published information on the demography of the largest part of the population. In this context the aims of this research were to (1) describe and analyse the geographical variation of the species' population trend during 1981–2004, (2) estimate the main demographic parameters and analyse their spatial and temporal variation, (3) build a demographic model to relate these variations to the species' population trend, and (4) make recommendations for the conservation of the species.
Methods
All known breeding territories of the species up to 2004 (González & Oria, Reference González, Oria, Madroño, González and Atienza2004; González et al., Reference González, Oria, Margalida, Sánchez, Prada and Caldera2006b) were grouped into five geographical areas: North, Centre, West, South and Doñana (Fig. 1), based on the species' breeding area in 2004 (González et al., Reference González, Oria, Sánchez, Margalida, Aranda and Prada2008). Breeding territories were clumped in the same area if they were < 20 km apart and belonged to a similar geographical and habitat unit. The data come from 10 national censuses of the species, in 1974 (Garzón, Reference Garzón1974), 1981–1986 (González et al., Reference González, González, Garzón and Heredia1987), 1989 (González, Reference González1991), 1994 (González, Reference González, Muntaner and Mayol1996), and 1999, 2000, 2001, 2002, 2003 and 2004 (González & Oria, Reference González, Oria, Madroño, González and Atienza2004); each census covered the species' whole range. We focus on North, Centre, West and South, which account for 95% of the population (Fig. 2). A total of 220 territories, which were occupied with variable frequency, were monitored in these censuses. Except for the 1974 census, LMG, JO and RS participated in and coordinated the censuses. Previous work has shown the existence of three periods of population growth during the recovery period: 1981–1993, 1994–1999 and 2000–2004 (González, Reference González, Muntaner and Mayol1996; González & Oria, Reference González, Oria, Madroño, González and Atienza2004). Comparisons of observed with expected trends were conducted with a Student t-test for related samples, comparing results of the real counts with the number of pairs predicted by the model.

Fig. 1 The five areas of the distribution of the Spanish imperial eagle (see text for further details); 95% of the population occurs in North, South, West and East, and only these areas were considered in this study.

Fig. 2 Changes in the number of pairs of the Spanish imperial eagle in the five areas (Fig. 1) from the results of 10 national censuses.
A Leslie matrix model structured in four age classes was constructed (Fig. 3). We modelled only the female fraction of the population. The model took the average date of birth to be 15 April and the beginning of the post-fledging period to be 1 July (Margalida et al., Reference Margalida, González, Sánchez, Oria, Prada and Caldera2007). The dependence period of fledglings was assumed to last until 1 October (Alonso et al., Reference Alonso, González, Heredia and González1987). At the beginning of each reproductive cycle, 1 January, four possible age classes were considered: age 1, individuals 0.7 years old; age 2, individuals 1.7 years old; age 3, individuals 2.7 years old; age 4, individuals ≥ 3.7 years old. The model included the following parameters:

Fig. 3 Leslie matrix of the model for the population of the Spanish imperial eagle i, where n 1, n 2, n 3 and n 4 are the numbers of females of each age group, t is time in years, So survival during post-fledging, Sd survival of the dispersers, S3 survival of the third to fourth age group, Sa survival of the breeders, б is the proportion of fledgling females, P3 and P4 are the productivity of the females in the third and fourth age classes, respectively, and γ3 and γ4 are the proportion of breeding females in each of these groups.
So, survival from fledging until independence (the same value was assumed for all models);
Sd, annual survival during the dispersal period, 0.7–2.7 years of age, using the same value in all simulations;
Sa, annual survival of breeders ≥ 3.7 years old;
S3, annual survival rate over 2.7–3.7 years, could not be directly estimated because of the lack of radio tracking data for this period, and was therefore calculated in all cases as the average of Sa and Sd, weighted according to the proportion of age 3 birds that are assumed to breed (γ 3; Fig. 3; in this way we assumed that survival before settlement on a breeding territory was low and only rose after settlement);
P3, average number of chicks fledged by age 3 females;
P4, average number of chicks fledged by age 4 females;
σ, proportion of females among fledglings, set as 0.5 in all cases.
We used the software ULM 4.0 (Legendre, Reference Legendre2003) to run the model. One hundred random trajectories were drawn by randomly changing the productivity and survival parameters each year, considering the productivity values P3 and P4 as stochastic variables with mean and variance following a log-normal distribution, and survival rates So, Sd, and Sa as stochastic variables with mean and variance following a beta distribution. We used the total variance, which integrates the inter-annual and inter-territorial variability of productivity. In this way, we estimated the average population growth rate λe and its associated standard errors under different scenarios. Firstly, we built a global model considering all the geographical aggregations as a single population going through three phases of population growth, 1981–1993, 1994–1999 and 2000–2004, each with its own estimated demographic parameters. The initial number of individuals in each age group (n i) at the start of the simulation in 1981 was estimated by interpolation from the results of the 1974 and 1986 censuses, assuming that the population was in equilibrium. The initial number of individuals in each age class for each successive period corresponds to the output values of the previous period, leaving the simulations for the three periods linked. Secondly, we estimated the growth rate of each geographical area independently, to evaluate the average demographic balance in each during 1981–2004. The estimated growth rates were compared with observed growth rates λo, which were calculated as λo = (Nt/N 0)1/t (Lande, Reference Lande1988), where Nt is the final observed population size, N 0 is the initial observed population size and t is the number of years between the two counts.
Sensitivity and elasticity analysis implemented in ULM were conducted to see the effect of changes in each parameter on the estimated population growth rates. Considering the demographic parameters estimated for 2000–2004, we evaluated the current demographic viability of the population as the probability of extinction for each geographical aggregation in the next 50 and 100 years in the worst scenario, i.e. considering each population as isolated. This was performed using Monte Carlo simulations as implemented in ULM. The probability of extinction at the end of the simulation period was calculated as the proportion of 100 trajectories in which the modelled population went extinct.
We estimated observed productivity (number of fledglings per occupied territory) from nest survey data obtained from 1981 and 2004, involving 1,781 breeding attempts (292, 484, 744 and 261 in Centre, West, North and South, respectively). A detailed account of the monitoring methods is given in Margalida et al. (Reference Margalida, González, Sánchez, Oria, Prada and Caldera2007). We computed independent estimates of productivity for females of age 3 (P 3) and for females of age 4 (P 4). The average and inter-annual standard deviation of each productivity parameter were calculated for each of the above mentioned periods and geographical aggregations. The average productivity of the populations was calculated for each year, and these values subsequently averaged for all the years included in a given period. Temporal and spatial differences in productivity values were tested with an analysis of variance and Tukey tests (Zar, Reference Zar1984).
We estimated actual survival rates based on the monitoring of radio-tagged individuals or of those easily identifiable by natural markings (patterns of the white feathers on the leading edge of the wing). Standard errors for survival rates were calculated assuming a binomial distribution of these variables, according to ((S(1 – S))/n)2, where S is the survival rate and n is the sample size.
Over 1990–2001 we radio tagged 66 chicks at the nest (33 males, 27 females and six of indeterminate sex) and radio tracked them until independence. Survival during the post-fledging period, So, was calculated as the percentage of these young that were still alive on 1 October, after a period of parental dependency of c. 3 months (Alonso et al., Reference Alonso, González, Heredia and González1987).
We estimated actual survival rates of dispersers (Sd) and of breeders (Sa; ± 95% confidence interval) by analysing sighting-resighting histories of individuals from year to year, with the software MARK (Burnham & Anderson, Reference Burnham and Anderson1998; White & Burnham, Reference White and Burnham1999). The sample analysed by MARK is not the set of year to year events for an individual but the set of histories, which are independent of one another. MARK estimates the actual survival rates as the parameters of a model obtained by means of adjusting these sighting-resighting data to several models and selecting the one that best explains the observed data. In accordance with the nature of the available information, a combination of resighting (birds found alive) and of recoveries (birds found dead), we used the model Both Burnham (White & Burnham, Reference White and Burnham1999) that considers four parameters: S, the probability of surviving from one interval to the next (survival rate); p, the probability of resighting a marked individual alive; F, the probability that a marked individual remains in the area between two periods (philopatry); and r, the probability of a dead marked individual being recovered. In South, where the records only included resightings of individuals but no recoveries, a recaptures-only model was used, which only considers two parameters, S and p. Goodness of fit tests were conducted with 1,000 iterations, adjusting the models when necessary. Among the models produced to fit our observed data, we selected the most parsimonious on the basis of the minimum Akaike Information Criterion (AIC). The significance of the parameters on the models was evaluated using Likelihood Ratio Test.
We estimated actual annual survival during dispersal, Sd, from the radio tracking of 52 individuals (26 males, 23 females and three of unknown sex), tagged in 1990–2001, after leaving the parental territory. In each of the five 6-month intervals following the onset of dispersion (1 October), each individual was considered as found alive, found dead, not found or not tracked. This data set was used to estimate the 6-month survival rate, which was squared to obtain the annual survival rate.
From 1989–2004 the annual monitoring of breeding territories provided information on the actual survival of 157 territorial individuals ≥ 3.7 years old, Sa (143 based on natural markings and 14 based on radio tracking). At the start of each breeding season each individual was considered as alive, not found, or found dead. Estimates of survival rates of breeders were computed for 1989–1993, 1994–1999 and 2000–2004 (22, 76 and 76 individuals, respectively). The individuals whose records cover more than one period were considered in each of the respective simulations. Average survival rates of breeders was estimated for 1989–2004 in Centre (n = 14 individuals), North (n = 44) and West (n = 31) and for 1994–2004 in South (n = 18), according to the availability of monitoring data. We also tested for differences in survival between sexes, considering data from 66 females and 65 males from Centre, North and West, for which this information was available.
The proportion of females breeding at 3 years of age (γ3) was estimated from radio-tagged birds that were tracked at least until their third year of life during 1994–1999.
For each year territorial birds were categorized as adults or non-adults, as described in Margalida et al. (Reference Margalida, González, Sánchez, Oria, Prada and Caldera2007). Based on this, we calculated the annual proportion of territorial birds that were non-adults.
Results
The breeding population of the Spanish imperial eagle in the areas considered includes 95% of the breeding pairs of the species in 2004, the number of which has increased from 25 to 188 breeding pairs between 1974 and 2004 (Garzón, Reference Garzón1972, Reference Garzón1974; González et al., Reference González, González, Garzón and Heredia1987; González, Reference González1991, Reference González, Muntaner and Mayol1996; González & Oria, Reference González, Oria, Madroño, González and Atienza2004), rising at an average of 5.4 pairs per year. However, three different phases or periods in the evolution of the population can be identified (Fig. 4). Over 1974–1993 numbers rose from 25 to 127 pairs (average growth of 5.1 pairs per year), over 1994–1999 the population was 127–131 pairs, and over 2000–2004 the number of pairs rose from 131 to 188 (average increase of 14.2 pairs per year). The species increased in numbers in all areas except Doñana (Fig. 2).

Fig. 4 Observed evolution of the number of breeding pairs of Spanish imperial eagles in Centre, West, North and South combined (continuous line) and the predicted evolution of the population according to the results of the simulation model (broken line; see text for further details), with 95% confidence interval.
We did not find statistically significant differences in average productivity P between the three periods (Table 1), although it increased slightly in the last two compared to the first (F 2,21 = 0.79, P = 0.47). Average annual productivity was higher in Centre and South and lower in West (F 3,91 = 7.78, P = 0.0001). Multiple comparison analyses showed that the average annual productivity in West differs significantly from that of Centre (Tukey test, P = 0.001) and South (Tukey test, P = 0.001).
Table 1 Demographic parameters considered for each period and area (Fig. 1). Sd is the estimated annual survival during the dispersal period; Sa the estimated annual survival of breeders; n i the estimated number of females within each age class at the start of each period (as in the Leslie matrix, Fig. 3; see text for further explanation); P 3 the observed average number of chicks fledged by 3-year old females; P 4 the observed average number of the chicks fledged by 4-year old females; λ average population growth rate. The following parameters were kept constant in all periods and areas: proportion of females of age 4 that start breeding, γ4 = 1; proportion of females of age 3 that start breeding, γ3 = 0.125; survival rate during the fledging period, S0 = 0.894 ± 0.037).

The observed survival during the post-fledging period of 3 months, So, was 0.894 (n = 66), 0.818 in males (n = 33) and 0.963 in females (n = 27), although this difference was not significant (Fisher's exact test, P = 0.12). The equivalent annual survival rate would be 0.638 (0.447 for males and 0.860 for females).
To estimate the observed survival rate during dispersal (Sd) the selected model considered all parameters to be constant except r, which was considered to be dependent on time (LRT test χ24 = 30.57, P < 0.0001). The observed 6-month survival rate during the dispersal period was thus 0.749 ± SE 0.037, which produces an average annual survival rate of 0.561 ± SE 0.067. Combining So and Sd, we can estimate an overall observed survival rate of 0.579 for the first year of life after fledging, and a global observed survival rate from fledging to the start of the fourth calendar year of 0.243 and of 0.136 to the start of the fifth calendar year.
The most parsimonious model to estimate the observed annual survival of breeders, Sa, in each of the three periods considered all model parameters as constant throughout each period. The values of adult survival were 0.986 ± SE 0.061 for 1989–1993, 0.918 ± SE 0.032 for 1994–1999 and 0.933 ± SE 0.052 for 2000–2004. When considering the different areas, a better fit was obtained with a model that considers all parameters as constant except survival (Sa), which was considered to be dependent on the area (LRT, χ22 = 13.38, P = 0.0012). The resulting estimates of observed survival rates of breeders in each area were Sa = 0.967 ± SE 0.023 for Centre, Sa = 0.953 ± SE 0.013 for West, Sa = 0.819 ± SE 0.016 for North and Sa = 0.914 ± SE 0.034 for South. The overall observed survival rates of breeders was found to be independent of sex, and the global observed survival rate of breeders for all areas, periods and sexes combined was estimated as Sa = 0.915 ± SE 0.012.
Two of the 80 radio-tagged females that reached age 3 over 1994–1999 were established as breeders at this age, giving an estimate of the observed proportion of breeding females at 3 years of age, γ3, of 0.125.
The annual proportion of breeders in non-adult plumage was 0–14.3% (Fig. 5). Over 1981–1990 values were always < 7%. From 1991–2004 onwards, the annual percentage of territorial birds with non-adult plumage was 7–14.3%. During this period the lowest values (7–10%) coincided with the period of stabilization of the population (1994–1999), while the periods of increase (1981–1993, 2000–2004) were characterized by values > 10%.

Fig. 5 Observed trend of the of the number of breeding pairs of Spanish imperial eagle in Centre, West, North and South combined (continuous line) and the percentage of non-adult birds (black dots) in the breeding population.
The model predicted population growth for the three periods, as the confidence interval for λ always excludes 1 (Table 1). Observed rates of increase were clearly below the 95% confidence interval of expected rates of increase during the second period and above during the third period (Table 1). However, the population counts predicted by our model showed a good fit to the observed evolution of the population in the first (Student t-test for related samples, t 1 = 0.67, P = 0.63) and second (t 2 = 1.09, P = 0.39) periods, but not in the third period (t 3 = 3.99, P = 0.028; Fig. 4). Unrealistic increases of Sa during this latter period are needed to improve the fit (Fig. 6). However, different simulations using combinations of γ3 ranging from 0.125 (the value estimated in this study for 1994–1999) to 0.50 (the value observed for 2000–2006, authors’ own data, n = 8) and of Sd, ranging from 0.561 (the value estimated in this study) to 0.743 (the highest value reported for the species; Ferrer et al., Reference Ferrer, Otalora and García-Ruiz2004) were able to improve the fit to the observed trend in 2000–2004 (Fig. 6). Although the eagle population had positive observed growth rates in all the areas considered, expected growth rates were only positive in Centre, West and South and negative in North. Observed λ values were particularly divergent from 95% confidence intervals of expected λ in North and South, in which the eagle population performed much better than predicted.

Fig. 6 Difference between the observed trends in the Spanish imperial eagle population and simulated trajectories from the model (see text for details) using different combinations of parameters. The simulation trajectories until 1999 are as in Fig. 4. For 2000–2004 we illustrate several simulations with variable values of Sa, keeping the other parameters as in Fig. 4 (a), and several combinations of Sd and γ3, keeping the other parameters as in Fig. 4 (b). Note the different y-axis scales.
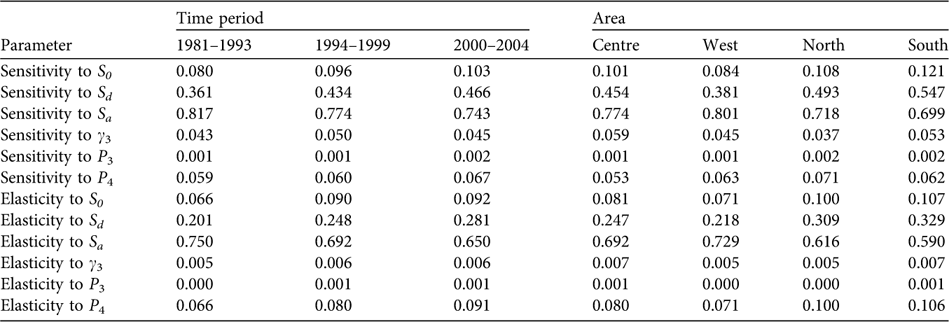
The population proved to be especially sensitive to variations in the survival rate of breeders (sensitivity values of 0.743–0.817 and elasticity of 0.650–0.750) and, to a lesser extent, to the survival rates of individuals during dispersion (sensitivity values of 0.361–0.466 and elasticity of 0.201–0.281) and to post-fledging survival (Table 2). Over the years, a decrease is seen in sensitivity to the adult survival rate and a relative increase in sensitivity to the rest of the population parameters, especially to survival during the dispersal phase. Considering the demographic parameters for 2000–2004, the probability of extinction in the next 50 and 100 years for the whole population studied was 0, and also in West, Centre and South considered independently. In North the probabilities of extinction in the next 50 and 100 years were 0.25 and 1, respectively.
Discussion
The population of the Spanish imperial eagle has experienced a spectacular recovery over 1974–2004. The rate of recovery went through a period of increase (1981–1993), a period of stability (1994–1999) and a period of further increase (2000–2004; González & Oria, Reference González, Oria, Madroño, González and Atienza2004). The analysis of the temporal and spatial variation of breeding success and adult survival helps to explain the demographic mechanisms underlying this pattern. Productivity has remained more or less constant and thus variations in breeding success do not appear to explain the temporal variations of the observed population growth rates. The temporal and spatial variation in recovery rates matches the changes in adult survival in the different periods. The implementation of conservation actions for the species probably contributed to the maintenance of a high survival rate during 1981–1993. However, adult survival was significantly reduced during 1994–1999 as a consequence of an increase in the use of illegal poison in South and North (González et al., Reference González, Margalida, Mañosa, Sánchez, Oria and Molina2007), which were more affected by the decline in growth rates. The last period of population growth again coincided with an increase in adult survival, probably associated with a decline in the number of poisoning events (González et al., Reference González, Margalida, Mañosa, Sánchez, Oria and Molina2007). Thus, in agreement with previous demographic studies (Ferrer & Calderón, Reference Ferrer and Calderón1990; Real & Mañosa, Reference Real and Mañosa1997; Katzner et al., Reference Katzner, Bragin and Milner-Gulland2006), high adult survival is the main parameter explaining increase of the population and the observed temporal and spatial variation in population growth rates.
However, changes in adult survival may not have been acting alone. Although there are no previous published estimates of survival rate during the dependence period (from fledging to initiation of dispersal) for the Spanish imperial eagle, we found a relatively high value in comparison to similar species (Real & Mañosa, Reference Real and Mañosa1997), possibly as a consequence of the implementation of supplementary feeding programmes (González et al., Reference González, Margalida, Sánchez and Oria2006a). On the other hand, our results indicate a relatively low annual survival rate during dispersal in comparison to previous estimates (Penteriani et al., Reference Penteriani, Otalora and Ferrer2006). Our estimate corresponds to 1990–2001, when a steady decline in rabbit availability due to hemorragic disease was recorded (Villafuerte et al., Reference Villafuerte, Calvete, Blanco and Lucientes1995), which may have had a severe impact on the survival of dispersing eagles (Penteriani et al., Reference Penteriani, Otalora, Sergio and Ferrer2005). Globally, however, our estimate of survival from fledging to the start of the fourth or fifth calendar year is similar to previous estimates for the species (Ferrer & Calderón, Reference Ferrer and Calderón1990).
Our model reproduced fairly well the behaviour of the population during 1981–1999, but during 2000–2004 the observed increase in the number of pairs was more than expected from the model. This discrepancy may be partially caused by an increase in monitoring effort during this period. Another potential source of bias could be the use of incorrect parameter estimates for this period. This is unlikely, however, because adult survival and productivity values were both estimated from large sample sizes. Moreover, simulated increases of productivity or adult survival during this period were not sufficient to reproduce the observed population increase. A more likely explanation is an underestimation of pre-adult survival or of the proportion of 3-year old females starting to breed, as the values used in the model were based on data collected in earlier periods. Manipulation of one or both of these parameters within biologically reasonable values for this period improved the fit to the real trajectory of the population, indicating that variation of one or both of these parameters may be the cause of the increase and expansion of the species from 2000 onwards.
The total population growth rate is not particularly sensitive to variations in Y3 because productivity of age 3 females is low but this parameter does have a large direct influence on the number of breeding pairs. A decrease in the age of first breeding in recent years may be the cause of the noticeable rapid increase of the breeding population during 2000–2004. This is consistent with the increase in the proportion of breeders with non-adult plumage in 2000–2004, particularly in recently established territories but not in older ones (Margalida et al., Reference Margalida, González, Sánchez, Oria, Prada and Caldera2007), and also with the increase in the proportion of third year females that started breeding in 2000–2004 (Margalida et al., Reference Margalida, Mañosa, González, Ortega, Oria and Sánchez2008). Although a high proportion of non-adults in breeding pairs may be taken as an indicator of a declining population in stable populations with high adult mortality (Balbontín et al., Reference Balbontín, Penteriani and Ferrer2003; Ferrer et al., Reference Ferrer, Penteriani, Balbontín and Pandolfi2003), this may not be so in all situations (Katzner et al., Reference Katzner, Milner-Gulland and Bragin2007; Margalida et al., Reference Margalida, Mañosa, González, Ortega, Oria and Sánchez2008). In fact, during the initial period of population increase we observed low and high values of the proportion of non-adults in breeding pairs. From 1990 onwards the proportion of non-adults in breeding pairs appeared to fluctuate inversely with growth rate. This indicates that the magnitude of this parameter may be dependent on several factors and that its meaning and interpretation is not straight forward (Katzner et al., Reference Katzner, Milner-Gulland and Bragin2007). In an increasing population, such as that studied here, this high proportion of non-adult birds in the breeding population may be the result of colonization, i.e. the occupation of new territories by immature or subadult birds (González et al., Reference González, Oria, Margalida, Sánchez, Prada and Caldera2006b; Margalida et al., Reference Margalida, González, Sánchez, Oria, Prada and Caldera2007). However, the factors underlying this general decrease in the age of first breeding in the Spanish imperial eagle in 2000–2004 are still not understood, although it could be related to an increase in food or nest site availability (Margalida et al., Reference Margalida, González, Sánchez, Oria, Prada and Caldera2008). We know that the main factor that explains the population recovery of this eagle in the last century was their ecological plasticity in the selection of breeding habitats as a response to human pressures (González et al., Reference González, Oria, Sánchez, Margalida, Aranda and Prada2008). On the other hand, a general improvement in food availability in dispersal areas associated with the recovery of rabbit populations after 2000 may have triggered a possible increase in pre-adult survival relative to values in the previous decade.
During the study period the species has increased in numbers across its distribution range, except in Doñana, where it has been suggested that the population is saturated (Ferrer et al., Reference Ferrer, Penteriani, Balbontín and Pandolfi2003, although see Beja & Palma, Reference Beja and Palma2008). The population viability analysis failed to detect any global population imbalance and indicated that as long as adult and pre-adult survival are high the population is not at risk in the short-term. However, future habitat or anthropogenic changes in the breeding or in the dispersal areas could have unexpected effects on the population parameters. As expected from other studies (Real & Mañosa, Reference Real and Mañosa1997; Katzner et al., Reference Katzner, Milner-Gulland and Bragin2007), we found that the population growth rate is highly sensitive to variation in the survival rates of breeders and, to a lesser extent, to the survival of dispersing individuals. We found that the sensitivity of λ to pre-adult survival rates was higher in those areas that showed the largest discrepancy between observed and expected growth rate, and also that sensitivity to this parameter increased during the study period. This indicates that when and where the relative importance of non-adult birds in the population increases, population growth rate becomes more sensitive to the population parameters affecting this fraction of the population.
The observed population trends were close to those predicted by the simulation models in Centre and West, whereas in North and South the observed trends were substantially higher than predicted. A possible explanation for these discrepancies could be an unaccounted exchange of individuals between areas. We hypothesize that West would have acted as a donor population for other areas. North, where predicted tendency was to decrease, would have been a sink for individuals (Whitfield, Reference Whitfield, Fielding, McLeod and Haworth2003) from other areas. Because of its proximity, West is the likely origin of the North population individuals. This would also explain why the West population has fluctuated in tandem with that of North in recent decades. Current population trends (stabilization) and breeding parameters (low productivity) in these two areas indicate that they are probably saturated, whereas Centre and South are still able to increase. This pattern of population flow is supported by natal dispersal information (González et al., Reference González, Oria, Margalida, Sánchez, Prada and Caldera2006b), and explains the light genetic structuring found between these areas (Martínez-Cruz et al., Reference Martínez-Cruz, Godoy and Negro2004).
Our results indicate that the population of the Spanish imperial eagle has a positive demographic trend. Nonetheless, habitat changes or human activities could alter this situation, causing changes in productivity or survival that could alter the demography of the species. Adult mortality is the main factor driving population trends but the population is becoming more sensitive to pre-adult survival rates, confirming previous studies showing it may be a key factor for the conservation of breeding populations (Penteriani et al., Reference Penteriani, Otalora, Sergio and Ferrer2005, 2006). These results highlight the need to increase efforts to preserve high adult survival, to identify dispersal areas, and to monitor and promote the survival of non-mated eagles. A generalized decline in the age of first reproduction is taking place, which allowed the rapid expansion of the species but may have implications for future performance and management of the species in its breeding areas. Also, local declines in productivity and adult survival in some breeding areas could have negative effects on other breeding areas with high survival. As all areas occupied by the species seem to be demographically connected, coordinated management of the species across its range is required.
Acknowledgements
We are indebted to F. Aparicio, L. Bolonio, J.A. Blanco, J.P. Castaño, M.A. Cedenilla, L. Corraleche, C. Dávila, F. de Antonio, A. Espinosa, A. Gil, J. Guzmán, R. Jiménez, L. López, J. López, I. López, D. Martín, C. Molina, E. Morales, S. Pacheco, F. Robles, J. Sánchez-Mateos, J. Sanz, A. Sierra, C. Soria, R. Tomás, M. Panadero and J. Panadero. We also thank R. Moreno-Opo, F. Silvestre, L. García, C. Urdiales, A. Arredondo, J.L. González, F. Güil, S. Agudín, N. El Khadir, P. Garzón, J. Garzón, D. Martín, M. Fernández, P. Maldonado, T. Gullick and J.L. Freije for their participation in collecting the field data, and especially to J. Caballero, V.G. Matarranz, S. Centenera, B. Heredia, F. Montoto, J. Jiménez, A. Gómez and C. Rodríguez-Vigal. We also thank the staff of the Wildlife Services of the Autonomous Communities of Madrid, Castilla y León, Castilla-La Mancha and Extremadura, especially A. Aranda, J.M. Blanco, I. Mosqueda, A. Rodríguez, A. Sánchez, M.J. Palacios, J. Caldera, L. Prada, J.I. Molina, F. Sánchez, N. González and F. Jiménez. We are also grateful to the landowners that participate in the LIFE projects. The comments of T. Katzner and an anonymous reviewer improved the manuscript. M. López and M. Cubedo (University of Barcelona) collaborated in the statistics. The field work was funded by the Consejerías de Medio Ambiente of Madrid, Castilla y León, Castilla-La Mancha and Extremadura. This study was funded by the Dirección General para la Biodiversidad through TRAGSA and Fundació Bosch i Gimpera of the University of Barcelona, and the European Commission through LIFE project 03/NAT/E/000050.
Biographical sketches
Enric Ortega is interested in the conservation of birds of prey. Santi Mañosa has devoted most of his research to the ecology and conservation of birds of prey. Antoni Margalida mainly carries out research on the behavioural ecology and conservation of vultures. Roberto Sánchez and Javier Oria are interested in the conservation of endangered birds of prey. Luis Mariano González's research interests lie in the recovery of threatened species.