Detecting tropical wildlife declines through camera-trap monitoring: an evaluation of the Tropical Ecology Assessment and Monitoring protocol

Abstract

Identifying optimal sampling designs for detecting population-level declines is critical for optimizing expenditures by research and monitoring programmes. The Tropical Ecology Assessment and Monitoring (TEAM) network is the most extensive tropical camera-trap monitoring programme, but the effectiveness of its sampling protocol has not been rigorously assessed. Here, we assess the power and sensitivity of the programme's camera-trap monitoring protocol for detecting occupancy changes in unmarked populations using the freely available application PowerSensor!. We found that the protocol is well suited to detect moderate (≥ 5%) population changes within 3–4 years for relatively common species that have medium to high detection probabilities (i.e. p > 0.2). The TEAM protocol cannot, however, detect typical changes in rare and evasive species, a category into which many tropical species and many species of conservation concern fall. Additional research is needed to build occupancy models for detecting change in rare and elusive species when individuals are unmarked.

Camera-trap surveys have become a popular technique for assessing change in wildlife populations (O'Brien, 2016). The Tropical Ecology Assessment and Monitoring (TEAM) network is the most extensive tropical camera-trap programme, monitoring terrestrial wildlife in 17 tropical forests. The programme's mission is to provide an early warning system for the status of biodiversity by monitoring > 500 populations of ground-dwelling mammals and birds (Beaudrot et al., 2016). The camera-trap data have been used to evaluate wildlife trends within and across protected areas and to assess the effectiveness of protected areas in maintaining wildlife populations (Ahumada et al., 2011, 2013; Beaudrot et al., 2016). However, the power of TEAM's protocol to detect occupancy changes has not been assessed. Like many camera-trap monitoring programmes, TEAM has hitherto relied on rules of thumb and common practices for survey design, in particular for determining the number of points to survey and the duration of sampling at each point. Specifically, TEAM has deployed camera traps across a grid of 60–90 points at a density of 1–2 per km² in each forest. Field assistants activate the cameras annually for 1 month (30 sampling days).

Here, we assess the power and sensitivity of the programme's sampling design and its camera-trap monitoring protocol (TEAM Network, 2011; Jansen et al., 2014). We use PowerSensor! (TEAM Network, 2018) to calculate the sensitivity of wildlife occupancy trends based on the number of sampling points and the sampling duration for populations with varying levels of initial occupancy and detectability. Specifically, we assess the sensitivity of the TEAM protocol to annual linear occupancy declines ranging from severe (15%) to small (1%; Fig. 1).

Fig. 1 Sensitivity of the TEAM camera-trap protocol, expressed as the number of years of sampling required to detect annual occupancy declines of 15, 10, 5 and 1%, given an effort of 60 or 90 camera traps sampling for 30 days annually, for species with initial occupancy probabilities of 0.1 to 0.9 and detection probabilities of 0.1 to 0.5. Not all declines could be detected within 10 years, particularly small declines (i.e. 1%), which resulted in shorter lines graphed in the figure. Declines that were not detectable within 10 years are shown with points above the dashed line, which demarcates the 10th year.

We estimated the initial occupancy of each of the 511 populations monitored by TEAM using the modelling output of the first global assessment of wildlife trends, which utilized camera-trap data collected during 2007–2014 (Beaudrot et al., 2016). Similarly, we calculated detection probabilities for each population using the same dataset. We defined the number of years required to detect change using a conservative cutoff of an 80%, rather than the typical 95%, confidence interval for classifying occupancy trends, because a wider confidence interval can provide an earlier warning signal of occupancy declines that can prompt conservation action (Myers, 1993). We then used PowerSensor! (2018) to determine the number of years necessary to detect change for each population based on its initial occupancy and detection probabilities and an effort of 60 points with 30 days of sampling.

PowerSensor! displays information that we generated through a simulation and statistical analysis, which we briefly describe here. Firstly, we simulated data for declining species using the dynamic occupancy model formulated by MacKenzie et al. (2003).We generated time series data, varying the following parameters: number of sites, number of times a site is sampled within a survey, occupancy probability in the first survey, detection probability and persistence probability. The colonization probability and the number of surveys were fixed. We intentionally set the colonization probability to zero to simulate population declines as the worst-case scenario. We set the number of surveys to 10 because many biodiversity policy framework plans (e.g. Convention on Biological Diversity) measure progress in 10-year intervals (Butchart et al., 2010). We did not model covariates on initial occupancy, extinction, colonization or detection probability. The parameters did not vary between sites, samples within a survey, or surveys. Once the data were generated, we fitted the same dynamic occupancy model using the colext function of the unmarked package (Fiske & Chandler, 2011) in R 3.5.0 (R Development Core Team, 2016).

Secondly, for each simulation and parameter combination, we fitted the model without covariates and projected the model trajectory under a finite number of sites using the smoothed model projection of unmarked:

$$\hat Z_{k,m,t} = \hat Z_{k,m,t - 1}{\it \Psi} _m,$$

where $\hat Z_{k,m,t}$ is the estimated occupancy from a simulated data set k with parameter combination m at survey t, and ψ is the probability of a site being occupied.

Thirdly, to assess whether the fitted models were able to detect change under a given parameter combination m and after two surveys, we calculated the quantity  $\hat Z_{k,m,1} - \hat Z_{k,m,t}$ for each of the 250 m fitted models and surveys t (t > 1). For each survey t, we obtained a distribution of 250 difference values and tested whether the 80, 90 or 95% confidence intervals of the distribution included the value zero. If so, the model was unable to detect the simulated changes in occupancy for that particular survey given the confidence level. All simulations and analyses were conducted in R, and the code is available on Github  (Ahumada, 2017).

In general, higher rates of decline could be detected more often and within fewer years than lower rates of decline; declines were less detectable when detection probabilities and/or initial occupancy probabilities were low. We found that just 2 years of sampling with 60 camera-trap points was sufficient to detect severe (15%) annual occupancy declines for populations with initial occupancy probabilities ≥ 0.3. For populations with lower initial occupancies (i.e. ψ  =  0.1), severe (15%) declines were generally detectable with 3 years of sampling and 90 camera-trap points.

To detect 10% annual occupancy declines, 2 years of sampling with 60 camera traps was sufficient for populations with initial occupancy probabilities ≥ 0.5. For ψ  =  0.3, 3 years of sampling with 60 camera-trap points was sufficient, and for ψ  =  0.1, 10% declines were detectable with 5 years of sampling and 90 camera-trap points.

For 5% annual occupancy declines the number of years of sampling necessary to detect declines was more contingent on the initial occupancy probability than for 15 and 10% declines. Similarly, the likelihood that declines were detectable was more contingent on the detection probability. Generally, 5% annual declines were detectable with 4 years of sampling using 60 camera-trap points or with 3 years of sampling using 90 camera-trap points for populations with initial occupancy probabilities ≥ 0.3 and detection probabilities ≥ 0.2. Finally, a small (1%) decline was consistently detected within 10 years for detection probability  =  0.5. For initial occupancy ψ  =  0.5 a small decline was detected in 10 years, for initial occupancy ψ  =  0.7 in 6 years, and for initial occupancy ψ  =  0.9 in 5 years.

The majority of the 511 populations that the programme monitors did not meet the initial occupancy probability threshold of 0.1 and detection probability threshold of 0.04 necessary to detect change within 10 years using PowerSensor! (Fig. 2). Specifically, the initial occupancy probabilities for 274 populations (53.6%) were < 0.1 and detection probabilities for 359 populations (70.3%) were < 0.04. We were able to assess the percentage of detectable change for 150 (29.3%) of the 511 populations (Supplementary Table 1). Occupancy changes of 15 and 10% were detectable for all 150 populations within 5 years and 7 years, respectively. Occupancy changes of 5% were detectable for 130 populations within 7 years and changes of 1% were detectable for 80 populations within 10 years. Of these 150 populations, 85.33% were mammals and 14.67% were birds. The majority were herbivores (45.3%) or omnivores (44.0%), and few were carnivores (8.67%) or insectivores (2.0%). According to the IUCN (2014) Red List, the majority of the 150 populations are categorized as Least Concern (76.0%), followed by Vulnerable (8.0%), Near Threatened (5.33%), Endangered (5.33%), Data Deficient (4.67%) and Critically Endangered (0.67%; Supplementary Table 1).

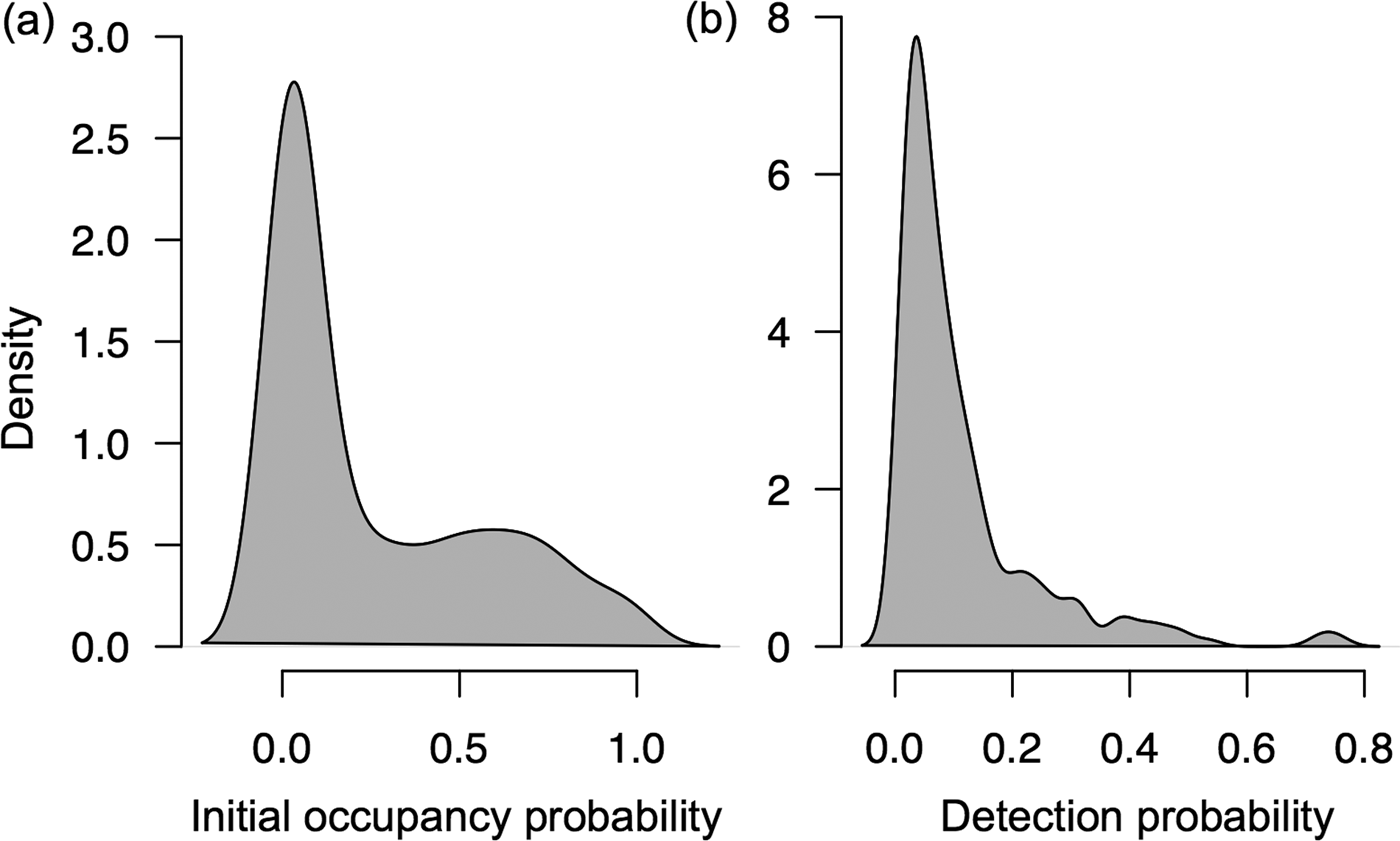
Fig. 2 Density plots of the (a) initial occupancy probabilities (N  =  511 populations) and (b) estimated detection probabilities (N  =  233 populations) for the terrestrial mammal and bird populations that TEAM monitors. The remaining 278 populations had < 5 camera-trap detections per year and therefore had insufficient observations to estimate detection probabilities.

Our examination reveals the relative power and sensitivity of the TEAM protocol to detect annual changes in occupancy given currently available single-species occupancy models for unmarked individuals. The protocol is well suited to detect moderate (≥ 5%) changes in occupancy within 4 years for common tropical species (i.e. initial occupancy > 0.3) that have medium to high detection probabilities (i.e. p > 0.2). The TEAM protocol cannot, however, detect the typical changes in occupancy of rare and evasive species, a category in which most tropical species and many species of conservation concern fall. This is a challenge faced not only by camera trapping but also by many other wildlife monitoring techniques (Ellison & Agrawal, 2005; MacKenzie et al., 2005).

Multi-species models collectively model all species within a community while still allowing each species to respond individually to sampling variables (Dorazio et al., 2006; Zipkin et al., 2009). Such models can provide more precise estimates of occupancy for species that have been observed less often, by formally sharing data across species. To date, multi-species models have been limited in their utility to communities with few rare species or have required the exclusion of the rarest species (Ruiz-Gutierrez et al., 2010). Nevertheless multi-species models may offer a promising method for improving occupancy estimates compared to what is possible with single species models. Additional research is needed to build models for detecting change in rare and elusive species when individuals are unmarked.