No CrossRef data available.
Article contents
Comparative Learning
Published online by Cambridge University Press: 20 October 2023
Abstract
This article concerns the diachronic rationality norms for comparative confidence judgments, that is, judgments of the form “I am at least as confident in 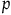 $p$ as I am in
$p$ as I am in 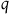 $q$.” Specifically, it identifies, characterizes, and evaluates an intuitively compelling learning rule called comparative conditionalization that specifies how agents should revise their comparative confidence judgments in the face of novel evidence.
$q$.” Specifically, it identifies, characterizes, and evaluates an intuitively compelling learning rule called comparative conditionalization that specifies how agents should revise their comparative confidence judgments in the face of novel evidence.
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of the Philosophy of Science Association
References
Booth, Richard, and Meyer, Thomas. 2011. “How to Revise a Total Preorder.” Journal of Philosophical Logic 40 (2):193–238. https://doi.org/10.1007/s10992-011-9172-8CrossRefGoogle Scholar
Chalmers, David. 2003. “The Content and Epistemology of Phenomenal Belief.” In Consciousness: New Philosophical Perspectives, edited by Smith, Quentin and Jokic, Aleksandar, 220–72. Oxford: Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195311105.003.0009
CrossRefGoogle Scholar
Darwiche, Adnan, and Pearl, Judea. 1997. “On the Logic of Iterated Belief Revision.” Artificial Intelligence 89 (1–2):1–29. https://doi.org/10.1016/S0004-3702(96)00038-0
CrossRefGoogle Scholar
de Finetti, Bruno. 1937. “La prevision: ses lois logiques, ses sources subjectives.” Annales de l’Institut Henri Poincare 7 (1):1–68.Google Scholar
Denoeux, Thierry. 2019. “Decision-Making with Belief Functions: A Review.” International Journal of Approximate Reasoning 109:87–110. https://doi.org/10.1016/j.ijar.2019.03.009
CrossRefGoogle Scholar
Easwaran, Kenny. 2014. “Regularity and Hyperreal Credences.” Philosophical Review 123 (1):1–41. https://doi.org/10.1215/00318108-2366479
CrossRefGoogle Scholar
Eva, Benjamin. 2019. “Principles of Indifference.” Journal of Philosophy 116 (7):390–411. https://doi.org/10.5840/jphil2019116724
CrossRefGoogle Scholar
Eva, Benjamin, and Stern, Reuben. 2022. “Comparative Opinion Loss.” Philosphy and Phenomenological Research. https://doi.org/10.1111/phpr.12921.CrossRefGoogle Scholar
Fagin, Ronald, and Halpern, Jospeh. 1991. “A New Approach to Updating Belief Functions.” In Uncertainty in Artificial Intelligence 6, edited by Piero, P. Bonissone, Henrion, Max, Kanal, Laveen N., and Lemmer, John F., 347–74. Amsterdam: Elsevier.Google Scholar
Fine, Terrence. 1973. Theories of Probability. Cambridge, MA: Academic Press. https://doi.org/10.1016/C2013-0-10655-1
Google Scholar
Fishburn, Peter. 1986. “The Axioms of Subjective Probability.” Statistical Science 1 (3):335–45. https://doi.org/10.1214/ss/1177013611
Google Scholar
Fitelson, Branden, and McCarthy, David. 2014. “Toward an Epistemic Foundation for Comparative Confidence.” http://fitelson.org/cc_handout.pdf.Google Scholar
Forrest, Peter. 1989. “The Problem of Representing Incompletely Ordered Doxastic Systems.” Synthese 79 (2):279–303.CrossRefGoogle Scholar
Freund, Michael. 2005. “Revising Preferences and Choices.” Journal of Mathematical Economics 41 (3):229–51. https://doi.org/10.1016/j.jmateco.2003.11.007
CrossRefGoogle Scholar
Greaves, Hilary. 2006. “Justifying Conditionalization: Conditionalization Maximises Expected Utility.” Mind, 115
(459):607–32. https://doi.org/10.1093/mind/fzl607
CrossRefGoogle Scholar
Halpern, Joseph. 2003. Reasoning about Uncertainty. Cambridge, MA: MIT Press. https://doi.org/10.7551/mitpress/10951.001.0001
Google Scholar
Harrison-Trainor, Matthew, Holliday, Wesley, and Icard, Thomas. 2016. “A Note on Cancellation Axioms for Comparative Probability.” Theory and Decision 80
(1):159–66. https://doi.org/10.1007/s11238-015-9491-2
CrossRefGoogle Scholar
Hawthorne, James. 2016. “A Logic of Comparative Support: Qualitative Conditional Probability Relations Representable by Popper Functions.” In The Oxford Handbook of Probability and Philosophy, edited by Hajek, Alan and Hitchcock, Christopher, 277–95. Oxford: Oxford University Press. https://doi.org/10.1093/oxfordhb/9780199607617.013.13
Google Scholar
Icard, Thomas. 2016. “Pragmatic Considerations on Comparative Probability.” Philosophy of Science 83
(3):348–70. https://doi.org/10.1086/685742
CrossRefGoogle Scholar
Joyce, James. 1998. “A Non-Pragmatic Vindication of Probabilism.” Philosophy of Science 65
(4):575–603. doi:10.1086/392661
CrossRefGoogle Scholar
Joyce, James. 2010. “A Defence of Imprecise Credences in Inference and Decision Making.” Philosophical Perspectives 24
(1):281–323. https://doi.org/10.1111/j.1520-8583.2010.00194.x
CrossRefGoogle Scholar
Kaplan, Mark. 1983. “Decision Theory as Philosophy.” Philosophy of Science 50
(4):549–77. https://doi.org/10.1017/CBO9780511804847
CrossRefGoogle Scholar
Konek, Jason. 2019. “Comparative Probabilities.” In The Open Handbook of Formal Epistemology, edited by Weisberg, Jonathan and Pettigrew, Richard, 267–348. PhilPapers. https://jonathanweisberg.org/pdf/open-handbook-of-formal-epistemology.pdf
Google Scholar
Koopman, Bernard Osgood. 1940. “The Axioms and Algebra of Intuitive Probability.” Annals of Mathematics 41 (2):269–92.CrossRefGoogle Scholar
Kraft, Charles, Pratt, John, and Seidenberg, Abraham. 1959. “Intuitive Probability on Finite Sets.” Annals of Mathematical Statistics 30 (2):408–19.CrossRefGoogle Scholar
Levi, Isaac. 1974. “On Indeterminate Probabilities.” The Journal of Philosophy 71 (13):391–418.CrossRefGoogle Scholar
Levi, Isaac. 1985. “Imprecision and Indeterminacy in Probability Judgment.” Philosophy of Science 52 (3):390–409.CrossRefGoogle Scholar
Lewis, David. 1980. “A Subjectivist’s Guide to Objective Chance.” In Studies in Inductive Logic and Probability, edited by Richard, C. Jeffrey, 263–93. Berkeley: University of California Press.CrossRefGoogle Scholar
Lin, Hanti. 2022. “Bayesian Epistemology.” In Stanford Encyclopedia of Philosophy, Fall 2022 ed., edited by Edward N. Zalta and Uri Nodelman. https://plato.stanford.edu/entries/epistemology-bayesian
Google Scholar
Norton, John. 2021. “Eternal Inflation: When Probabilities Fail.” Synthese 198 (Suppl. 16):S3853–75.CrossRefGoogle Scholar
Raidl, Eric, and Spohn, Wolfgang. 2019. “An Accuracy Argument in Favor of Ranking Theory.” Journal of Philosophical Logic 49 (2):283–313. https://doi.org/10.1007/s10992-019-09518-8
CrossRefGoogle Scholar
Scott, Dana. 1964. “Measurement Structures and Linear Inequalities.” Journal of Mathematical Psychology 1 (2):233–47. https://doi.org/10.1016/0022-2496(64)90002-1
CrossRefGoogle Scholar
Shafer, Glenn. 1976. A Mathematical Theory of Evidence. Princeton, NJ: Princeton University Press. https://doi.org/10.2307/j.ctv10vm1qb
CrossRefGoogle Scholar
Skyrms, Brian. 1985. “Maximum Entropy Inference as a Special Case of Conditionalisation.” Synthese 63 (1):55–74. https://doi.org/10.1007/BF00485955
CrossRefGoogle Scholar
Spohn, Wolfgang. 1988. “Ordinal Conditional Functions: A Dynamic Theory of Epistemic States.” In Causation in Decision, Belief Change, and Statistics II., edited by William, L. Harper and Skyrms, Brian, 105–34 Dordrecht: Kluwer.CrossRefGoogle Scholar
Suppes, Peter. 1994. “Qualitative Theory of Subjective Probability.” In Subjective Probability, edited by Wright, George and Ayton, Peter, 17–37. Hoboken, NJ: Wiley.Google Scholar
Weatherson, Brian. 2007. “The Bayesian and the Dogmatist.” Proceedings of the Aristotelian Society 107 (1):169–85. https://doi.org/10.1111/j.1467-9264.2007.00217.x
CrossRefGoogle Scholar
Williams, Peter. 1980. “Bayesian Conditionalisation and the Principle of Minimum Information.” British Journal for the Philosophy of Science 31 (2):131–44. https://doi.org/10.1093/bjps/31.2.131
CrossRefGoogle Scholar
Wong, S. Michael, Yao, Yiyu, Bollmann, Peter, and Burger, Henning. 1991. “Axiomatization of Qualitative Belief Structure.” IEEE Transactions on Systems, Man and Cybernetics 21 (4):726–34. DOI:10.1109/21.108290
CrossRefGoogle Scholar
Zadeh, Lotfi A. 1978. “Fuzzy Sets as a Basis for a Theory of Possibility.” Fuzzy Sets and Systems 1 (1):3–28. https://doi.org/10.1016/S0165-0114(99)80004-9
CrossRefGoogle Scholar

