Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T04:07:42.550Z Has data issue: false hasContentIssue false
  • English
  • Français

Confirming Power of Observations Metricized for Decisions among Hypotheses

Published online by Cambridge University Press:  14 March 2022

Henry A. Finch
Henry A. Finch*
Affiliation:
The Pennsylvania State University
Get access Rights & Permissions [Opens in a new window]

Abstract

Experimental observations are often taken in order to assist in making a choice between relevant hypotheses ~H and H. The power of observations in this decision is here metrically defined by information-theoretic concepts and Bayes' theorem. The exact (or maximum power) of a new observation to increase or decrease Pr(H) the prior probability that H is true; the power of that observation to modify the total amount of uncertainty involved in the choice between ~H and H: the power of a new observation to reduce uncertainty toward the ideal amount, zero; all these powers are systematically shown to be exact metrical functions of

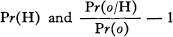
where the numerator is the likelihood of the new observation given H, and the denominator is the “expectedness” of the observation.

Type
Research Article
Information
Philosophy of Science , Volume 27 , Issue 3 , July 1960 , pp. 293 - 307
Copyright
Copyright © 1959 by Philosophy of Science Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

∗∗ Part II of this article will appear in a forthcoming (October, 1960) issue of Philosophy of Science.

1 This essay is dedicated to my colleagues Professor H. B. Curry, and O. Frink, generous sharers of their mastery of logic and mathematics.

2 As will appear below, our proposed explication for “degree of confirmation” or, as we prefer to call it, confirming power differs from previous explications by stressing the importance of rates of change in Pr(H). See for helpful characterization of available explications, Rescher[49].

3 It is consoling to philosophers that mathematicians will sometimes confess concerning the cogency of their own proofs, “Je le vois, mais je ne le crois pas.” See in [43] Cantor to Dedekind, asking for a concurring judgment.

4 I say “Laplacean” form, although Bayes has it quite effectively in his proposition 3 and 5 (00), the latter of which, is nicely proved by Price by “expectation” considerations. Nevertheless Laplace gave currency to the theorem (I) by an explicit provision that the prior probabilities of the alternative hypotheses should not be taken as equal if there is knowledge that they are not, and by freely referring to the probability of causes and the probability of hypotheses as causes [35].

4a In Bayes' splendid memoir, certainly one of the most seminal and important in the history of science, the core problem was to find the chances of judging correctly that the prior probability of an event lies between any two limits one might freely select, given the observation of the frequency of the events occurrence in n experimental trials. First, he examines the logical consequences of the assumption that it is known with what probability the prior probability of an event lies within a sub-interval of the entire interval 0, 1. Then, he examines the logical consequences of the assumption that it is known that the prior probability of the event somewhere on the entire interval, 0, 1. There can be no question that his attempt to solve his core problem for the second main assumption viz. prior probability surely somewhere on the interval as a lemma of his solution of his core problem under the first assumption was a failure. This means only that the kind of estimate he was endeavoring to make cannot be achieved by simple assumptions of equal likelihood in equal intervals for the distribution of the prior probability. Bayes' propositions concerning known fixed or known ranges of prior probabilities are quite sound. Such confusion concerning the import of Bayes' theorem is noticeable in secondary sources that it is necessary to study the original memoir. [1]. Richard Price, the accomplished writer on moral philosophy, strikes a modern note when he writes “... it is certain that we cannot determine in what degree repeated experiments confirm a conclusion...” etc., in his editorial comment.

5 Hence all our results for choice between H and ~H, are easily transformable into results for choice between a null hypothesis H being tested against its logical contrary or contradictory H 1. For an account of the basic logic of such tests see [42].

6 Such a master of the modem ideals of logical rigor as Dedekind has, I remember, written of Bayes' theorem in its relevance to casual heuristic as “eine schöne Theorie” in one of his earlier essays. An admirable elementary exposition of the meaning of Bayes' theorem in its Laplacean form, with good illustrations is to be found in the volume of Gnedenko and Chintschin [22].

7 For the basic paradigm we are considering Carnap's proof is equivalent to the following:

8 Theorem (2) is independent of Pr(o) the expectedness, and therefore is pertinent to an evaluation of the effectiveness of tests for the acceptance or rejection of hypotheses under conditions of various degrees of ignorance concerning the value of Pr(o). See our discussion below in 5 of the theories of Fisher and Neyman-Pearson.

for every true S.

10 By methods similar to those used for theorem (2) it is easily proved that Pr(Ho) ≤ Pr(H*). If H entails o, it is a standard axiom that Pr(o/H) = 1. Hence, when H entails o, Pr(H) ≤ Pr(H*). This wise recommendation of the calculus' own subtlety indicates that o's entailment by H assures against any reduction of Pr(H) by o. Obviously, from (2) a necessary condition for the strengthening of H though an increase in Pr(H) is Pr(o/~H) < 1. This prerequisite is in no manner assured by the entailment of o by H. A rather labored dialectical revelation in stages that entailment of o by H does not suffice to “confirm” H will be found in [24].

10 Kömer's attempted demonstration—which if valid would settle a very crucial issue in epistemology—that it is impossible to judge of the applicability of interpretative concepts by probability measures i.e., impossible to judge that a concept (and hence I take it a conceptual scheme) is probably applicable is in my judgment unsuccessful. Without any critique here of his vague qualitative notion of the difference of intentional meaning, I merely remark that his proof is fragilely suspended on the weak thread of supposition that dependent likelihoods of 1 are sufficient to indicate entailments. Moreover, no one acquainted with living inference in the sciences would, in the slightest, be concerned by the consequences of “attaining” a dependent likelihood of 1 on the basis of any complete stock of evidence; such a perfect likelihood is an ideal which can steadily be approached as a limit; therefore Körner's argument [33a] that the ideal of maximum confirmation cannot be pursued this side of the maximum by successive but unending steps is unconvincing. The situation which would have to occur for Körner's proof to be operative viz. the attainment of Pr(H/all evidence) equals 1 simply does not happen.

11 For an account of the black-raven paradox, presented in such a manner as converts a problem into a mystery, see [24].

12 I am convinced that no science dependent upon observation can make judgments free of probable error; nor is, in my view, measurement required to engender error; counting, ordering, comparing are quite sufficient of themselves. To oppose the belief sometimes countenanced by popular accounts of intuitively-certain discriminations of partial order as a basis of measurement, it is salutory to read Poincaré's account of the endless corrigibility of judgments of identity and difference in the physical continuum [45].

12a I conjecture that one consequence of theorem (2) may be of interest to students of evidence and learning, namely the inequalities (α = Pr(O/H,), β =Pr(O/~H)

Inequality (2a) surely fixes a measure of “stability” for the belief H as it encounters evidence whose character is specifiable by α, β. One might hope too that (2a) could be employed in experimental investigations of the dependence of α, β on the probability of H, for I agree with Ramsey that such dependence upon degree of belief in H is worthy of study.

13 One ought not to assume hastily that Bayes' theorem is indifferent to explanatory power, for what it does actually is to assign a higher probability to a hypothesis precisely because the latter implies observations whose likelihood is greater upon that hypothesis than their prior expectedness. Hypotheses are rewarded precisely because they make observations more expected and calculable. An intellect of the order of Laplace's did not miss the comparison of the probability of hypotheses by the likelihood of observations upon them [31].

13a The asymmetry of the positive and negative portions of the scale defined by (1c) has modern warrant, of course; so penetrating a natural philosopher of our century as Nernst emphasizes that, when experimental observations are in accord with the logical consequences of a hypothesis not directly testable, we have assurance of the acceptability (Brauchbarkeit) but by no means of truth; on the other hand, when experimental observations are not in accord we have assurance not only of non-acceptability but also that there must be something incorrect or untrue (Unrichtigkeit) in our ideas. See Nernet [40].

14 The grand apercu of information theory to be credited I judge ultimately to the magnificent achievements in natural philosophy of Boltzmann [4,6], is that order and organization can be understood as the (comparative) absence of the indeterminateness of entropy. It is more than a metaphor, therefore, to speak of the entropy of a system of choices as a measure of the absence of clear-cut decidability.

15 Since

and

the increment in U′,

However, d(Pr(H) = — d(Pr(~H)), so that we reach, as required, finally.

16 When Pr(H) is greater than ½; every change in U is a decrease in uncertainty as H is strengthened. It is perfectly intelligible however that the rise of Pr(H) from a low initial value may cause an increase of uncertainty by the correlated disconfirmation of ~H until passage through maximum U. Rescher's [49] attention to Pr(H) > ½ is justified.

∗ Part II of this article will appear in a forthcoming (October, 1960) issue of Philosophy of Science.