A learning-based account of local phonological processes

Abstract

Phonological processes tend to involve local dependencies, an observation that has been expressed explicitly or implicitly in many phonological theories, such as the use of minimal symbols in SPE and the inclusion of primarily strictly local constraints in Optimality Theory. I propose a learning-based account of local phonological processes, providing an explicit computational model. The model is grounded in experimental results that suggest children are initially insensitive to long-distance dependencies and that as their ability to track non-adjacent dependencies grows, learners still prefer local generalisations to non-local ones. The model encodes these results by constructing phonological processes starting around an alternating segment and expanding outward to incorporate more phonological context only when surface forms cannot be predicted with sufficient accuracy. The model successfully constructs local phonological generalisations and exhibits the same preference for local patterns that humans do, suggesting that locality can emerge as a computational consequence of a simple learning procedure.

1. Introduction

Phonological processes tend overwhelmingly to involve dependencies between adjacent segments (Gafos 1999; Chandlee et al. 2014). For example, the English plural allomorph depends on the stem-final segment, to which it is adjacent, as in (1).

• 

Moreover, underlying forms are often posited to be minimally different from surface forms, exhibiting abstractness only when surface alternation necessitates it (Kiparsky [1968] 1982; Peperkamp et al. 2006; Ringe & Eska 2013; Richter 2021). This is supported by experimental findings, where children avoid introducing discrepancies between surface and underlying forms when there is little motivation for doing so (Jusczyk et al. 2002; Kerkhoff 2007; Coetzee 2009; van de Vijver & Baer-Henney 2014).

When, and only when, concrete representations are abandoned in favour of (minimally) abstract underlying representations, a child must learn a phonological process to derive the surface form from the abstract underlying form. Experimental studies are revealing about the mechanism underlying sequence learning: humans show a strong proclivity for tracking adjacent dependencies, beginning to track non-adjacent dependencies only when the data overwhelmingly demands it (Saffran et al. 1996, 1997; Aslin et al. 1998; Santelmann & Jusczyk 1998; Gómez 2002; Newport & Aslin 2004; Gómez & Maye 2005). As Gómez & Maye (2005: 199) put it, ‘It is as if learners are attracted by adjacent probabilities long past the point that such structure is useful’. Indeed, artificial-language experiments have repeatedly demonstrated that learners more easily learn local phonological processes than non-local ones (Baer-Henney & van de Vijver 2012) and, when multiple possible phonological generalisations are consistent with exposure data, learners systematically construct the most local generalisation (Finley 2011; White et al. 2018; McMullin & Hansson 2019).

In this article, I hypothesise a mechanistic account of how learners construct phonological generalisations, modelling the learner’s attention as initially fixed locally and expanding farther only when local dependencies do not suffice. The proposed model incorporates the idea that the learning of a phonological process is triggered when, and only when, underlying abstraction introduces discrepancies between underlying and surface representations (Kiparsky [1968] 1982). I view the model’s locally centred attention and default assumption of identity as computationally parsimonious, and thus call it the Parsimonious Local Phonology (PLP) learner. When presented with small amounts of child-directed speech, PLP successfully learns local phonological generalisations. PLP’s search strategy – starting as locally as possible – leads it to accurately exhibit the same preference for local patterns that humans do. Next, I review experimental results on locality in §1.1, the view of learning that PLP adopts in §1.2 and how these reflect principles of efficient computation in §1.3.

1.1. Locality

Early studies of statistical sequence learning found infants to be sensitive only to dependencies between adjacent elements in a sequence. Saffran et al. (1996, 1997) and Aslin et al. (1998) found infants as young as 8 months to be sensitive to dependencies between adjacent elements, while Santelmann & Jusczyk (1998) found that even at 15 months, children did not track dependencies between non-adjacent elements. Studies with older participants revealed that the ability to track non-adjacent dependencies does eventually emerge: adults show a sensitivity to dependencies between non-adjacent phonological segments (Newport & Aslin 2004), and 18-month-old children can track dependencies between non-adjacent morphemes (Santelmann & Jusczyk 1998). However, even as sensitivity to non-adjacent dependencies develops, learners still more readily track local dependencies. Gómez (2002) found that 18-month-olds could track non-adjacent dependencies, but that they only did so when adjacent dependencies were unavailable. Gómez & Maye (2005) replicated these results with 17-month-olds, and attempted to map the developmental trajectory of this ability to track non-adjacent dependencies, finding that it grew gradually with age. At 12 months, infants did not track non-adjacent dependencies, but they began to by 15 months, and showed further advancement at 17 months. These experiments involved a range of elements: words, syllables, morphemes and phonological segments. Moreover, similar results have been observed in different domains, such as vision (Fiser & Aslin 2002). Together, these results suggest that learners might discover only local patterns at early stages in development and that even after sensitivity to less local patterns emerges, a preference for local patterns persists.

Further experiments targeted phonological learning in particular. Subjects in Finley’s (2011) artificial-language experiments learned bounded (local) harmony patterns and did not extend them to non-local contexts when there was no evidence for doing so. However, when exposed to unbounded (non-local) harmony patterns, subjects readily extended them to local contexts. This asymmetry suggests that learners will not posit less local generalisations until the evidence requires it. McMullin & Hansson (2019) replicated these results with patterns involving liquids and with dissimilation. Baer-Henney & van de Vijver (2012) used an artificial-language experiment to test the role of locality (as well as substance and amount of exposure) in learning contextually determined allomorphs. They found that when the allomorph was determined by a segment two positions away, learners more easily acquired and extended the pattern than when the allomorph was determined by a segment three positions away. In short, these studies demonstrate that learners posit the most local generalisation consistent with the data.

1.2. The nature of the learning task

I adopt the view of others (e.g., Hale & Reiss 2008; Ringe & Eska 2013; Richter 2021) that children initially store words concretely, as accurately to what they perceive as their representational capacities allow. As their lexicon grows, surface alternations sometimes motivate the positing of abstract underlying forms, which introduce discrepancies between underlying and surface forms. For example, as Richter (2018, 2021) has characterised in rigorous detail, alternations such as ‘eat’ [] $\sim $ ‘eating’ [] lead to the flap [] and stop [] being collapsed into allophones of underlying /T/. Similarly, a morphemic surface alternation such as ‘cats’ [] $\sim $ ‘dogs’ [] may motivate an abstract underlying plural suffix /-Z/ (or default /-/; Berko 1958). This view is in the spirit of Kiparsky’s ([1968] 1982) Alternation Condition, and has been termed invariant transparency (Ringe & Eska 2013).

A consequence is that when, and only when, concrete segments are collapsed into abstract underlying representations, the need for a phonological grammar arises, to derive the surface forms for abstract underlying forms. I will use the example of stops following nasals to exemplify two significant corollaries. Voiceless stops following nasals are often considered to be a marked sequence, because post-nasal articulation promotes voicing, and post-nasal voicing is typologically pervasive (Locke 1983; Rosenthall 1989; Pater 1999; Hayes & Stivers 2000; Beguš 2016, 2019). Nevertheless, many languages – for example, English – tolerate post-nasal voiceless stops, ¹ and a few even exhibit productive, phonological post-nasal devoicing. For example, Coetzee & Pretorius (2010) performed a detailed experimental study of Tswana speakers, finding that some extended post-nasal devoicing, as in (2), productively to nonce words.

• 

Beguš (2019: 699) found post-nasal devoicing to be reported as a sound change in 13 languages and dialects, and argues that although this pattern appears to operate against phonetic motivation, it likely emerged in each case as the result of a sequence of sound changes that were individually phonetically motivated.

Including a constraint to mark post-nasal voiceless stops in languages that tolerate them makes the learning task unnecessarily difficult, because the constraint must then be downranked despite the absence of surface alternations. Instead, under invariant transparency, children learning languages that tolerate post-nasal voiceless stops will simply not learn a phonological process regarding post-nasal stops, because there is nothing to learn. Moreover, when surface alternations that lack or operate in opposition to phonetic motivation (e.g., post-nasal devoicing) occur synchronically due to diachronic processes or other causes, no serious problem arises: the child simply learns a phonological process to account for the observed alternation, as has been observed in experiments (Seidl & Buckley 2005; Beguš 2018).

The view that children initially hypothesise identity between surface and underlying forms enjoys experimental support. Jusczyk et al. (2002) found that 10-month-old infants better recognise faithful word constructions than unfaithful ones. Van de Vijver & Baer-Henney (2014) found that both 5–7-year-olds and adults were reluctant to extend German alternations to nonce words, preferring instead to treat the nonce SRs as identical to their URs. Kerkhoff (2007) reports a consistent preference for non-alternation in Dutch children aged 3–7 years. In an artificial-language experiment, Coetzee (2009) found that learners more often extend non-alternation than alternation to test words, suggesting that this is learners’ default.

Of course, children’s initial productions are not faithful to adult productions (Smith 1973; Fikkert 1994; Grijzenhout & Joppen 1998; Grijzenhout & Joppen-Hellwig 2002; Freitas 2003), but this is likely due to underdeveloped control of the child’s articulatory system, rather than an early state of the adult grammar (see Hale & Reiss 2008, §3.1 for a detailed argument). For instance, children systematically fail to produce complex CC syllable onsets in early speech even in languages that allow complex onsets, like Dutch, German, Portuguese and English (Fikkert 1994; Grijzenhout & Joppen 1998; Grijzenhout & Joppen-Hellwig 2002; Freitas 2003; Gnanadesikan 2004). Clusters tend to be reduced by deleting a consonant, and development proceeds from a cluster reduction stage to a full CC production stage, suggesting the discrepancy may be due to limited articulatory control.

PLP is a model of how phonological processes are learned once underlying abstraction leads to discrepancies in (UR, SR) pairs, which constitute PLP’s input. As some reviewers of this article pointed out, the task of learning phonological processes to account for discrepancies between underlying and surface forms is intertwined with the task of figuring out when such abstract underlying representations are formed, and what they are like. This is evident when comparing the English plural voicing alternation (e.g., cats [kæts] $\sim $ dogs [dɑɡz]) to the Dutch plural voicing alternation (e.g., [bɛt] ‘bed’ $\sim $ [bɛdәn] ‘beds’; Kerkhoff 2007: 1). English speakers show clear productive, rule-like behaviour (Berko 1958), while Dutch speakers’ generalisation is less clearly rule-like (Ernestus & Baayen 2003; Kerkhoff 2007). The Dutch alternation is obfuscated by its interaction with other voicing alternations such as assimilation (Buckler & Fikkert 2016, §2). Consequently, it may be that the English alternation is systematic enough to drive the learner to systematic underlying abstraction, while the Dutch alternation is not.

Thus, a complete theory of phonological learning must include, in addition to the mechanism by which processes are learned, a precise mechanism characterising how and when abstract underlying forms are posited. For example, Richter (2018, 2021) has hypothesised a mechanism by which learners abandon the null hypothesis of concrete underlying forms in favour of abstraction, and applied it to the case of the English [t] $\sim $ [ɾ] allophones. The results closely matched lexical studies of child utterances, including a U-shaped development curve. Thus, PLP is just one part of the story. However, I believe that this part of the story – learning phonological processes from (UR, SR) pairs – is nevertheless important, and in line with the vast majority of prior work on learning phonological grammars, which have likewise tended to presuppose abstract underlying forms for use in, for example, constraint ranking (Legendre et al. 1990; Boersma 1997; Tesar & Smolensky 1998; Boersma & Hayes 2001; Smolensky & Legendre 2006; Boersma & Pater 2008). ²

1.3. Locality and identity as principles of computational efficiency

Locality and identity have natural interpretations as principles of computational efficiency, or ‘third factors’ (Chomsky 2005; Yang et al. 2017). The more local the context around an underlying segment, the fewer segments the cognitive system need be sensitive to in determining its output (Rogers et al. 2013: 99). Moreover, it is computationally simpler to copy input segments to the output unaltered than to change them in the process.

I present my proposed model in §2, discuss prior models in §3, evaluate the model in §4, and conclude with a discussion in §5.

2. Model: PLP

The proposed model is called PLP, for Parsimonius Local Phonology learner. PLP learns from an input of (UR, SR) pairs, which may grow over time as the learner’s vocabulary expands. It constructs the generalisations necessary to account for which segments surface unfaithfully in those pairs and in what phonological contexts that happens. These generalisations are placed in a grammar, for use in producing output SRs for input URs.

• 

PLP assumes identity between URs and SRs by default: it adds generalisations to only in step (3b-iii), when discrepancies arise. A locality preference emerges from the generalisation strategy it employs in steps (3b-iii-α) and (3b-iv): PLP starts with the narrowest context around an unfaithfully surfacing segment and proceeds further outward from the segment only when an adequate generalisation cannot be found. Consequently, I consider steps (3b-iii-α) and (3b-iv), together with the addition of generalisations to the grammar only when motivated by discrepancies, to be PLP’s main contributions. The code is available on GitHub. ³

2.1. The input

The input to PLP is a set of (UR, SR) pairs, which may grow over time, simulating the learner’s vocabulary growth. As discussed in §1.2, discrepancies between a UR and its corresponding SR arise when a learner abandons concrete underlying representations in favour of underlying abstraction. A discrepancy can be an input segment that does not surface (deletion), an output segment that has no input correspondent (epenthesis) or an input segment with a non-identical output correspondant (segment change). In this work, I treat the (UR, SR) pairs, with discrepancies present, as PLP’s input. Future work will combine this with the important problem of when abstract underlying forms are posited (e.g., Richter 2018). I also assume that the correspondence between input and output segments is known. The same assumption is tacit in constraint ranking models, which use the correspondence for computing faithfulness constraint violations.

The URs and SRs are sequences of segments, which I treat as sets of distinctive features (Jakobson & Halle 1956; Chomsky & Halle 1968). Thus, structuring sound into a phonological segment inventory organised by distinctive features is treated as a separate learning process (e.g., Mayer 2020). I use feature assignments from Mortensen et al. (2016).

I will use the English plural allomorph as a running example. Suppose that at an early stage in acquisition, a child has memorised some of the plural forms of nouns in their vocabulary, as in (4).

• 

At this stage, an empty grammar, which regurgitates each memorised word, will suffice. Moreover, since no discrepancies yet exist, PLP will be content with this empty grammar: the for loop (step (3b-iii)) will not be entered. As the child begins to learn morphology, they may discover the morphological generalisation that plurals tend to be formed by suffixing /-z/. All of the child’s plural URs will then, in effect, be reorganised as in (5).

• 

At this point, when the child goes to use their grammar (step (3b-ii)), they will discover that it now predicts *[kætz] and *[hɔrsz], inconsistent with their expectation based on prior experience with the words. The newly introduced discrepancies trigger the for loop (step (3b-iii)) and require PLP to provide an explanation for them. Suppose the first word to trigger this is //, erroneously predicted as *[kætz] instead of the expected [kæts]. PLP then constructs a generalisation to capture the phonological context in which /z/ surfaces as [s] (step (3b-iii-α)).

2.2. Constructing generalisations

The core component of PLP is its component for constructing generalisations (step (3b-iii-α)).

2.2.1. The structure of generalisations

The generalisations that PLP constructs are pairs , where (6) is a sequence and (7) is an action carried out at a particular position in the sequence. Each element in a sequence is a set of segments from the learner’s segment inventory, (6). ⁴

• 

A set of segments may be extensional, e.g., $s_i =$ {}, or a natural class – e.g., $s_i =$ [ $+$ sib]. An action can be any of those listed in (7): deletion of the ith segment, insertion of new segment(s) to the right of the ith segment, ⁵ or setting the ith segment’s feature f to $+$ or $-$ . ⁶

• 

For example, the generalisation in (8a) states that a consonant is deleted when it follows and precedes other consonants; (8b) says that a schwa is inserted to the right of any sibilant that precedes another sibilant; and (8c) says that the voicing feature of voiced obstruents in syllable-final position is set to $-$ (using $]_{\sigma }$ to indicate the right boundary of a syllable).

• 

Any grammatical formalism capable of encoding these generalisations could be used, but in this article I chose a rule-based grammar. The specified set of possible actions is meant to cover a majority of phonological processes, but more could be added if necessary (e.g. metathesis).

The part of the sequence picked out by the index i determines the target of the rule, and the part of the sequence to the left and right of i determine the rule’s left and right contexts. Each type of action (7) can be encoded in one of the rule schemas in (9), where .

• 

Thus, the generalisations in (8) are encoded as the rules in (10).

• 

Each sequence in is strictly local (McNaughton & Papert 1971) – describing a contiguous sequence of segments (see Appendix A for elaboration) – and has the same structure as the ‘sequence of feature matrices’ constraints from Hayes & Wilson (2008: 391). Moreover, the input–output relations described by each generalisation are probably ⁷ input strictly local maps (Chandlee 2014). These structures are not necessarily capable of capturing all phonological generalisations, and intentionally so. Typological considerations point to strict locality as a central property of generalisations, due to its prevalence (Chandlee 2014) and repeated occurrence across representations (Heinz et al. 2011). This article is intentionally targeting precisely those generalisations, and I discuss principled extensions for non-local generalisations in §5.2.

2.2.2. Searching generalisations

When PLP encounters a discrepancy – an input segment surfacing unfaithfully – it uses the algorithm in (11) to construct a generalisation . I refer to the discrepancy as , where x is the input segment and $y \neq x$ is its surface realisation. ⁸

• 

PLP uses a window, , to control the breadth of its search. The window is a sequence of cells that can be filled in to create ’s sequence (6). The window starts with only one cell, filled with $s_0 = \{x\}$ (step (11a)). PLP then infers the type of change from x to y as in (12).

• 

For Ins, the value inserted () is y; for Set, the featured changed (f) and its value ( $+$ or $-$ ) are inferred from the difference between x and y. The index i specifies where x falls in ’s sequence, ; initially, since , $i = 1$ (step (11b)).

As Figure 1a visualises, PLP starts with the most local generalisation, which makes no reference to the segment’s context: the segment always surfaces unfaithfully. In the running example, PLP first posits (13), which predicts that /z/ always surfaces as [s] (Figure 1b).

• 

Figure 1 (a) The width of PLP’s search expands outward (upward arrows) when and only when an adequate generalisation cannot be formed from a narrower context. (b) and (c) An example of PLP on seven English plural nouns. (b): PLP’s first generalisation (13) is based on only the alternating segment and makes too many wrong predictions; this triggers PLP to expand its attention window. (c) PLP then forms generalisation (15a), which is based on the left-adjacent segment and allows the /z/ $\to $ [s] instances to be isolated.

This, however, is contradicted by other words in the vocabulary: /z/ surfaces faithfully as [z] in words like [] and with an epenthetic vowel in words like [], which suggests that this initial generalisation is wrong (step (11c)) and that the breadth of the search must be expanded (Figure 1a).

2.2.3. When to expand breadth of search

To come to such a verdict, PLP computes the number of predictions the rule makes over the current vocabulary and how many of those are correct. The number of predictions (13) makes is the number of times /z/ appears in the learner’s vocabulary, and those that surface as [s] are the correct predictions. There are a number of options for determining the adequacy of the generalisation. We could require a perfect prediction record, but this may be too rigid due to the near inevitability of exceptions in naturalistic data. More generally, we could place a threshold on the number or fraction of errors that the generalisation can make. The choice of criterion does not substantially change PLP: going from local generalisations to less local ones proceeds in the same way regardless of the quality criterion, which simply determines the rate at which the more local generalisations are abandoned. In this work, PLP uses the Tolerance Principle (Yang 2016) as the threshold, which states that a generalisation making predictions about what an underlying segment surfaces as is productive – and hence the while loop (step (11c)) can be exited – if and only if the number of incorrect predictions it makes (called for exceptions) satisfies (14).

• 

The threshold is cognitively motivated, predicting that children accept a linguistic generalisation when it is cognitively more efficient to do so (see Yang 2016, ch. 3 for how this threshold is identified). Since the threshold is based on cognitive considerations and has had success in prior work (e.g., Schuler et al. 2016; Koulaguina & Shi 2019; Emond & Shi 2021; Richter 2021; Belth et al. 2021), it is a reasonable choice for this article. In the current example, (13) has and , which fails the criterion in (14): $4> \frac {7}{\ln 7} (\approx 3.6)$ . Thus, the while loop in (11c) is entered.

2.2.4. Expanding breadth of search

Once the initial hypothesis that /z/ always surfaces as [s] is ruled out as too errant, PLP adds one cell to the window (step (11c-i)). PLP fills the window with the sequence that matches the fewest of the sequences where /z/ does not surface as [s]. In other words, it chooses the context that better separates words like // from words like // and //. Thus, for the vocabulary in Figure 1b and 1c, PLP prefers (15a) over (15b) because a left context of {} is more successful than a right context of {#} at distinguishing the places where /z/ does indeed surface as [s] from those where it does not. ⁹ That is, PLP chooses the rule with the most accurate context fitting in the current window, where accuracy is measured as the fraction of the rule’s predictions over the training URs that match the corresponding training SRs. In our example, then, PLP’s second hypothesis is that /z/ surfaces as [s] whenever it follows a //, //, or //.

• 

Figure 1a visualises PLP’s search: it hypothesises a context where an underlying segment surfaces as some particular segment other than itself, checking whether the hypothesis is satisfactorily accurate, and expanding the breadth of its search if not. This process halts once a sufficiently accurate hypothesis has been discovered.

2.3. Encoding generalisations in a grammar

The generalisations that PLP constructs are encoded in a grammar to be used in producing an SR for an input UR. The grammar, , consists of a list of rules. Each time PLP constructs a generalisation (step (3b-iii-α)), it is placed in the appropriate rule schema (9) and added to the list of rules. If PLP replaces a generalisation due to underextension or overextension (step (3b-iv)), as described in §2.4, the old, offending rule is removed and a new one added. §2.3.1 discusses how rules that carry out the same action are combined; §2.3.2 discusses how natural classes are induced; §2.3.3 discusses how the list of rules is ordered and §2.3.4 discusses how produces outputs from inputs.

2.3.1. Combining generalisations

Generalisations that carry out the same change over different segments are combined in the grammar, so long as the resulting rule is accurate to a degree that satisfies the criterion in (14). For instance, the three rules in (16a) would be grouped into the single rule (16b).

• 

2.3.2. Inducing natural classes

Up to this point, PLP’s generalisations have been over sets of particular segments. Humans appear to generalise from individual segments to natural classes, as has been recognised by theory (Chomsky & Halle 1965; Halle 1978; Albright 2009) and evidenced by experiment (Berent & Lennertz 2007; Finley & Badecker 2009; Berent 2013).

PLP thus attempts to generalise to natural classes for each set of segments in a generalisation’s sequence , in terms of shared distinctive features (Jakobson & Halle 1956; Chomsky & Halle 1968). The procedure can be thought of as retaining only the features shared by segments in needed to keep the rule satisfactorily accurate. To exemplify this part of the model, I will assume PLP has constructed the epenthesis rule in (17), which produces mappings such as // $\rightarrow $ [].

• 

The procedure, outlined in (18), starts with a new sequence of length , with each element an empty natural class (step (18a)).

• 

For the rule in (17), the sequence is (19a) and the (empty) initial natural class sequence is (19b). Each element of can take any feature shared by the corresponding segments in , so the set of feature options is (19c), which includes elements like ( $+$ sib, 1) because {} share ‘ $+$ sib’ as a feature and ( $+$ voi, 2) because {} has ‘ $+$ voi’ as a feature, but it does not include ( $+$ voi, 1) because {} do not agree in this feature.

• 

In the while loop (step (18c)), features are added one at a time to , choosing at each step the feature from (19c) that best narrows the extension of (initially all sequences of length ) to those in the extension of (which is {}). Thus, adding the feature ‘ $+$ sib’ to the first natural class (20a) will narrow ’s extension towards ’s better than ‘ $+$ cons’. As before, the new generalisation is evaluated according to the Tolerance Principle threshold in (14). In the current example, (20a) will still have sequences like {} in its extension, so ‘ $+$ sib’ will then be added to the second natural class (20b).

• 

This new sequence, , still has an extension greater than the original . However, because adjacent sibilants are indeed disallowed in English, this inductive leap is possible, and thus (17) will be replaced with (21) in the grammar.

• 

This differs from the natural class induction in Albright & Hayes (2002, 2003), which generalises as conservatively as possible by retaining all shared features (see §B.4).

It may be possible for natural class induction to influence rule-ordering, so PLP identifies natural classes before determining the order in which the rules should apply. Specifically, natural classes are induced with rules temporarily ordered by scope (narrowest first), before the final ordering is computed as in §2.3.3.

2.3.3. Rule ordering

In some cases, phonological processes may interact, in which case the interacting rules may need to be ordered. The topic of rule interaction and ordering has received immense attention in the literature – especially in discussions of opacity – and extends well beyond the scope of the current article. However, I will summarise PLP’s approach to rule ordering, and characterise the path to a more systematic study of PLP’s handling of complex rule interactions.

The standard rule interactions discussed in the literature are feeding, bleeding, counterfeeding and counterbleeding, described in (22) following McCarthy (2007) and Baković (2011).

• 

Counterfeeding and counterbleeding are counterfactual inverses of feeding and bleeding: if $r_j$ counterfeeds (or counterbleeds) $r_i$ , it would feed (or bleed) $r_i$ if it preceded $r_i$ . McCarthy’s (2007, §5.3) example of feeding, reproduced in (23), comes from Classical Arabic, where vowel epenthesis before word-initial consonant clusters ( $r_i$ ) feeds [] epenthesis before syllable-initial vowels ( $r_j$ ).

• 

McCarthy (2007, §5.4) also provides an example of counterfeeding. In Bedouin Arabic, short high vowels are deleted in non-final open syllables, and // is raised in the same environment. However, as (24) shows, because deletion precedes raising, the raising of the short vowel // to [] does not feed deletion.

• 

Examples of bleeding and counterbleeding come from dialects of English where // and // are flapped – [] – between stressed and unstressed vowels, while // and // raise to [] and [] before voiceless segments. The canonical case is counterbleeding order, where raising occurs before underlying // even when it surfaces as voiced [] on the surface, as in (25).

• 

In less-discussed dialects of English in Ontario (Joos 1942) and in Fort Wayne, Indiana (Berkson et al. 2017), the flapping of voiceless // as voiced [] bleeds raising as in (26).

• 

Given two interacting rules $r_i$ and $r_j$ , it is straightforward to order them by following standard arguments. Specifically, ordering $r_i$ before $r_j$ (feeding/bleeding order) will produce errors on data from a language where $r_j$ in fact precedes $r_i$ (counterfeeding/counterbleeding) and vice versa. For example, if we call English dialects where flapping counterbleeds raising (25) ‘Dialect A’ and the dialects with bleeding (26) ‘Dialect B’ (following Joos 1942), ordering flapping before raising in Dialect A will erroneously cause // to surface as [] instead of []. Consequently, the correct counterfeeding order will yield higher accuracy than feeding order for a leaner exposed to Dialect A. A symmetrical argument holds for ordering in Dialect B.

Thus, for each pair of learned rules, PLP chooses the pairwise ordering with higher accuracy. To yield a full ordering of the rules, PLP constructs a directed graph where each rule in forms a node. PLP considers each pair of rules and places a directed edge from $r_i$ to $r_j$ iff the accuracy of $r_j \circ r_i$ (i.e., applying $r_i$ first and $r_j$ to its output) is greater than that of the reverse, $r_i \circ r_j$ . The directed graph is then topologically sorted to yield a full ordering. ¹⁰ Rules that interact are assigned the order that achieves higher accuracy, and non-interacting rules are ordered arbitrarily.

The bigger challenge is the possibility that the interactions between $r_i$ and $r_j$ obfuscate the independent existence of the rules, thereby making it difficult for them to be discovered in the first place. Counterfeeding and counterbleeding present no issues, because applying each rule independently, directly over the UR, produces the same SR as applying them sequentially in counterfeeding/counterbleeding order. For example, in McCarthy’s (2007) Bedouin Arabic example in (24), // $\rightarrow $ [] is accounted for by the raising rule, and there is no deletion in // $\rightarrow $ [] to hinder the discovery of the deletion rule. Similarly, the // $\rightarrow $ [] discrepancy in (25) can be accounted for by raising without reference to flapping, and the // $\rightarrow $ [] discrepancy can be accounted for by flapping without reference to raising. I give an empirical demonstration of PLP learning rules in counterbleeding order in §4.3.4.

Since bleeding destroys contexts where a rule would have applied, it can cause overextensions. For example, when PLP is attempting to construct a raising rule for (26), the rule in (27) (treating the diphthong as a single segment) would overextend to //.

• 

However, since PLP allows some exceptions in accordance with the Tolerance Principle, this will only matter if the bled cases are pervasive enough to push the rule over the threshold in (14). Whether this happens must be determined on a case-by-case basis by the learner’s lexicon. If the threshold of exceptions is crossed, PLP will simply expand the width of its search. When flapping bleeds raising (26), raising occurs distributionally before underlying voiceless segments that are not between a stressed and an unstressed vowel. The latter condition describes the contexts where raising is not bled, and still falls within a fixed-size window of the raising target, such as the underlined portion of //. The general point here is that if two rules interact extensively, there is still likely to be a fixed-length context – possibly a slightly larger one – that accounts for the processes. In fact, Chandlee et al. (2018) have shown that a wide range of phonological generalisations characterised as opaque in the literature can be formalised as input strictly local maps. In Appendix A, I show that the rules PLP learns correspond to Input Strictly Local maps. Thus, I am optimistic that PLP can succeed even with instances of opaque rule interactions. §4.4 provides an empirical demonstration of PLP learning rules in bleeding order.

Feeding may require small adaptions to PLP. In (23), no issue arises for the vowel-epenthesis rule, which does the feeding. The search for a rule to account for epenthetic [] will proceed analogously to the bleeding case. There are two underlying environments where epenthetic [] surfaces: before underlyingly initial vowels (# _ _ V) and before underlying initial consonant clusters (i.e., where raising feeds epenthesis, # _ _ CC). These are disjoint contexts, so it may be appropriate to adapt PLP to allow it to return two disjoint rules from its search in (11) to account for a discrepancy. In that case, the rules in (28) account for ʔ-epenthesis directly from URs.

• 

Alternatively, PLP could be adapted such that the search for new generalisations (step (3b-iii-α)) operates over intermediate representations – specifically those derived by existing rules – instead of underlying representations. In that case, the ʔ-epenthesis rule could be directly learned over the intermediate forms derived by the vowel-epenthesis rule.

In summary, this article is not an attempt to provide a complete account of rule ordering, which is beyond its scope. The results in §4.3.4 and §4.4 provide empirical demonstration of PLP learning some interacting rules, and the above discussion provides an outline of how PLP approaches rule interaction and what extensions may be necessary.

2.3.4. Production

The rules are applied one after another in the order produced by the procedure in §2.3.3. Each individual rule is interpreted under simultaneous application (Chomsky & Halle 1968), which means that when matching the rule’s target and context, only the input is accessible, not the result of previous applications of the rule. Thus, following the example from Chandlee et al. (2014: 37), the rule in (29) applied simultaneously to the input string $aaaa$ yields the output $abba$ rather than $abaa$ , because the second application’s context is not obscured by the first application.

• 

Simultaneous application is the interpretation of rules that corresponds to input-strictly local maps, as discussed in §A.2. Other types of rule application, such as iterative or directional (e.g., Howard 1972; Kenstowicz & Kisseberth 1979), could be used in future work.

Thus, for an input u and ordered list of rules , the grammar’s output $\hat {s}$ is given by the composition of rules in (30).

• 

2.4. Updating incrementally

As PLP proceeds, vocabulary growth may cause the grammar to become stale and underextend or overextend, at which point PLP updates any problematic generalisations (step (3b-iv)).

Denoting the discrepancies between the input and the predicted output as , and those between and as , underextensions are defined in (31a) as discrepancies between the input and expected output that are not accounted for in PLP’s prediction , and overextensions are defined in (31b) as discrepancies in the predicted output that should not be there. Here the symbol $\setminus $ denotes set difference, and $\triangleq $ means ‘equals by definition’.

• 

Underextensions are handled by the for loop (step (3b-iii)). Inside the loop, a new generalisation is created (step (3b-iii-α)). This is encoded in the grammar (step (3b-iii-β)) by adding it to this list of rules. If a prior generalisation for the discrepancy exists, it is deleted from the list. An example of this is (32), where the word // (32b) freshly enters the vocabulary.

• 

Prior to its arrival, the rule (33a) was sufficient to explain when /z/ surfaces as [s]. This, however, fails to account for the new word, which ends in // not //. PLP handles this by discarding the old rule and replacing it with a fresh one, such as (33b), derived by the same process described above in §2.2.

• 

Overextension – a discrepancy between the input and PLP’s prediction that did not exist between and the expected output – is handled by (step (3b-iv)). An example is (34), where (34b) enters the learner’s vocabulary after (34a).

• 

In such a case, the rule in (35) will have been sufficient to explain (34a), but will result in an erroneous *[] for (34b).

• 

PLP resolves this by discarding the previous rule and replacing it with a new one by the process in §2.2.

For both underextension and overextension, when the list of rules is updated, the steps in §2.3 – combining generalisations, inducing natural classes and ordering rules – are repeated. Since PLP can replace generalisations as needed as the vocabulary grows, it can learn incrementally, in batches, or once and for all over a fixed vocabulary.

3. Prior models

3.1. Constraint-based models

Constraint-ranking models rank a provided set of constraints. Tesar & Smolensky’s (1998) Constraint Demotion algorithm was an early constraint-ranking model for OT. Others are built on stochastic variants of OT or Harmonic Grammar (HG; Legendre et al. 1990; Smolensky & Legendre 2006), including the Gradual Learning Algorithm (Boersma 1997; Boersma & Hayes 2001) for Stochastic OT and a later model (Boersma & Pater 2008) that provided a different update rule for HG (see Jarosz 2019 for an overview).

Constraint-ranking models can capture the assumption of classical OT that learning amounts to ranking a universal constraint set, or they can rank a learned constraint set. Hayes & Wilson’s (2008) Maximum Entropy model learns and ranks constraints, but it learns phonotactic constraints over surface forms, not alternations as PLP does.

Locality and identity biases are better reflected in the content of the constraint set than in the constraint ranking algorithm. Locality is determined in virtue of what segments are accessed in determining constraint violations.

Constraint-ranking models usually begin with markedness constraints outranking faithfulness constraints (Smolensky 1996; Tesar & Smolensky 1998; Jusczyk et al. 2002; Gnanadesikan 2004). Consequently, any UR will initially undergo any changes necessary to avoid marked structures, even in the absence of surface alternations that would motivate discrepancies. Ranking faithfulness constraints above markedness constraints has been advocated by Hale & Reiss (2008), but this approach has not been widely adopted. This in part due to arguments that such an initial ranking would render some grammars unlearnable (Smolensky 1996), and in part due to the view that features of early child productions, in particular ‘emergence of the unmarked’, reflect an early stage of the child’s grammar, rather than underdeveloped articulatory control.

3.2. Rule-based, neural network, and linear discriminative models

Johnson (1984) proposed an algorithm for learning ordered rules from words arranged in paradigms as a proof of concept about the learnability of ordered-rule systems. This algorithm does not incorporate a locality bias and has not been extensively studied empirically or theoretically.

Albright & Hayes (2002, 2003) developed a model for learning English past tense morphology through probabilistic rules. The model can be applied to learn rules for any set of input–output word pairs, including phonological rules. It is called the Minimum Generalisation Learner, because when it seeks to combine rules constructed for multiple input–output pairs, it forms the merged rule that most tightly fits the pairs. A consequence of this generalisation strategy is that the phonological context of the rule is as wide as possible around the target segment, only localising around the target when less local (and hence less general) contexts cannot be sustained. This is the direct opposite of PLP and of experimental results that suggest human learners start with local patterns and move to non-local patterns only when local generalisations cannot be sustained (Finley 2011; Baer-Henney & van de Vijver 2012; McMullin & Hansson 2019). I further discuss differences between PLP and Minimal Generalisation Learner (MGL) in Appendix B.

Rasin et al. (2018) propose a Minimum Description Length model for learning optional rules and opacity. The authors intended the model as a proof of concept and only evaluated it on two small artificial datasets.

Peperkamp et al. (2006) propose a statistical model for learning allophonic rules by finding segments with near-complementary distributions. The method is not applicable to learning rules involving non-complementary distributions. Calamaro & Jarosz (2015) extend the model to handle some cases of non-complementary distributions, if the alternation is conditioned by the following segment (i.e., $a \rightarrow b / \_\_\ c$ where $|a| = |b| = |c| = 1$ ). These works attempt to model the very early stage of learning alternations (White et al. 2008) prior to most morphological learning, whereas PLP models learning after abstract URs have begun to be learned.

Beguš (2022) trained a generative, convolutional neural network on audio recordings of English-like nonce words, which followed local phonological processes and a non-local process (vowel harmony). The model was then used to generate speech. This model-generated speech followed the local processes more frequently than the non-local process, suggesting that it more easily learned local than non-local processes. This is possibly due to the use of convolution, which is a fundamentally local operation. As a model for generating artificial speech, it is not directly comparable in the context of learning processes that map URs to SRs.

In a different direction, Baayen et al. (2018, 2019) propose using Linear Discriminative Learning to map vector representations of form onto vector representations of meaning and vice versa. Since this model operates over vector representations of form and meaning, it is not directly comparable.

3.3. Formal-language-theoretic models

Formal-language- and automata-theoretic approaches analyse phonological generalisations in computational terms. Many resulting learning models attempt to induce a finite-state transducer (FST) representation of the map between SRs and URs. These automata-theoretic models, together with precise assumptions about the data available for learning, allow for learnability results in the paradigm of identification in the limit (Gold 1967). Such results state that a learning algorithm will converge on a correct FST representation of any function from a particular family, provided that the data presented to it meet certain requirements – called a characteristic sample. In phonology, the target class of functions is usually one that falls in the sub-regular hierarchy (Rogers et al. 2013), which contains classes of functions more restrictive than the regular region of the Chomsky Hierarchy (Chomsky 1959). These models are often chosen to demonstrate theoretical learnability results, and have seldom been applied to naturalistic data.

Gildea & Jurafsky (1996) developed a model, based on OSTIA (Oncina et al. 1993), which learns subsequential FSTs. The class of subsequential functions is a sub-regular class of functions that may be expressive enough to capture any type of observed phonological map (Heinz 2018), although some tonal patterns appear to be strong counterexamples (Jardine 2016). The authors intended their model only as a proof of concept of the role of learning biases, and it requires unrealistic quantities of data to learn effectively. Indeed, the authors recognise the importance of faithfulness and locality as learning biases, which they attempted to embed into OSTIA. Their biases were, however, heuristics. In particular, a bias for locality was introduced by augmenting states with the features of their neighbouring contexts. This in effect restricts the learner to local patterns, which is different from the current article’s proposal, in which locality is a consequence of how the algorithm proceeds over hypotheses.

As Chandlee et al. (2014) observes, a more principled means of incorporating a locality bias into a finite-state model is to directly target the class of strictly local functions. Chandlee et al. (2014) propose such a model, called ISLFLA, and prove that it can learn any strictly local function in the limit, in the sense of Gold (1967). However, the characteristic sample for the algorithm includes the set of input–output pairs for every language-theoretically possible string up to length k (a model-required parameter). As Chandlee et al. (2014) discusses, this is problematic, since natural language may in principle never provide all logically possible strings, due to phonotactic or morophological constraints. I implemented ISLFLA and attempted to run it on naturalistic data, and it does indeed fail to identify any FST on such data. ¹¹

Jardine et al. (2014) propose a model, SOSFIA, for learning subsequential FSTs when the FST structure is known in advance; only the output for each arc in the FST needs to be learned. Strictly local functions are such a case, because the necessary and sufficient automata-theoretic conditions of strict locality include a complete FST structure (Chandlee 2014). SOSFIA also admits learnability in the limit results but has not been applied to naturalistic data.

4. Evaluating the model

This section evaluates PLP, addressing the questions listed in (36):

• 

4.1. Model comparisons

I compare PLP to several alternative models.

4.1.1. Rule-based, neural network and finite-state models

MGL is the Minimal Generalisation Learner from Albright & Hayes (2002, 2003). I used the Java implementation provided by the authors. MGL may produce multiple candidate SRs for a UR if more than one rule applies to the UR. In such cases, I used the rule with the maximum conditional probability scaled by scope (confidence in the terminology of Albright & Hayes 2002, §3.2) to derive the predicted SR.

ED (encoder–decoder) is a neural network model. It is a successful neural network model for many natural language processing problems involving string-to-string functions, such as machine translation between languages (Sutskever et al. 2014) and morphological reinflection (Cotterell et al. 2016). It has also been used to revisit the use of neural networks in the ‘past tense debate’ of English morphology (Kirov & Cotterell 2018), though its use as a computational model of morphological acquisition has been called into question (McCurdy et al. 2020; Belth et al. 2021). I follow Kirov & Cotterell (2018) and Belth et al. (2021) in its setup, using the same RNN implementation, trained for 100 epochs, with a batch size of 20, optimising the log-likelihood of the training data. Both the encoder and the decoder are bidirectional long short-term memory networks (LSTMs) with 2 layers, 100 hidden units, and a vector size of 300.

OSTIA (Oncina et al. 1993) is a finite-state model for learning subsequential finite-state transducers. I used the Python implementation from Aksënova (2020).

ID is a trivial baseline that simply copies every input segment to the output. This allows for interpreting the value of assuming UR–SR identity by default.

4.1.2. Learning as constraint ranking

I also compare PLP to the view of learning as ranking a provided constraint set. Classic OT views constraints as part of UG; I represent this view with Ucon , for universal constraint set. An alternative view is that the constraint set is learned; I represent this view with Oracle , which effectively constitutes an upper bound on how well a model that learns the constraint set to be ranked could do. Oracle is provided with all and only the markedness constraints relevant to the grammar being learned. Ucon is provided with the same constraints as Oracle, plus two extra markedness constraints that are violable in the adult languages and thus must be downranked.

It is important to emphasise that these models learn in a different setting from PLP and those in §4.1.1. The latter receive as input only UR–SR training pairs, whereas Ucon and Oracle receive both training pairs and a constraint set. Consequently, Ucon and Oracle’s accuracy levels in producing SRs are not directly comparable to those of other models. My goal in comparing PLP to Ucon and Oracle is to highlight how PLP’s account of phonological learning differs from theirs.

For Ucon and Oracle, I use the Gradual Learning Algorithm (GLA; Boersma 1997; Boersma & Hayes 2001) to rank the constraints, because it is robust to exceptions – an important property when learning from noisy, naturalistic data. I emphasise, however, that the comparison is not to the particular constraint-ranking algorithm; others could have been chosen. Because the experiments involve many random samples and tens of thousands of tokens, the implementation of GLA in Praat (Boersma 1999) was not well-suited. Thus, I used my own Python implementation of GLA, with the same default parameters as in Praat (evaluation noise: 2.0, plasticity: 1.0). I initialise markedness constraints above faithfulness constraints.

4.2. Comparison to humans’ preference for locality

In an experimental study, Baer-Henney & van de Vijver (2012) found that allomorphic generalisations in an artificial language were more easily and successfully learned when the surface allomorph was determined by a segment two positions away than when it was determined by a segment three positions away. The study involved three artificial languages in which plural nouns were formed by affixing either the [ $-$ back] vowel [-y] or its [ $+$ back] counterpart [-u]. Each language involved a different phonological condition for determining which affix surfaced. Treating /-/ as the underlying affix, the three generalisations are those in (37).

• 

All singular forms are CVC words; plurals add a vowel. The (37a) language is an example of vowel harmony, since the affix vowel assimilates in backness to the preceding vowel. The (37b) language is equally local, but lacks clear phonetic motivation, since the stem vowel feature that determines the affix’s backness is [tense]. The (37c) language is both less local and phonetically unmotivated, since the backness of the suffix vowel is determined by the initial consonant of the stem. Because all three languages have CVC stems and CVCV plurals, each pattern is strictly local, but (37a) and (37b) each involve a sequence of three contiguous segments, while (37c) involves four.

Since PLP starts locally around the affix when looking for an appropriate generalisation, and only proceeds outward when the more local contexts become too inaccurate, I expect PLP to learn the (37a) and (37b) generalisations substantially more easily than the (37c) generalisation, just as Baer-Henney & van de Vijver (2012) found for humans (Q3). For comparison, I use MGL, which generalises in roughly the opposite way: it constructs the narrowest – and hence less local – generalisation. I also compare to grammars resulting from ranking three different constraint sets. The markedness constraints for (37) are listed in (38).

• 

The first constraint set encodes the assumption of a universal constraint set containing only grounded, universal constraints by including only (38a), because it is the only generalisation viewed as phonetically motivated. Second, I consider a constraint set containing all three markedness constraints in (38) regardless of which language is being learned. Third, I consider a constraint set containing only the constraint relevant to the language being learned.

Baer-Henney & van de Vijver (2012) found not only that the local generalisations were learned more easily than the non-local one, but also that the phonetically motivated generalisation (37a) was learned slightly more easily than (37b). The authors argued that this is evidence for substantive bias in phonological learning. However, the question of substantive bias is largely orthogonal to the current article, since my focus is on locality. Moreover, the performance gap between (37a) and (37b) was much smaller than the gap between them and (37c). For these reasons, I focus on the difference in models’ performance on (37a,b) vs. (37c) in this experiment.

4.2.1. Setup

Each of Baer-Henney & van de Vijver’s (2012) experiments involved presenting subjects with randomly selected singulars and plurals from the respective artificial languages. Each word was accompanied by a picture conveying the word’s meaning; one item was present in the picture for singulars and multiple items for plurals. The singulars and plurals were presented independently, so the experimental setup did not separate phonological learning from learning the artificial languages’ morphology and semantics. Because of this, the study participants likely only successfully acquired the underlying and surface representations for a subset of the exposure words, and what fraction of the exposure set they learned is entirely unknown. Since the models assume URs and SRs as training data, I factor out the fraction of the exposure set for which they have acquired URs and SRs by treating it as a free variable that the models can optimise over. I use the data released by Baer-Henney & van de Vijver (2012) and follow their setup to construct training (exposure) and test sets. ¹² I ran each model over 100 randomised exposure sets to simulate 100 participants.

The MGL model from Albright & Hayes (2002, 2003) combines rules that target the same segment and carry out the same change to that target. For instance, if it has acquired the two word-specific rules in (39a) and (39b), it will attempt to combine them through Minimal Generalisation – that is, as conservatively as possible. The minimal generalisation for (39a) and (39b) is (39c), which retains as much as possible of the original two rules. However, in the implementation of MGL from Albright & Hayes (2002, 2003), when two rules are combined, the longest substrings shared by the rules are retained – in this case // – but segment combination (e.g., {}) proceeds only one position further; everything else is replaced by a free variable X (see Albright & Hayes 2002: 60 for a complete description of this process). Thus, their implementation returns (39d), which is less conservative than the actual minimal generalisation (39c).

• 

This issue does not arise in the original articles by Albright & Hayes (2002, 2003), because the object of study was the English past tense, in which the surface allomorph is determined by an immediately adjacent segment. Thus, any regularities beyond the adjacent segment, which their implementation would miss, would be spurious anyway. However, for the purposes of this experiment, the implementation is problematic. Consequently, I used my own implementation of MGL, which correctly generates the minimally general combination of rules. ¹³ I use the rule with the minimally general context in which /-/ surfaces as [-] to produce a surface form for each test instance.

4.2.2. Results

Figure 2 shows the results. The x-axis of each plot is the free variable discussed above, measuring the fraction of the exposure set that the learner successfully constructed a UR–SR pair for. The y-axis reports the average model performance (over the 100 simulations) for each language. The points marked with a colour-coded $\times $ provide the average performance over the 20 human participants from Baer-Henney & van de Vijver (2012). Since each model gets to optimise over the free variable, I select, for each respective model, the x-value where it best matches the human performance, averaged over all three languages. This point can be seen by where the $\times $ marks are placed. A colour-coded vertical line from each human performance marker to the corresponding model performance shows the difference between the two.

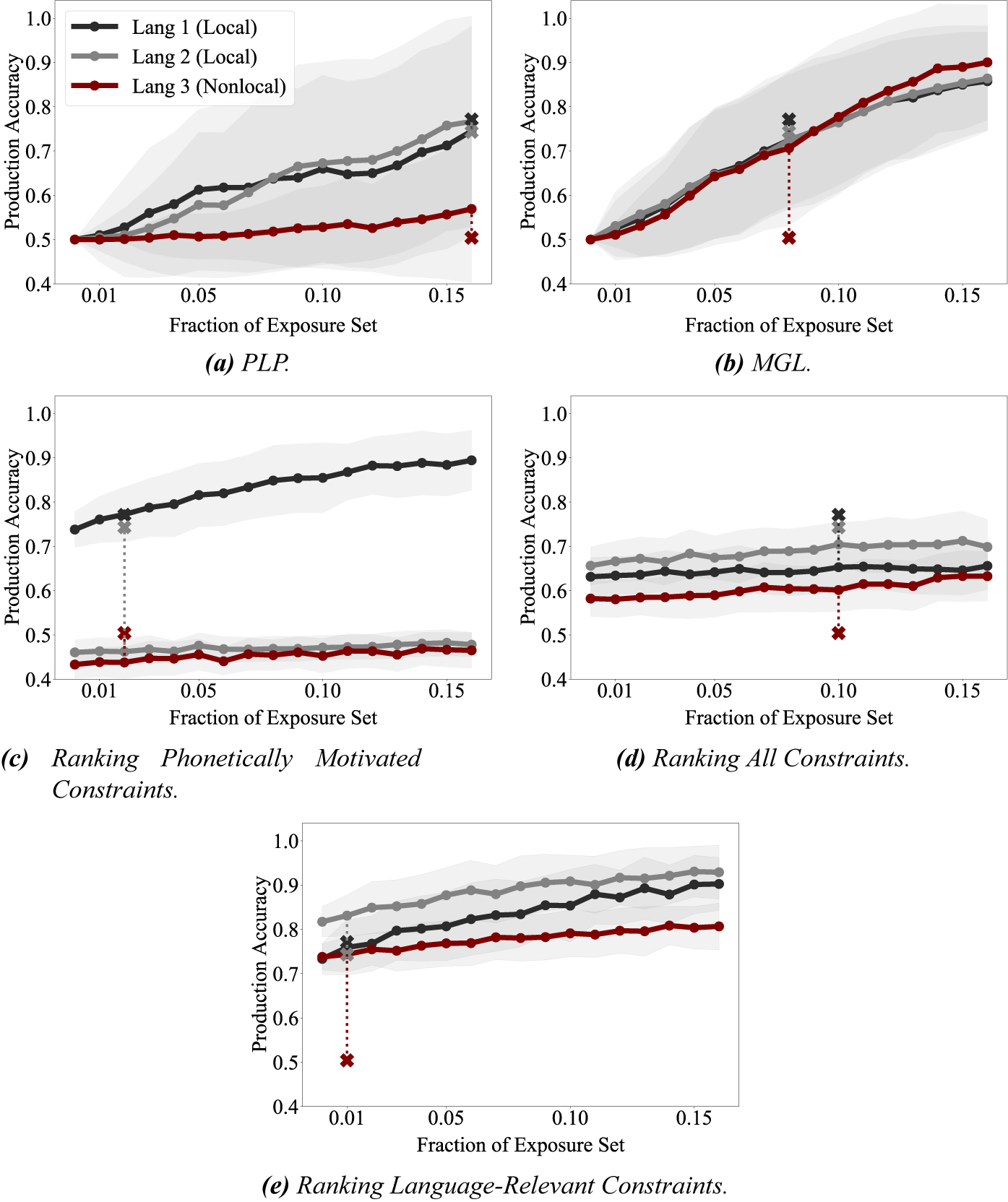
Figure 2 Plots show model accuracies on test words when trained on each of the artificial languages from Baer-Henney & van de Vijver (2012), as a function of the fraction of the exposure set they are trained on. The $\times $ marks show human generalisation accuracy, at the x-axis point where each model best matches human generalisation behaviour. PLP and MGL’s results are in (a) and (b), while grammars learned by ranking a provided constraint set are in (c)–(e). In (c), the ranked constraints are all phonetically motivated; in (d), all constraints needed for the three languages are included and in (e), each model for each language ranks only the constraints relevant to that language.

PLP (Figure 2a) is the best match to the human results, learning the more local generalisations (37a) and (37b) substantially more easily than the less local (37c). This is because PLP requires sufficient evidence against local generalisations (per the Tolerance Principle) before it will abandon them for less local ones (§2.2.2). This is reminiscent of Gómez & Maye’s 2005: 199 characterisation of human learners as attending to local contexts even ‘past the point that such structure is useful’ before eventually moving on to less local information. In contrast, MGL (Figure 2b) learns all three generalisations equally well because it constructs the most conservative – and hence widest-context – generalisation that is sustainable. If a grammar is constructed by ranking a universal constraint set that includes only phonetically motivated constraints (Figure 2c), only the generalisation in (37a) can be learned because that is the only phonetically motivated generalisation. On the other hand, if all relevant constraints are included together (Figure 2d) or on their own (Figure 2e), all three generalisations are learned roughly equally well. This is because learning reduces to constraint ranking – the constraints being provided – and thus fails to distinguish between more and less local constraints. In PLP’s learning of the pattern in (37c), the number of exceptions to the more local generalisation will eventually become too numerous under the Tolerance Principle, and PLP will construct a less local rule, which will correctly characterise the alternation. Thus, PLP predicts that given sufficient time and data, learners will eventually be able to learn the alternation in (37c).

4.2.3. Takeaways

PLP reflects human learners’ preference for local generalisations (Q3).

4.3. Learning German devoicing

I now evaluate PLP on syllable-final obstruent devoicing in German (Wiese 1996).

4.3.1. Setup

This experiment simulates child acquisition by using vocabulary and frequency estimations from child-directed speech in the Leo corpus (Behrens 2006). I retrieved the corpus from the CHILDES database (MacWhinney 2000) and intersected the extracted vocabulary with CELEX (Baayen et al. 1996) to get phonological and orthographic transcriptions for each word. I also computed the frequency of each word in the Leo corpus. The resulting dataset consists of 9,539 words. To construct URs and SRs, I followed Gildea & Jurafsky (1996), using the CELEX phonological representations as SRs and discrepancies between CELEX phonology and orthography to construct URs, since German orthography does not reflect devoicing. Specifically, I make the syllable-final obstruents voiced for the URs of all words where the corresponding orthography indicates a voiced obstruent. In this set of data, only 8.2\% of words involve devoicing, which means a substantial number of SRs are unchanged by this process from the corresponding URs. However, this is an appropriate and realistic scenario, since the data were constructed from child-directed speech, and is thus a reasonable approximation of the data that children have access to when learning this generalisation.

The experimental procedure samples one word at a time from the data, weighted by frequency. The word is presented to each model and added to its vocabulary. Sampling is with replacement, so the learners are expected to encounter the same word multiple times, at frequencies approximating what a child would encounter. When the vocabulary reaches a size of 100, 200, 300 and 400, each model is probed to produce an SR for each UR in the dataset that is not in the vocabulary (i.e., held-out test data). The fraction of these predictions that it gets correct is reported as the model’s accuracy. The models MGL, ED and OSTIA are designed as batch learners, so they are trained from scratch on the vocabulary before each evaluation period. ¹⁴ PLP, Ucon and Oracle learn incrementally.

This simulation is carried out 10 times to simulate multiple learning trajectories. The results are averages and standard deviations over these 10 runs.

Oracle is provided with the constraints in (40).

• 

The markedness constraint *[ $+$ voi, $-$ son] $]_{\sigma }$ , which marks syllable-final voiced obstruents, is the relevant markedness constraint for this process. Ucon is supplied with two additional constraints: *NC̥, which marks voiceless consonants following nasals, and *Complex. Both are frequently considered to be universal, violable constraints (Locke 1983; Rosenthall 1989; Prince & Smolensky 1993; Pater 1999). I included these to capture the assumption of a universal constraint set, which requires learning that *Complex and *NC̥ are violable in German; for instance, // $\rightarrow $ [] (‘believing’) violates *Complex and *NC̥.

4.3.2. Results

The results are shown in Table 1. PLP learns an accurate grammar, which consists of the single generalisaton shown in (41).

• 

Table 1 Model accuracies (with standard deviations) on held-out test data at different training vocabulary sizes. PLP readily learns an accurate generalisation for German syllable-final obstruent devoicing

While PLP achieves perfect accuracy by the time the vocabulary has grown to size 100, it does produce errors in the process of getting there. A primary example is underextensions. In my experiments, underlyingly voiced stops tended to enter the vocabulary earlier than voiced fricatives. Consequently, PLP sometimes fails to extend devoicing to fricatives until evidence of them devoicing enters the vocabulary. These underextensions are over held-out test words – that is, words not in the learner’s vocabulary. Thus, this is a prediction about an early state of the learner’s phonological grammar, and not a prediction that children go through a stage of voicing final voiced fricatves. Indeed, I found that as soon as an instance of fricative devoicing enters the vocabulary, PLP extends the generalisation to account for it.

Ranking a provided constraint set (Oracle and Ucon) can yield the same generalisation as PLP: the sequence [ $+$ voi, $-$ son] $]_{\sigma }$ is not allowed in German, and violations of this restriction are repaired by devoicing. But the differences in how PLP learns this generalisation are informative. Both Ucon and Oracle are provided with the knowledge that the sequence [ $+$ voi, $-$ son] $]_{\sigma }$ is marked. In contrast, PLP discovers the marked sequence in the process of learning.

In German, the onset [] is allowed (e.g., /blɑu/ $\rightarrow $ [blɑu]). PLP always produces the correct SR for /blɑu/ as a consequence of its identity default (Table 2). Whether a constraint-ranking model incorporates a preference for identity between inputs and outputs depends on what constraints it ranks. Because Oracle ranks only the constraints active in the language being learned, it – like PLP– does not produce unmotivated errors. If a universal constraint set is ranked (Ucon), then markedness constraints that are violable in the language being learned will lead to unmotivated errors. For instance, prior to downranking *Complex, Ucon sometimes produces [bәlɑu] for /blɑu/, with the sequence /bl/ broken up by an epenthetic schwa, even though complex onsets are allowed in German. However, deletion tends to be more common than epenthesis as a repair in child utterances, and it appears to be due to articulatory limitations rather than to the child’s hypothesised adult grammar.

Table 2 Analysis of the types of errors each of the models that learn an accurate grammar makes in the process. Because it adds generalisations to the grammar only when necessitated by surface alternations, PLP produces no unmotivated errors

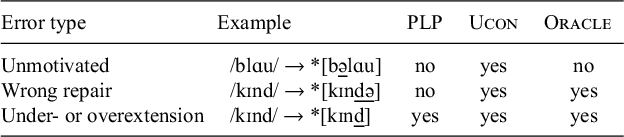
Both Ucon and Oracle sometimes produce // as *[] or *[] rather than [], because they must figure out the relative ranking of faithfulness constraints in order to capture which repair German uses to avoid violations of *[ $+$ voi, $-$ son] $]_{\sigma }$ . In contrast, PLP infers the repair – devoicing – directly from the discrepancy it observes in the data.

None of the other models perform competitively: PLP outperforms them all by a statistically significant amount ( $p < 0.01$ ), as measured by a paired t-test against the null hypothesis that each model’s performance over the 10 simulations has the same average accuracy as PLP’s. MGL, which generalises as conservatively as possible, struggles to generalise beyond the training data. This is seen in its slow rate of improvement. ED is a powerful model in natural language processing when substantial amounts of data are available, but it struggles to learn on the small vocabularies at the scale children learn from. OSTIA struggles even more, consistent with the negative results of Gildea & Jurafsky (1996), who presented it with much larger vocabularies.

4.3.3. Takeaways

PLP is readily able to learn German syllable-final devoicing (Q2) and never introduces unmotivated generalisations (Q3).

4.3.4. Opacity

The associate editor observed that devoicing in Polish interacts opaquely with o-raising, in which // surfaces as [] before word-final oral consonants that are underlyingly voiced (Kenstowicz 1994; Sanders 2003). As a proof of concept, I ran PLP on the data in Sanders (2003: 48–51). PLP learned the counterbleeding rule system in (42), with raising ( $r_1$ ) correctly ordered before devoicing ( $r_2$ ). ¹⁵

• 

Rule $r_2$ accounts for devoicing both in isolation (43a) and in words exhibiting raising (43c). Rule $r_1$ accounts for raising both in isolation (43b) and when its underlying context is opaquely obscured by devoicing (43c).

• 

The correct ordering was achieved because the reverse ordering, in which devoicing bleeds raising, results in errors like *[] for //. This demonstrates that PLP is capable of handling at least this case of opacity. I leave a systematic study of opacity for future work (see §2.3.3).

4.4. Learning a multi-process grammar

This experiment evaluates PLP at learning multiple generalisations simultaneously. The processes modelled are the English alternating plural and 3sg.pres affix /-/ (44a), the alternating past tense affix /-/ (44b), and vowel nasalisation (44c).

• 

4.4.1. Setup

This experiment, like the first, simulates child language acquisition. The child-directed speech is aggregated across English corpora in CHILDES (MacWhinney 2000), including the frequency of each word. Only words with ‘\%mor’ tags were retained, because the morphological information was needed to construct URs. Transcriptions from the CMU Pronouncing Dictionary (Weide 2014) served as SRs, with nasalisation added to vowels preceding nasal consonants. URs had all vowels recorded without nasalisation. The URs of the affixes on all past tense verbs, plural nouns and 3sg.pres verbs were set to /d/, /z/ and /z/, respectively. The resulting dataset contains 20,421 UR–SR pairs.

The experimental procedure is the same as for German, sampling words weighted by frequency and reporting accuracies at predicting SRs from URs over held-out test words when each learner’s vocabulary reaches certain sizes: 1K, 2K, 3K and 4K words.

I omit results from MGL, ED and OSTIA because they continued to be non-competitive. Oracle once again ranks only the relevant constraints, listed in (45), and Ucon receives these plus *Complex and *NC̥.

• 

All faithfulness constraints other than Dep were split into two – one for stems and one for affixes – so that, for instance, *[] could be ruled out for input // in (44a).

4.4.2. Results

The models’ accuracies on held-out test words, shown in Table 3, reveal that PLP learns an accurate grammar by the time its vocabulary grows to about 2,000 words. PLP’s output is shown as an ordered list of rules in (46).

Table 3 Model accuracies (with standard deviations) on held-out test data at different training vocabulary sizes. PLP readily learns an accurate grammar for the English processes in (44)

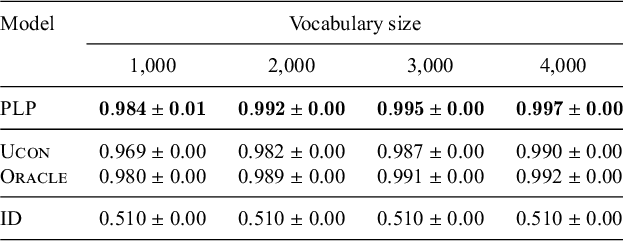
Figure 3 PLP’s accuracy on the plural and past tense nonce words from Berko (1958) as training progressed. The black dashed line denotes plurals that should take [-z] or [-s] and the grey dashed lines those that should take [-әz]. The dotted lines represent the analogues for past tense. The fact that [-z]/[-s] accuracy converges before [-әz] and [-d]/[-t] before [-әd] matches Berko’s finding that children learn [-z]/[-s] and [-d]/[-t] before [-әz] and [-әd].

• 

The rules were ordered as described in §2.3.3, with $r_2$ before $r_3$ and $r_4$ before $r_5$ (bleeding order) being the inferred ordering dependencies. Thus, as described in §2.3.3, PLP learned that epenthesis bleeds devoicing. Rules $r_2$ – $r_5$ do not encode a word-final context because they satisfy the Tolerance Principle threshold without it, so there is no need for PLP to expand the search window. The extension of [ $+$ cor, $-$ cont, $-$ nas] is {}, and the extension of [ $+$ cor, $-$ cont, $-$ nas, $+$ voi] is {}.

The fact that no model achieves 100\% accuracy is due to a handful of words that do not follow the generalisations in (44). For instance, compounds like [] allow the sequence [], but the models predict there should be an epenthetic vowel to split the sequence. Such exceptions are easily accounted for if I assume the learner recognises the word as a compound. Since exceptions are inevitable in naturalistic data, I chose to not remove them.

Berko’s (1958) seminal study found that children aged 4–7 years could accurately inflect nonce words that take the [-z], [-s], [-d] or [-t] suffixes, but that they performed much worse at inflecting nonce words taking the [-әz] or [-әd] suffixes. Adults could inflect nonce words with [-әz] or [-әd], suggesting that voicing assimilation process may be learned earlier than the epenthesis process. I show PLP’s accuracy on Berko’s different categories of nonce words in Figure 3 as the vocabulary grows (x-axis). PLP’s accuracy on nonce words taking [-z] or [-s] (dashed black line) converges earlier than its accuracy on nonce words taking [-әz] (dashed grey line); similarly the accuracy for nonce words taking [-d] or [-t] (dotted black line) converges earlier than for nonce words taking [-әd] (dotted grey line). Thus, the order of acquisition matches Berko’s finding.

4.4.3. Takeaways

The results in this more challenging setting, where multiple processes are simultaneously active, support the takeaways from the prior experiment. PLP successfully learns all the generalisations (Q2) and does not introduce unmotivated generalisations (Q3).

4.5. Learning Tswana’s post-nasal devoicing

Although a majority of phonological patterns may be phonetically grounded, some processes nevertheless appear to lack or even oppose phonetic motivation (Anderson 1981; Buckley 2000; Johnsen 2012; Beguš 2019). Moreover, these must still be learnable, because children continue to successfully acquire them (Johnsen 2012: 506). An example of such a pattern is the post-nasal devoicing in Tswana shown above in (2), which Coetzee & Pretorius (2010) confirmed to be productive despite operating against the phonetic motivation for post-nasal voicing (Hayes & Stivers 2000; Beguš 2019). Beguš (2019: 699) found post-nasal devoicing reported as a sound change in 13 languages and dialects, from eight language families.

Models of phonological learning should account for the fact that productive patterns are successfully learned by humans even if they are not phonetically grounded. A consequence of PLP’s identity default is that generalisations are added to the grammar whenever they are motivated by surface alternations. Since surface alternations in Tswana motivate a generalisation for post-nasal devoicing, PLP should be able to acquire the Tswana pattern. This experiment attempts to confirm this (Q3).

4.5.1. Setup

For this experiment, I used the 10 UR–SR pairs from Coetzee & Pretorius (2010: 406) as training data. Five pairs involve devoicing resulting from the 1sg.obj clitic /m/ attaching to a stem that starts with a voiced obstruent. The other five pairs involve the 1pl.obj clitic /re/ attaching to the same stems, which serve as negative examples since the clitic does not introduce a nasal. These data are not necessarily representative of the data a child would have during acquisition, and the learnability experiment thus serves only as a proof of concept.

Table 4 PLP learns precisely the set of processes active in its experience. This provides a straightforward account of how productive phonological processes can be learned even if they operate against apparent phonetic motivation, like devoicing in Tswana following nasals (Coetzee & Pretorius 2010). With PLP, the unmotivated constraint *NC̬ need not be assumed to be universal

The test data consist of the same 20 /b/-initial nonce words presented to the participants in Coetzee & Pretorius (2010: 407) – 10 stems each combined with /m/ and /re/.

4.5.2. Results

The results in Table 4 demonstrate that PLP can learn Tswana’s post-nasal devoicing without requiring the existence of a phonetically unmotivated universal constraint. ¹⁷ Constraint-ranking models can also learn the generalisation but depend on an account of how the constraint *NC̬, which penalises what is not usually considered to be a universally marked sequence (Locke 1983; Rosenthall 1989; Pater 1999; Beguš 2016, 2019), is added to the constraint set.

4.5.3. Takeaways

Because PLP assumes UR–SR identity by default, it constructs precisely the generalisations necessary to account for the discrepancies active in its experience, providing a straightforward account of how productive generalisations can be learned even if they are opposed to apparent phonetic motivation, as humans evidently do (Q3; see Seidl & Buckley 2005, Johnsen 2012: 506; Beguš 2018, ch. 6).

5. Discussion

5.1. The nature of locality

One reviewer asked what sort of tendency I view locality to be. I view the cognitive tendency for humans to prefer constructing local generalisations to be a geometric computational consequence. That is, if words are viewed, at least to a first approximation, as linear objects, this linear geometry introduces the notion of locality as small linear distance. In my view, the reason that a human is more likely to construct a generalisation that conditions $x_i$ on $x_{i-1}$ than on $x_{i-2}$ in a sequence $\ldots , x_{i-2}, x_{i-1}, x_i$ (see §1.1) is that a search outward from $x_i$ encounters $x_{i-1}$ before it encounters $x_{i-2}$ .

PLP is an attempt to state this in explicit computational terms. An immediate consequence of this hypothesis is that if $x_{i-1}$ is sufficient to account for whatever the uncertainty in $x_i$ is (e.g., what its surface form is), then $x_{i-2}$ will never be considered, even if there is some statistical dependency between the two. I believe this prediction is consistent with the experimental results from sequence learning, discussed in §1.1, in which participants tracked adjacent dependencies even when non-adjacent dependencies were more statistically informative (Gómez & Maye 2005) and constructed local generalisations rather than less local ones when the exposure data underdetermined the two (as in the poverty-of-stimulus paradigms of Finley 2011 and McMullin & Hansson 2019). I note that words may not be exactly linear – segment articulations have gestural overlap, syllables are often viewed as hierarchical structures, and representations like autosegmental tiers may be present. However, I think treating words as linear sequences is a good first approximation. Work on tier-locality also recognises that string-locality is a special case of tier-locality in which all segments are on the same tier (see, e.g., Hayes & Wilson 2008; Heinz et al. 2011; McMullin 2016).

An alternative view could be that locality is distributional: a learner may track the dependency between $x_i$ and both $x_{i-1}$ and $x_{i-2}$ , and may find that $x_{i-1}$ is more statistically robust as a generalisation, preferring it for that reason. However, this view is inconsistent with the findings that when statistical robustness is controlled (Finley 2011; McMullin & Hansson 2019), and even when it favours the less local dependency (Gómez & Maye 2005), humans systematically generalise locally. The distributional approach could be combined with a stipulated bias (prior) favouring local dependencies, but this would simply describe the phenomenon, not explain it.

5.2. Future directions

Research on phonological representations recognises that strict locality arises not only over string representations but also over representations like tiers and metrical grids (Goldsmith 1976; Hayes & Wilson 2008; Heinz et al. 2011; McMullin 2016). PLP could be extended to construct generalisations over these representations. However, an account of how a learner may construct increasingly abstract representations should first be given. Recent work has investigated this, proposing an abductive algorithm in which learners iteratively propose new representations in response to alternations not being sufficiently predictable from adjacent dependencies in a linear representation (Belth in press). This mirrors PLP’s iterative expansion of an attention window. Future work will investigate combining these learning models: it remains an open question how the mechanisms of expanding attention and projecting new representations interact.

In another direction, variation is an important aspect of phonology (Coetzee & Pater 2011). PLP currently learns categorical processes, and future work will investigate extending PLP to handle variation by allowing rules to be probabilistic.