Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T14:52:45.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Ecological Regression with Partial Identification

Published online by Cambridge University Press:  02 August 2019

Wenxin Jiang ,
Gary King Open the ORCID record for Gary King [Opens in a new window] ,
Allen Schmaltz Open the ORCID record for Allen Schmaltz [Opens in a new window]  and
Martin A. Tanner
Wenxin Jiang
Affiliation:
Institute of Finance (Adjunct), Shandong University, Jinan, Shandong, China. Email: wjiang@northwestern.edu Department of Statistics, Northwestern University, Evanston, IL, USA. Email: mat132@northwestern.edu
Gary King
Affiliation:
Institute for Quantitative Social Science, Harvard University, Cambridge, MA, USA. Email: king@harvard.edu, schmaltz@fas.harvard.edu
Allen Schmaltz*
Affiliation:
Institute for Quantitative Social Science, Harvard University, Cambridge, MA, USA. Email: king@harvard.edu, schmaltz@fas.harvard.edu
Martin A. Tanner
Affiliation:
Department of Statistics, Northwestern University, Evanston, IL, USA. Email: mat132@northwestern.edu
*
*Email: schmaltz@fas.harvard.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Ecological inference (EI) is the process of learning about individual behavior from aggregate data. We relax assumptions by allowing for “linear contextual effects,” which previous works have regarded as plausible but avoided due to nonidentification, a problem we sidestep by deriving bounds instead of point estimates. In this way, we offer a conceptual framework to improve on the Duncan–Davis bound, derived more than 65 years ago. To study the effectiveness of our approach, we collect and analyze 8,430 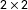$2\times 2$ EI datasets with known ground truth from several sources—thus bringing considerably more data to bear on the problem than the existing dozen or so datasets available in the literature for evaluating EI estimators. For the 88% of real data sets in our collection that fit a proposed rule, our approach reduces the width of the Duncan–Davis bound, on average, by about 44%, while still capturing the true district-level parameter about 99% of the time. The remaining 12% revert to the Duncan–Davis bound.

Keywords

asymptoticsboundsconfidence intervalscontextual modelsecological inferencelinear regressionpartial identification
Type
Articles
Information
Political Analysis , Volume 28 , Issue 1 , January 2020 , pp. 65 - 86
Copyright
Copyright © The Author(s) 2019. Published by Cambridge University Press on behalf of the Society for Political Methodology. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Authors’ note: We thank the editor and anonymous reviewers for their helpful comments. This work was partially supported by the Taishan Scholar Construction Project to W.J. and by the Institute for Quantitative Social Science.

Contributing Editor: Jeff Gill

References

Achen, C. H., and Shively, W. P.. 1995. Cross-Level Inference . Chicago: University of Chicago Press.Google Scholar
Altman, M., Gill, J., and McDonald, M.. 2004. A Comparison of the Numerical Properties of EI Methods , edited by King, G., Rosen, O., and Tanner, M. A., 383–409. New York: Cambridge University Press.Google Scholar
Centers for Disease Control and Prevention (CDC), National Center for Health Statistics. 2017. Underlying Cause of Death 1999–2016 on CDC WONDER Online Database. Data are from the Multiple Cause of Death Files, 1999–2016, as compiled from data provided by the 57 vital statistics jurisdictions through the Vital Statistics Cooperative Program. Accessed at http://wonder.cdc.gov/ucd-icd10.html(retrieved in 2017).Google Scholar
Chambers, R. L., and Steel, D. G.. 2001. “Simple Methods for Ecological Inference in $2\times 2$ Tables.” Journal of Royal Statistical Society Series A 164(Part 1):175–192.Google Scholar
Chernozhukov, V., Hong, H., and Tamer, E.. 2007. “Estimation and Confidence Regions for Parameter Sets in Econometric Models.” Econometrica 75:1243–1284.Google Scholar
Cho, W. K. T., and Manski, C. F.. 2008. “Cross Level/Ecological Inference.” In Oxford Handbook of Political Methodology , edited by Box-Steffensmeier, J., Brady, H., and Collier, D., 530–569. Oxford, UK: Oxford University Press.Google Scholar
Duncan, O. D., and Davis, B.. 1953. “An Alternative to Ecological Correlation.” American Sociological Review 18:665–666.Google Scholar
Freedman, D. A., Klein, S. P., Sacks, J., Smyth, C. A., and Everett, C. G.. 1991. “Ecological Regression and Voting Rights.” Evaluation Review 15:659–817 (with discussion).Google Scholar
Goodman, L. 1953. “Ecological Regression and the Behavior of Individuals.” American Sociological Review 18:663–664.Google Scholar
Imai, K., Lu, Y., and Strauss, A.. 2008. “Bayesian and Likelihood Inference for $2\times 2$ Ecological Tables: An Incomplete Data Approach.” Political Analysis 16(1):41–69.Google Scholar
Jiang, W., King, G., Schmaltz, A., and Tanner, M. A.. 2019. “Replication Data for: Ecological Regression with Partial Identification,” https://doi.org/10.7910/DVN/W7KZVL, Harvard Dataverse, V1.Google Scholar
Jiang, W., King, G., Schmaltz, A., and Tanner, M. A.. 2018. Ecological Regression with Partial Identification. Technical Report. https://arxiv.org/abs/1804.05803. Replication Data: https://doi.org/10.7910/DVN/8TB7GO, Harvard Dataverse, V1.Google Scholar
King, G. 1997. A Solution to the Ecological Inference Problem: Reconstructing Individual Behavior from Aggregate Data . Princeton: Princeton University Press.Google Scholar
King, G., Rosen, O., and Tanner, M. A.. 2004. Ecological Inference: New Methodological Strategies . New York: Cambridge University Press.Google Scholar
Liao, Y., and Jiang, W.. 2010. “Bayesian Analysis in Moment Inequality Models.” The Annals of Statistics 38:275–316.Google Scholar
Office of the Registrar General & Census Commissioner, India. 2001. Census of India 2001. Accessed at https://data.gov.in(retrieved in 2017).Google Scholar
Owen, G., and Grofman, B.. 1997. “Estimating the Likelihood of Fallacious Ecological Inference: Linear Ecological Regression in the Presence Context Effects.” Political Geography 16:675–690.Google Scholar
Ruggles, S., Genadek, K., Goeken, R., Grover, J., and Sobek, M.. 2017. Integrated Public Use Microdata Series: Version 7.0 [dataset] . Minneapolis, MN: University of Minnesota, 2017. https://doi.org/10.18128/D010.V7.0. Accessed at https://usa.ipums.org/usa/ (retrieved in 2018).Google Scholar
Wakefield, J. 2004. “Prior and Likelihood Choices in the Analysis of Ecological Data.” In Ecological Inference: New Methodological Strategies , edited by King, G., Rosen, O., and Tanner, M. A., 13–50. New York: Cambridge University Press.Google Scholar
Supplementary material: File

Jiang et al. supplementary material

Jiang et al. supplementary material 1

Download Jiang et al. supplementary material(File)
File 198.1 KB