1. Introduction
Survey experiments are increasingly used in the social sciences and other fields in large part because they provide strong internal validity, allowing researchers to evaluate the causal impact of an intervention among respondents. In these studies, researchers are typically interested in learning about the impact of a given treatment not just in the observed sample, but in some broader population. Survey experiments conducted on representative probability samples are therefore often viewed as the “gold standard” for answering questions about population-level causal effects (Druckman and Green Reference Druckman and Green2021; Mutz Reference Mutz2011).
A key assumption that allows for generalization of sample treatment effect estimates to a broader population is that the sample is representative of the population on important treatment effect moderators, perhaps conditional on some observed covariates (Egami and Hartman Reference Egami and Hartman2021). But with response rates in modern surveys often falling below 10% (Kennedy and Hartig Reference Kennedy and Hartig2019), even high-quality surveys could suffer from significant nonresponse bias if the people who tend to participate in the survey are systematically different from those who typically refuse to participate (Dutwin et al. Reference Dutwin2014). And, with recent calls in behavioral science for a “heterogeneity revolution” that tests theories on nonstandard participants, it is important to examine the generalizability of experimental findings to atypical respondents (Bryan, Tipton, and Yeager Reference Bryan, Tipton and Yeager2021).
Are treatment effects in survey experiments similar for people who are reluctant versus eager to respond? Or is this at least true conditional on commonly used covariates such as demographics? If an experiment’s treatment effects differ between the people likely to respond to a survey and those who are reluctant to respond, then effects estimated from the survey sample may not generalize to the broader population. This could happen, for example, if people eager to respond to surveys are also more engaged with the experimental stimuli (Eagly and Chaiken Reference Eagly and Chaiken1993; Malhotra, Miller, and Wedeking Reference Malhotra, Miller and Wedeking2014; Petty and Cacioppo Reference Petty, Cacioppo and Berkowitz1986). These concerns underlie fundamental questions about the generalizability of experimental findings (e.g., Egami and Hartman Reference Egami and Hartman2023; Findley, Kikuta, and Denly Reference Findley, Kikuta and Denly2021; Stuart et al. Reference Stuart, Cole, Bradshaw and Leaf2011; Tipton Reference Tipton2014). Generalizability is a subset of the concerns underlying external validity of experiments, which considers changes to the units, treatments, outcomes, or context of an experiment (Cook, Campbell, and Shadish Reference Cook, Campbell and Shadish2002; Egami and Hartman Reference Egami and Hartman2023). We emphasize that we focus here on the generalizability of experimental units to a broader, or different, population. Other dimensions of external validity of survey experiments, such as for treatments and outcomes, are a separate and open question (e.g., Brutger et al. Reference Brutger, Kertzer, Renshon and Weiss2022), and one which we believe is a core part of critics’ concerns about survey experiments.
Previous work suggests that treatment effect estimates from survey experiments are similar whether based on probability samples or on less expensive online convenience samples, likely due to a lack of substantial treatment effect heterogeneity (Berinsky, Huber, and Lenz Reference Berinsky, Huber and Lenz2012; Coppock, Leeper, and Mullinix Reference Coppock, Leeper and Mullinix2018; Coppock and McClellan Reference Coppock and McClellan2019; Miratrix et al. Reference Miratrix, Sekhon, Theodoridis and Campos2018). But these findings compare estimates from probability samples that already over-represent eager respondents with estimates from convenience samples that overrepresent eager respondents even more. Thus, it may be little reassurance that one can obtain similar (perhaps similarly biased) estimates from probability samples with severe nonresponse as from cheaper convenience samples. Other efforts to generalize estimates from survey data focus on weighting, or adjusting, surveys that are unrepresentative using observable demographic characteristics (Franco et al. Reference Franco, Malhotra, Simonovits and Zigerell2017; Miratrix et al. Reference Miratrix, Sekhon, Theodoridis and Campos2018). But when even high-quality public opinion surveys produce single digit response percentages, a key concern is whether the small fraction of population members who are eager to respond to surveys are similar in relevant respects, particularly on treatment effect moderators, to those who are more reluctant, or refuse, to participate in them.
We show in Section 3 that bias from attempting to generalize unrepresentative samples to broader populations can arise when treatment effects are heterogeneous, some population members are more eager to respond to these surveys (and thus are overrepresented in the sample), and this response eagerness is correlated with the individual-level treatment effects. Unlike many demographic variables which may be suspected to moderate treatment effects, response reluctance is typically not known for respondents and therefore cannot be directly adjusted for using weighting or other methods within a given sample. Evaluating this concern about generalizing toward populations that consist overwhelmingly of reluctant respondents requires data that include a large number of both eager and reluctant respondents as well as a way of differentiating these two groups within the survey. Moreover, since the nature of treatment effects is specific to the experiment in question and therefore treatment effects in some studies may be more related to response eagerness than in others, an evaluation of generalizability would ideally include data across a broad set of survey experiments covering the sorts of topics that are studied in the social sciences.
The article proceeds as follows. First, we introduce the collection of experimental studies we analyze and we describe the unique features about the recruitment method that make these data so well-suited for our purposes. Next, we provide an intuition for the types of respondents included in different approaches to respondent recruitment and we formally characterize the conditions under which the overrepresentation of eager survey respondents can create bias in treatment effect estimates. We then compare treatment effect estimates among eager and reluctant respondents, including within various demographic subgroups, and we formally evaluate treatment effect heterogeneity using causal random forests. Finally, we estimate the probability of being a reluctant respondent using random forests in order to estimate the correlation between treatment effect heterogeneity and reluctance, as well as assess the plausibility that hypothetical unobserved confounders exist with the properties necessary to meaningfully bias estimates. Our findings suggest that across a wide range of survey experiments, average treatment effects are similar between eager and reluctant respondents.
2. Empirical Analysis: Time-Sharing Experiments in the Social Sciences Experiments
To assess the generalizability of survey experiments, we focus on a large set of survey experiments that cover a wide range of social science topics. Specifically, we obtained data from 50 studies fielded by the Time-Sharing Experiments in the Social Sciences (TESS) program, which is supported by the National Science Foundation, from May 2017 to April 2020. This includes the universe of all unembargoed studies conducted by NORC that were available when we obtained these data, and represents a broad cross section of typical survey experiments conducted in the social sciences. Faculty members, postdocs, and graduate students anywhere in the world are eligible to apply to conduct a study through TESS. To do so, they must submit a description of their study and the design for a survey experiment, which then undergoes double-blind peer review. Accepted TESS survey experimental proposals are fielded free of charge by the nonpartisan and objective research organization NORC at the University of Chicago, typically to a nationally representative probability sample of American adults, but sometimes to more specific samples. Supplementary Table D2 lists these studies, including titles, authors, sample size, and sampling frame. The competitive nature of the TESS proposal process means that the set of studies we analyze reflect high-quality survey experiments with designs that social scientists believe are important and promising. These studies, then, are the type for which generalizability is important to evaluate.
The studies we analyze are fielded on NORC’s AmeriSpeak Panel, which is recruited through a two-step process that provides unique advantages for answering our questions of interest (NORC 2021). First, potential panelists, drawn using a probability sample from an address-based sampling frame, are invited to participate using a basic initial contact. This first contact is relatively low-intensity, consisting of mailings, phone calls, and modest offers of incentives. These are fairly standard recruitment strategies for many national probability samples. Then, among those who do not initially agree to participate, a random subset of people is selected for much more intensive “nonresponse follow-up” (NRFU) recruitment which involves multiple contacts, offers of enhanced compensation, and even face-to-face recruitment (door knocks) by professional field interviewers. The incentives offered during the NRFU recruitment were significantly larger than those offered during the initial recruitment stage. Initial recruitment typically includes $5 initially (some earlier panelists were offered only $2) and $20 upon joining the panel, while NRFU recruitment includes $10 in a mailer with $50 more promised upon joining the panel (see Supplementary Section B for more information). Moreover, 84% of those recruited through NRFU received in person contacts (door knocks) prior to their joining, with the remainder joining before the in person contact was attempted, typically very shortly after receiving the mailer with offers of enhanced compensation. We obtained previously unavailable information about the recruitment method for each individual respondent in each of these 50 TESS studies, specifically whether an individual required an NRFU or whether they agreed to participate after the initial low-intensity recruitment.
The recruitment rate for initial contact is around 6%, while the recruitment rate for respondents selected for NRFU is nearly five times as high at around 28%, raising the overall weighted panel household AAPOR RR3 response rate by a factor of about 5 (see Bilgen, Dennis, and Ganesh Reference Bilgen, Dennis and Ganesh2018 for more information). NORC recruits new panelists, including with NRFU recruitment, every year (except during the COVID-19 pandemic) to grow the panel and address attrition. The median tenure for eager recruits, as of 2023, is 4.3 years, and for reluctant respondents it is 4.7 years. This additional effort to reach reluctant respondents has been shown to improve recruitment of groups including younger and less educated respondents as well as Hispanics and also produces respondents who tend to be more politically moderate and somewhat more conservative on average (Bilgen, Dennis, and Ganesh Reference Bilgen, Dennis and Ganesh2018, Reference Bilgen, Dennis and Ganesh2019). We confirm many of these findings in Section 4.3, where we find that income, religious attendance, party ID, and age are all predictive of response reluctance. Our approach also shares some similarities with Brehm (Reference Brehm1993) who applies methods proposed by Heckman (Reference Heckman1979) and Achen (Reference Achen1986) to adjust for nonresponse in regression models using data from the American National Election Studies and other sources. Finally, we note that across studies, the average response rate for panelists recruited to a given survey is 34%.
The demographic characteristics of respondents in our studies’ samples who are recruited via initial contacts and those recruited through NRFU are fairly similar overall (see Supplementary Section A for more information). The average percentage of respondents recruited via NRFU in our studies is 37.96% (SD
![]() $=$
7.2). The average weighted by sample size is very similar at 38.05%, which is similar to the overall AmeriSpeak 2014–2019 panelists, where 38% were recruited via NRFU.
$=$
7.2). The average weighted by sample size is very similar at 38.05%, which is similar to the overall AmeriSpeak 2014–2019 panelists, where 38% were recruited via NRFU.
NRFU respondents contain slightly more Independents (16% vs. 15%) and are somewhat more likely to have lower levels of educational attainment (in particular 33% of NRFU respondents have a BA or higher, as compared to 40% of eager recruits) and include a lower proportion of whites (60% vs. 68%).
3. Understanding the Potential for Bias
One can imagine a spectrum ranging from respondents who are very eager to respond to surveys to those who are very reluctant to do so. The first group would typically participate in a wide range of surveys, including low-cost convenience sample surveys as well as high-quality probability-sample surveys, appearing with disproportionate frequency in these samples; the latter would rarely, if ever, be included in survey samples. In survey experiments (and surveys more generally), many approaches exist to generating samples of respondents. Broadly, sampling schemes can be classified as either probability or nonprobability, with both subject to nonrandom nonresponse. Nonprobability sampling schemes include maintained panels, which can be recruited or opt-in and can be combined with a secondary probability sampling or quota design, and river sampling designs, which use similar recruitment practices for one-off surveys (Mercer et al. Reference Mercer, Kreuter, Keeter and Stuart2017). Different sampling schemes are more or less likely to include different types of respondents, with convenience-based river surveys more likely to over-represent eager respondents, and probability-based samples with intense recruitment, such as NORC’s NRFU, more likely to include reluctant respondents. No design can guarantee that the most reluctant individuals respond, but our goal is to show that survey experiments among more eager respondents generalize well to a pool of more reluctant respondents. Figure 1 provides an informal illustration of the spectrum of eagerness versus reluctance and different types of samples.
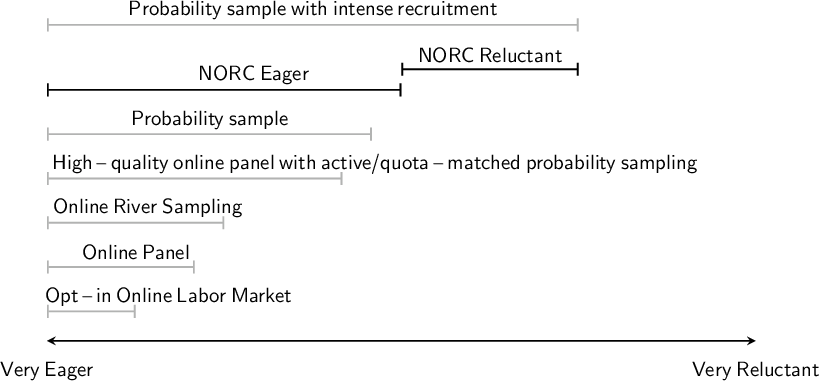
Figure 1 Example ranges of respondent eagerness/reluctance among different types of samples. Ranges chosen for illustrative purposes.
If the quantity of interest—in the case of survey experiments, average treatment effects—is uncorrelated with eagerness to respond to surveys, it would not be problematic to use standard survey samples, even those subject to strong nonresponse bias, to learn about population-level treatment effects. But if eagerness is related to treatment effects, then common estimators may be biased.
To illustrate this formally and following Miratrix et al. (Reference Miratrix, Sekhon, Theodoridis and Campos2018), assume a population of size N, from which an experimental survey sample of size n is realized. Let
![]() $R_i \in \{0, 1\}$
be an indicator for whether unit i is included in the survey sample and
$R_i \in \{0, 1\}$
be an indicator for whether unit i is included in the survey sample and
![]() $\mathcal {R}$
denote the set of units with
$\mathcal {R}$
denote the set of units with
![]() $R_i = 1$
. The inclusion probability,
$R_i = 1$
. The inclusion probability,
![]() $\pi _i \equiv \Pr (R_i = 1) = \mathbb {E}[R_i]$
, is the probability that unit i is included in the experimental sample. This inclusion probability may be fully unknown, due to convenience sampling, or the product of a known sampling probability and an unknown response probability. For ease of notation, we define
$\pi _i \equiv \Pr (R_i = 1) = \mathbb {E}[R_i]$
, is the probability that unit i is included in the experimental sample. This inclusion probability may be fully unknown, due to convenience sampling, or the product of a known sampling probability and an unknown response probability. For ease of notation, we define
![]() $\pi _i^{*} = \frac {\pi _i}{\bar {\pi }}$
, which is the normalized inclusion probability such that the mean inclusion probability is 1. Estimated survey weights are typically proportional to
$\pi _i^{*} = \frac {\pi _i}{\bar {\pi }}$
, which is the normalized inclusion probability such that the mean inclusion probability is 1. Estimated survey weights are typically proportional to
![]() ${\pi _i^{*}}^{-1}$
. Let the unit-level treatment effect for unit i be
${\pi _i^{*}}^{-1}$
. Let the unit-level treatment effect for unit i be
![]() $\tau _i = Y_i(1) - Y_i(0)$
, where
$\tau _i = Y_i(1) - Y_i(0)$
, where
![]() $Y_i(t)$
is the potential outcome for unit i under treatment status
$Y_i(t)$
is the potential outcome for unit i under treatment status
![]() $t \in \{0, 1\}$
. We assume an individual’s treatment assignment,
$t \in \{0, 1\}$
. We assume an individual’s treatment assignment,
![]() $T_i$
, is randomized, under complete randomization, within the survey experiment. Our quantity of interest is the Population Average Treatment Effect (PATE), which is defined as
$T_i$
, is randomized, under complete randomization, within the survey experiment. Our quantity of interest is the Population Average Treatment Effect (PATE), which is defined as
![]() $\tau = \mathbb {E}[Y_i(1) - Y_i(0)]$
, where the expectation is taken over the distribution of units in the target population.
$\tau = \mathbb {E}[Y_i(1) - Y_i(0)]$
, where the expectation is taken over the distribution of units in the target population.
We define the difference-in-means estimator within the survey experimental sample as
![]() $\hat {\tau }_{dim} = \frac {1}{n_t}\sum _{i : T_i = 1} Y_i - \frac {1}{n_c}\sum _{i : T_i = 0} Y_i$
, where
$\hat {\tau }_{dim} = \frac {1}{n_t}\sum _{i : T_i = 1} Y_i - \frac {1}{n_c}\sum _{i : T_i = 0} Y_i$
, where
![]() $n_t$
and
$n_t$
and
![]() $n_c$
are the number of treated and control units, respectively. The bias of the difference-in-means estimator in the survey sample, over repeated draws from the population and relative to the population level average effect, is
$n_c$
are the number of treated and control units, respectively. The bias of the difference-in-means estimator in the survey sample, over repeated draws from the population and relative to the population level average effect, is
where
![]() $\sigma _{\pi _i^{*}}$
and
$\sigma _{\pi _i^{*}}$
and
![]() $\sigma _{\tau _i}$
are the standard deviation of the normalized inclusion probability and the unit-level treatment effect, respectively, and
$\sigma _{\tau _i}$
are the standard deviation of the normalized inclusion probability and the unit-level treatment effect, respectively, and
![]() $\rho _{\pi _i^{*},\tau _i}$
captures the correlation between the inclusion probability and the treatment effect. The proof can be found in Supplementary Appendix C. The term
$\rho _{\pi _i^{*},\tau _i}$
captures the correlation between the inclusion probability and the treatment effect. The proof can be found in Supplementary Appendix C. The term
![]() $\pi _i^{*}$
captures the relative probability of inclusion, with mean 1, where weights over 1 mean that a unit is overrepresented in the sample, and less than 1 mean that they are of a type that is typically underrepresented. We can think of
$\pi _i^{*}$
captures the relative probability of inclusion, with mean 1, where weights over 1 mean that a unit is overrepresented in the sample, and less than 1 mean that they are of a type that is typically underrepresented. We can think of
![]() $\pi _i^{*}$
as related to eagerness since respondents who are more eager to respond to surveys will tend to be overrepresented in surveys samples relative to their share of the population and therefore will have higher
$\pi _i^{*}$
as related to eagerness since respondents who are more eager to respond to surveys will tend to be overrepresented in surveys samples relative to their share of the population and therefore will have higher
![]() $\pi _i^{*}$
( and we would typically estimate lower weights for them when adjusting for nonresponse) than reluctant respondents. Thus, the difference-in-means estimator of the average treatment effect is biased toward the average treatment effect among these over-represented units.
$\pi _i^{*}$
( and we would typically estimate lower weights for them when adjusting for nonresponse) than reluctant respondents. Thus, the difference-in-means estimator of the average treatment effect is biased toward the average treatment effect among these over-represented units.
What this makes clear is that bias occurs when observations with small or large treatment effects have small or large relative probabilities of inclusion (i.e.,
![]() $\rho _{\pi _i^{*} \tau _i} \ne 0$
). In other words, for bias to occur, there needs to be some correlation between eagerness to respond to the survey and treatment effect heterogeneity. If there is no treatment effect heterogeneity (i.e.,
$\rho _{\pi _i^{*} \tau _i} \ne 0$
). In other words, for bias to occur, there needs to be some correlation between eagerness to respond to the survey and treatment effect heterogeneity. If there is no treatment effect heterogeneity (i.e.,
![]() $\sigma _{\tau _i} = 0$
), then there will be no bias. Similarly, if the sample is representative and hence all the relative inclusion probabilities are 1 (i.e.,
$\sigma _{\tau _i} = 0$
), then there will be no bias. Similarly, if the sample is representative and hence all the relative inclusion probabilities are 1 (i.e.,
![]() $\sigma _{\pi _i^{*}} = 0$
), then there will be no bias. Thus, we are concerned about scenarios where treatment effect heterogeneity exists and is correlated with survey response eagerness. Equation (1) shows that if eagerness to respond to surveys is related to the individual-level treatment
$\sigma _{\pi _i^{*}} = 0$
), then there will be no bias. Thus, we are concerned about scenarios where treatment effect heterogeneity exists and is correlated with survey response eagerness. Equation (1) shows that if eagerness to respond to surveys is related to the individual-level treatment
![]() $\tau _i$
in a given experiment, these surveys result in biased estimators for population-level treatment effects. In other words, the results may not generalize to the target population. However, and perhaps more importantly given our findings, if there is limited or no treatment effect heterogeneity, then results would generalize, even in unrepresentative samples.
$\tau _i$
in a given experiment, these surveys result in biased estimators for population-level treatment effects. In other words, the results may not generalize to the target population. However, and perhaps more importantly given our findings, if there is limited or no treatment effect heterogeneity, then results would generalize, even in unrepresentative samples.
4. Comparing Treatment Effects among Eager and Reluctant Respondents
As Equation (1) makes clear, bias occurs when there is a correlation between sample selection and treatment effect moderators. Another way of stating this is that bias occurs when treatment effects are different among eager and reluctant respondents. In this section, we turn to an empirical evaluation of this potential for bias. For each of the 50 studies in our data, we identify a main treatment effect of interest and estimate this effect separately among eager respondents, defined as those who agreed to participate after the initial contact, and among reluctant respondents, defined as those who initially declined to participate but agreed only after the more intensive NRFU recruitment. In essence, we are treating this NRFU indicator as
![]() $R_i$
in our bias decomposition in Equation (1). (Replication code and data are available on the Harvard Dataverse; Moniz et al. Reference Moniz, Ramirez-Perez, Hartman and Jessee2024. More information about the survey and our approach to defining the main treatment effect in each study can be found in Supplementary Sections E and K.) We divide each dependent variable by its standard deviation in the control group prior to analysis to produce standardized average treatment effect (ATE) estimates, which make comparison across studies more straightforward given the different scales of the dependent variables.
$R_i$
in our bias decomposition in Equation (1). (Replication code and data are available on the Harvard Dataverse; Moniz et al. Reference Moniz, Ramirez-Perez, Hartman and Jessee2024. More information about the survey and our approach to defining the main treatment effect in each study can be found in Supplementary Sections E and K.) We divide each dependent variable by its standard deviation in the control group prior to analysis to produce standardized average treatment effect (ATE) estimates, which make comparison across studies more straightforward given the different scales of the dependent variables.
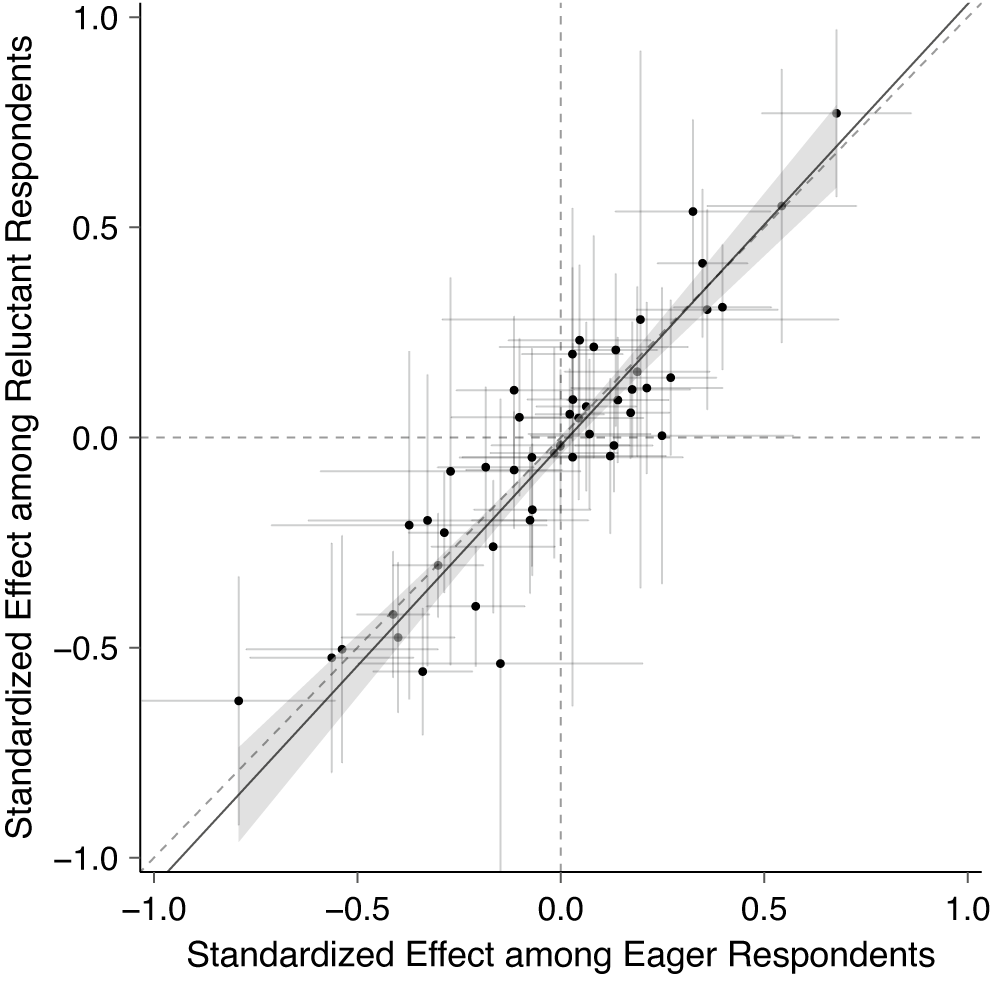
Figure 2 Standardized ATEs among reluctant and eager respondents closely resemble each other. Points show estimated treatment effects estimated separately among eager and reluctant respondents, with 95% confidence interval bars. Solid line shows Deming regression fit and shaded region shows its block-bootstrapped 95% confidence region.
Figure 2 compares these ATE estimates for eager and reluctant respondents in each study along with 95% confidence intervals, with each point representing one of the 50 studies. The solid line shows a Deming regression fit to the treatment effect estimates along with a 95% confidence band, constructed using a block bootstrap.Footnote 1 If effects from eager respondents generalize well to reluctant respondents, we would expect estimates to generally fall along the 45-degree line, indicating that the effect estimates are approximately the same across these two groups. The plot shows a clear positive relationship between the two sets of estimates and the regression fit is quite close to the dashed 45-degree line. The estimated intercept is
![]() $-0.02$
(SE
$-0.02$
(SE
![]() $=$
0.01) and the estimated slope is 1.05 (SE
$=$
0.01) and the estimated slope is 1.05 (SE
![]() $=$
0.07). This suggests that treatment effects among eager and reluctant respondents are nearly identical on average.
$=$
0.07). This suggests that treatment effects among eager and reluctant respondents are nearly identical on average.
Our focus here is on the pattern of treatment effect estimates for eager and reluctant respondents across studies. (Note that these two groups make up roughly similar proportions of the sample within most studies.) While any given study might not be adequately powered to detect smaller differences between these two effects, by looking at estimates across these 50 studies, we can assess whether systematic differences seem to exist between treatment effects for these two groups. Overall, the results in Figure 2 suggest that treatment effect estimates for these 50 studies are very similar among eager and reluctant respondents, indicating little to no correlation between eagerness and treatment effect heterogeneity. Our findings indicate that if researchers relying on a pool of eager respondents invested more effort in recruiting more reluctant respondents, they would not typically estimate appreciably different effects in such samples. While this does not guarantee any specific study would generalize well, which would require study-specific sensitivity analyses (Huang Reference Huang2022), it provides evidence that, on average, there is not any meaningfully large systematic difference in treatment effects estimated among eager as opposed to reluctant respondents.
4.1. Comparing Eager and Reluctant Treatment Effects within Subgroups
Although the results in Figure 2 show no evidence of notable differences between eager and reluctant respondents on average, we also evaluate the similarity between these two sets of estimates within important subgroups of respondents. This analysis sheds light on if there is treatment effect heterogeneity that may be different among eager and reluctant respondents that cancels out or at least is not obvious in the aggregate, but which could still lead to bias through the
![]() $\sigma _{\tau _i}$
term in Equation (1). As argued in Druckman and Kam (Reference Druckman, Kam, Druckman, Greene, Kuklinski and Lupia2011), critics should outline theoretically important moderators that lack support in an experiment when discussing concerns about generalizability. If such important moderators are correlated with observed covariates, our analysis should sheds light on the potential for bias. We conduct the same type of analysis as in Figure 2, estimating ATEs separately among eager and reluctant respondents in each study, but we do this analysis separately for respondents in each of 20 different subgroups defined by important demographic or other characteristics. While we conduct an unweighted analysis, the subgroups we examine are formed using common covariates used in weighting—thus, it sheds light on whether weighted survey experimental results based on eager respondents are truly representative of population effects comprised of a mixture of eager and reluctant respondents.
$\sigma _{\tau _i}$
term in Equation (1). As argued in Druckman and Kam (Reference Druckman, Kam, Druckman, Greene, Kuklinski and Lupia2011), critics should outline theoretically important moderators that lack support in an experiment when discussing concerns about generalizability. If such important moderators are correlated with observed covariates, our analysis should sheds light on the potential for bias. We conduct the same type of analysis as in Figure 2, estimating ATEs separately among eager and reluctant respondents in each study, but we do this analysis separately for respondents in each of 20 different subgroups defined by important demographic or other characteristics. While we conduct an unweighted analysis, the subgroups we examine are formed using common covariates used in weighting—thus, it sheds light on whether weighted survey experimental results based on eager respondents are truly representative of population effects comprised of a mixture of eager and reluctant respondents.
Figure 3 shows the results of the subgroup analyses. These subgroup regressions estimate the relationship between the conditional average treatment effects (CATEs) among eager and reluctant respondents for each subgroup of respondents.Footnote 2 Because of the large number of subgroups being examined, we summarize the subgroup-specific relationships between eager and reluctant treatment effect estimates by presenting the estimated intercept and slope, and the associated 95% confidence intervals, for the Deming regression estimated within each subgroup. Due to a few sets of studies being fielded together on common surveys, we calculate cluster-robust standard errors using a block bootstrap in which we cluster studies conducted on the same respondents. Scatterplots of estimated treatment effects for each subgroup can be found in Supplementary Figure H4. We use Benjamini–Hochberg-corrected confidence intervals to account for the multiple comparisons being made (Benjamini and Yekuteli Reference Benjamini and Yekuteli2005). In each of these subgroup regressions, a slope of 1 and intercept of 0 would indicate that treatment effects within the demographic group are the same for eager and reluctant respondents on average.
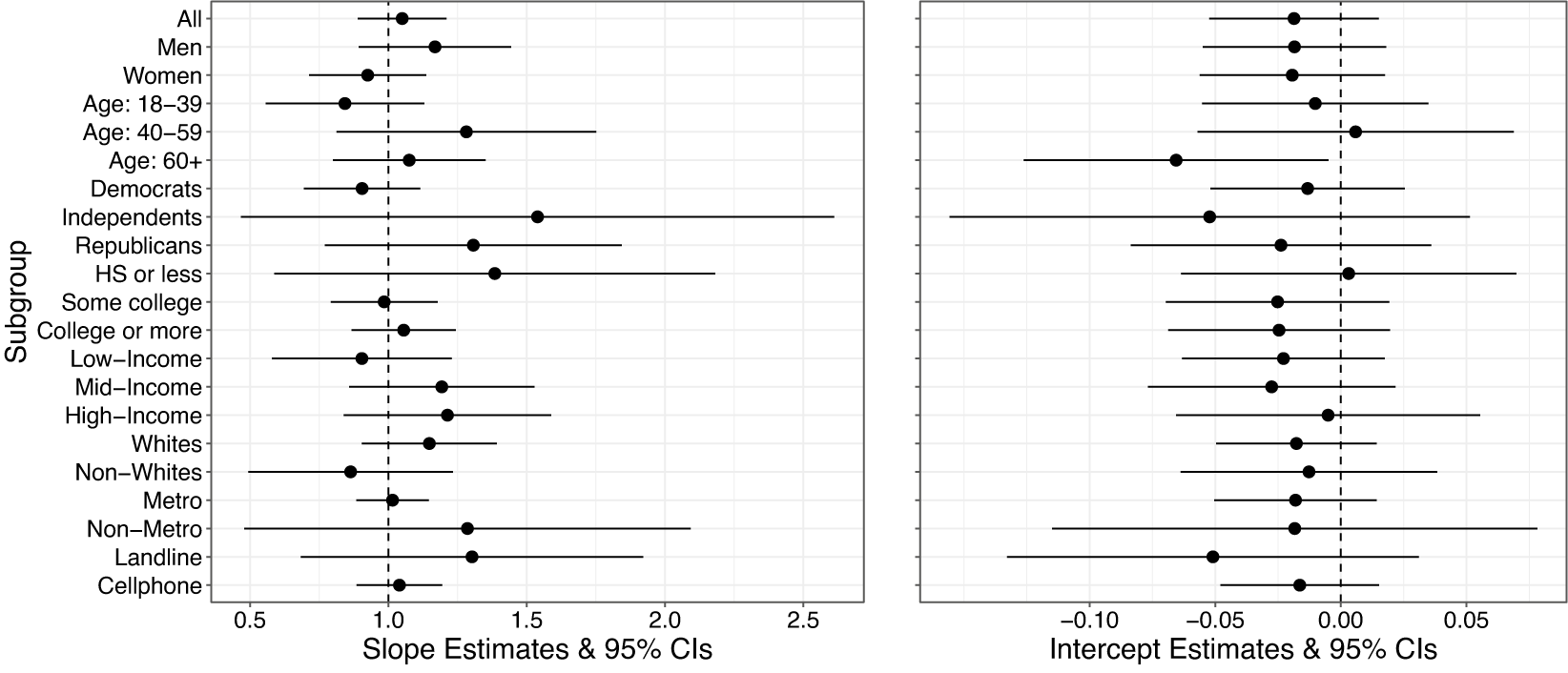
Figure 3 Deming regression estimates relating CATE estimates for eager and reluctant respondents show that effects are similar within subgroups.
As seen in the left panel of Figure 3, the estimated slopes are all fairly close to 1 with the exception of a few estimates that have wide confidence intervals due to small group sizes. For each of the subgroups considered, we fail to reject the hypothesis that the slope is 1. The subgroup intercept estimates, shown in the right pane, are all quite close to 0. Note the scale of the horizontal axis in this pane, with the largest magnitude subgroup intercept estimated as
![]() $-0.05$
standard deviations, which is substantively very small. In only one of the subgroup analyses, do we reject the null hypothesis that the intercept is equal to 0, and in this case (Age:
$-0.05$
standard deviations, which is substantively very small. In only one of the subgroup analyses, do we reject the null hypothesis that the intercept is equal to 0, and in this case (Age:
![]() $60+$
), we reject only narrowly.
$60+$
), we reject only narrowly.
Thus, we do not find strong evidence that subgroup treatment effects differ on average between eager and reluctant respondents in survey experiments even when looking separately within each of these major demographic categories. This suggests that where treatment effect heterogeneity may exist, it does not appear to correlate with eagerness to respond to surveys. We have focused on unweighted analyses, but we note that there is no evidence of substantial treatment effect differences among subgroups defined using common survey weighting variables. This means that effect estimates for eager and reluctant respondents would not be expected to differ among a differently weighted draw among this population that required survey weighting adjustments, although standard errors would be larger (Miratrix et al. Reference Miratrix, Sekhon, Theodoridis and Campos2018). Relatedly, Supplementary Figure H3 displays these subgroup CATE estimates grouped by study rather than by subgroup. In the studies where the CATEs are precisely estimated, there appears to be little meaningful heterogeneity.
A close look at Figure 3 reveals that independents have the largest Deming slope point-estimate of the all the subgroup CATEs (note that this group also has by far the largest confidence interval on its estimate, due to the small sample size for independents relative to other groups considered in the figure). Though its 95% confidence interval crosses 0, the point estimate would suggest that reluctant independent participants exhibit, on average, treatment effects that are around 50% larger magnitude ATE than those for eager independents. Given the political nature of many of the studies funded by TESS, one concern is this pattern may be driven by experiments using politically relevant stimuli. To investigate this, we replicated our main analysis using only political science studies, which represent 29 out of the 50 studies in our overall dataset. We find a similar pattern of no treatment-effect heterogeneity between eager and reluctant participants (Supplementary Figure G1), and estimate a smaller (closer to 1) slope coefficient among Independents using only the political studies than in the entire sample of studies (Supplementary Figure G2).
4.2. A Formal Evaluation of Treatment Effect Heterogeneity
We now turn to a more formal evaluation of observable treatment effect heterogeneity by estimating the individual-level treatment effects,
![]() $\widehat {\tau _i}$
, using a causal random forest model. Recall that there is increased potential for bias when there is increased variation in
$\widehat {\tau _i}$
, using a causal random forest model. Recall that there is increased potential for bias when there is increased variation in
![]() $\tau _i$
, through the
$\tau _i$
, through the
![]() $\sigma _{\tau _i}$
term in Equation (1). By estimating
$\sigma _{\tau _i}$
term in Equation (1). By estimating
![]() $\tau _i$
, we more directly evaluate this potential for bias. We do so using causal random forests, which use random forests to estimate an individual-level treatment effect, rather than to predict the outcome directly, and are pointwise consistent and asymptotically normal (Athey, Tibshirani, and Wager Reference Athey, Tibshirani and Wager2019; Wager and Athey Reference Wager and Athey2018).
$\tau _i$
, we more directly evaluate this potential for bias. We do so using causal random forests, which use random forests to estimate an individual-level treatment effect, rather than to predict the outcome directly, and are pointwise consistent and asymptotically normal (Athey, Tibshirani, and Wager Reference Athey, Tibshirani and Wager2019; Wager and Athey Reference Wager and Athey2018).
Importantly, to capture potential unobserved variables related to response reluctance that might explain treatment effect heterogeneity, we include our NRFU indicator in our causal random forests in addition to the observable characteristics previously described. We use the mean forest prediction parameter as a measure of a forest’s goodness of fit, where a value of 1 suggests that the mean prediction is correct. The average mean forest prediction for our 50 causal random forests is 1.01 (SD
![]() $=$
0.086). We find that the correlations between the estimated individual-level treatment effect and response reluctance is generally small in magnitude, with only three studies having correlations over 0.3 (see Supplementary Figure S4).
$=$
0.086). We find that the correlations between the estimated individual-level treatment effect and response reluctance is generally small in magnitude, with only three studies having correlations over 0.3 (see Supplementary Figure S4).
We then probe why this correlation is weak by evaluating treatment effect heterogeneity within studies, summarized in Table 1. Using our causal random forest predictions, we conduct an omnibus test for heterogeneity within each study based on a “best linear predictor” model for treatment effect heterogeneity (Chernozhukov et al. Reference Chernozhukov, Demirer, Duflo and Fernández-Val2018; Wager and Athey Reference Wager and Athey2018). These tests allow us to capture treatment effect heterogeneity explained by our covariates, including our NRFU indicator. Table 1 shows that 38 of the 50 studies had no statistically significant detectable heterogeneity (“Neither”
![]() $+$
“NRFU only” in Table 1). This suggests that heterogeneity by demographic covariates is uncommon, which aligns with our subgroup analysis above and previous findings in the literature (e.g., Coppock, Leeper, and Mullinix Reference Coppock, Leeper and Mullinix2018).
$+$
“NRFU only” in Table 1). This suggests that heterogeneity by demographic covariates is uncommon, which aligns with our subgroup analysis above and previous findings in the literature (e.g., Coppock, Leeper, and Mullinix Reference Coppock, Leeper and Mullinix2018).
Table 1 An analysis of treatment effect heterogeneity. We conducted an omnibus test provided in the grf R package. We also compared the estimates among eager and NRFU respondents. Most studies show no statistically significant treatment effect heterogeneity in either test (Neither). Ten show evidence of heterogeneity using the omnibus test, but it is not driven by differences between eager and NRFU respondents (Omnibus Only). Two studies show no evidence using the omnibus test, but do display NRFU-specific heterogeneity (NRFU Only), and two others display both general and NRFU-specific effect heterogeneity (Both).

Four studies had heterogeneity related to NRFU (those counted in the columns for “NRFU only” or “Both” in Table 1) estimated by comparing the average predicted individual-level treatment effects for the eager and reluctant respondents. Of those four, only two also had a significant omnibus heterogeneity test in the causal random forest analysis above.Footnote 3 In other words, these heterogeneity tests, conducted at the
![]() $\alpha = 0.05$
significance level, detected NRFU-based heterogeneity (i.e., that which is associated with respondents’ reluctance to respond) in only 8% of the studies considered. This is quite similar to what we would expect to have detected under the null hypothesis of no NRFU-based heterogeneity in any study. Another eight studies exhibited significant treatment effect heterogeneity according to the omnibus test but not to differences between eager and reluctant respondents (“Omnibus Only”), as the average effects of eager and reluctant in these cases did not significantly differ.
$\alpha = 0.05$
significance level, detected NRFU-based heterogeneity (i.e., that which is associated with respondents’ reluctance to respond) in only 8% of the studies considered. This is quite similar to what we would expect to have detected under the null hypothesis of no NRFU-based heterogeneity in any study. Another eight studies exhibited significant treatment effect heterogeneity according to the omnibus test but not to differences between eager and reluctant respondents (“Omnibus Only”), as the average effects of eager and reluctant in these cases did not significantly differ.
Combined, these analyses indicate that treatment effect heterogeneity is rare in the studies we analyze and that detectable general heterogeneity due to differences between reluctant and eager respondents is even rarer. We thus find little heterogeneity by both the demographic variables, which are predictive of survey reluctance, and by survey reluctance itself. Taken together, this suggests that survey experiments fielded primarily to eager respondents are likely to generalize well even to populations consisting mostly of more reluctant survey participants.
4.3. Response Eagerness and Observed Covariates
On average, across these studies, treatment effects appear similar for eager and reluctant respondents both overall and within the demographic categories shown in Figure 3. Therefore, even differentially weighted eager responses would not differ substantially from reluctant respondents or a target population comprised of different proportions of eager and reluctant respondents.
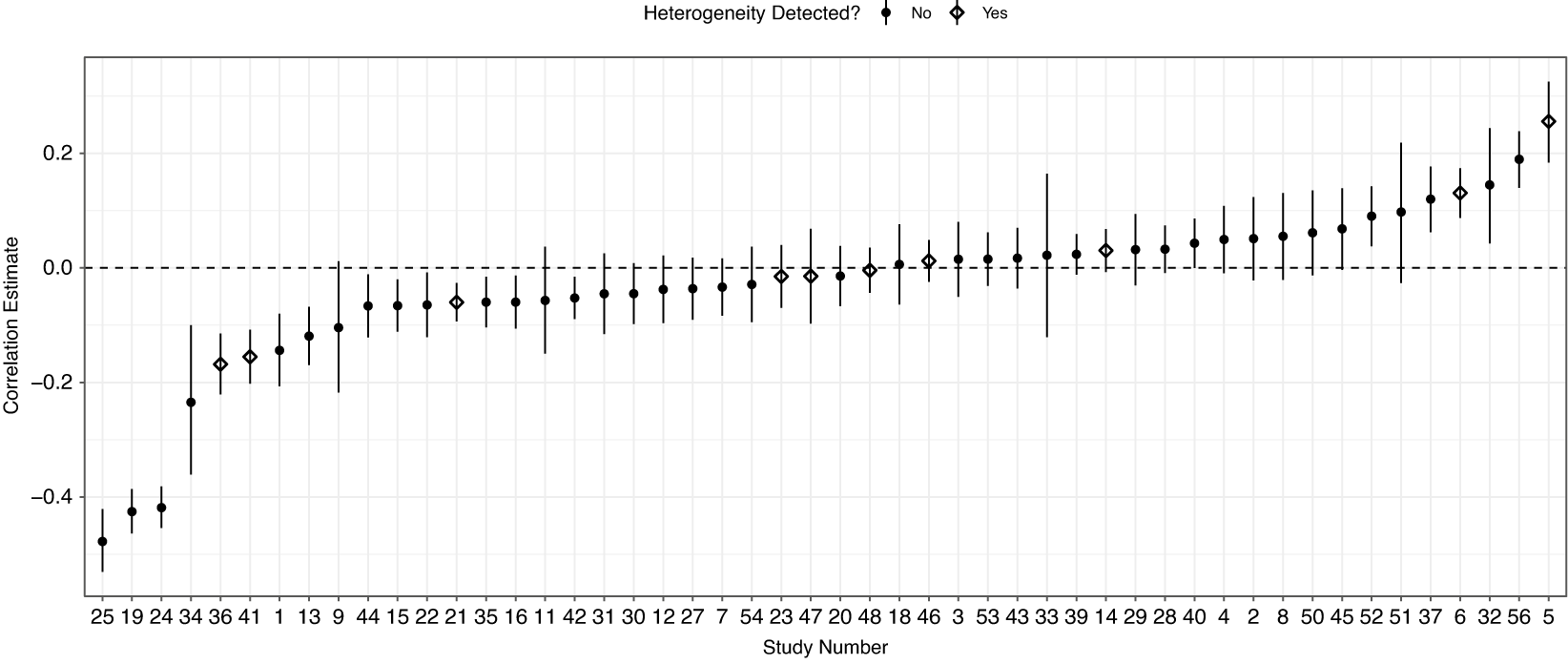
Figure 4 Correlations of individual-level treatment effects,
![]() $\widehat {\tau _i}$
, and propensities of being a reluctant respondent,
$\widehat {\tau _i}$
, and propensities of being a reluctant respondent,
![]() $\hat {\pi }_i^{*}$
, are weak and do not relate to cases with significant treatment effect heterogeneity. The hollow points are cases with significant heterogeneity tests according to omnibus tests from the causal random forest models and solid circles are cases where no significant heterogeneity is detected.
$\hat {\pi }_i^{*}$
, are weak and do not relate to cases with significant treatment effect heterogeneity. The hollow points are cases with significant heterogeneity tests according to omnibus tests from the causal random forest models and solid circles are cases where no significant heterogeneity is detected.
To more directly asses the correlation in Equation (1), we estimate the likelihood of being a reluctant (as opposed to eager) respondent, that is, one who declined to participate in these studies after initial contact, but then agreed after the more intensive NRFU recruitment. We estimate the (normalized) probability of being an NRFU by fitting a random forest using the demographic variables provided by NORC (e.g., age, income, and partisanship). For a full list of the variables used here, see Supplementary Figure H5. In this analysis, we are more directly estimating
![]() $\hat {\rho }_{\hat {\pi }_i^{*},\hat {\tau }_i}$
. If
$\hat {\rho }_{\hat {\pi }_i^{*},\hat {\tau }_i}$
. If
![]() $\pi _i$
can be predicted well, and we do not see evidence of treatment effect moderation among these predictors, then it is unlikely that
$\pi _i$
can be predicted well, and we do not see evidence of treatment effect moderation among these predictors, then it is unlikely that
![]() $\rho _{\pi _i^{*},\tau _i}$
is large.
$\rho _{\pi _i^{*},\tau _i}$
is large.
Using this model, we estimate the correlation between
![]() $\hat {\pi }_{i}^{*}$
and the estimated individual treatment effect
$\hat {\pi }_{i}^{*}$
and the estimated individual treatment effect
![]() $\hat {\tau }_i$
from the causal random forest. Figure 4 plotsFootnote 4 these estimated correlations by study.Footnote 5 The first takeaway is that the correlations are typically small in magnitude. All but three are less than 0.3. The second takeaway is that the distribution of the hollow points is fairly evenly across the distribution. This suggests that there is no clear relationship between treatment effect heterogeneity and having a strong correlation between individual-level treatment effect and survey reluctance. If all the hollow points had been at the left or right ends of the plot (large in magnitude), that would have been evidence of a strong relationship between survey eagerness and treatment effect heterogeneity.
$\hat {\tau }_i$
from the causal random forest. Figure 4 plotsFootnote 4 these estimated correlations by study.Footnote 5 The first takeaway is that the correlations are typically small in magnitude. All but three are less than 0.3. The second takeaway is that the distribution of the hollow points is fairly evenly across the distribution. This suggests that there is no clear relationship between treatment effect heterogeneity and having a strong correlation between individual-level treatment effect and survey reluctance. If all the hollow points had been at the left or right ends of the plot (large in magnitude), that would have been evidence of a strong relationship between survey eagerness and treatment effect heterogeneity.
While there is little evidence of observable heterogeneity related to reluctance, unbiased estimation of
![]() $\rho _{\pi _i^{*},\tau _i}$
requires we have included all relevant factors, and there remains the possibility that within some other covariate not examined here the treatment effects for eager and reluctant respondents show meaningful differences on average, which would lead to bias. Note, however, that such a confounding moderator would need to be nearly orthogonal to our observed demographic covariates, as we do not find meaningful heterogeneity when using such observed covariates even as a proxy for such a moderator. Even if such a confounding moderator exists, though, in order for such treatment effect heterogeneity based on unobserved covariates to result in meaningful bias in estimating the population average treatment effect, the unobserved covariates would also need to be related to response eagerness. This would be true conditionally after weighting adjustment as well.
$\rho _{\pi _i^{*},\tau _i}$
requires we have included all relevant factors, and there remains the possibility that within some other covariate not examined here the treatment effects for eager and reluctant respondents show meaningful differences on average, which would lead to bias. Note, however, that such a confounding moderator would need to be nearly orthogonal to our observed demographic covariates, as we do not find meaningful heterogeneity when using such observed covariates even as a proxy for such a moderator. Even if such a confounding moderator exists, though, in order for such treatment effect heterogeneity based on unobserved covariates to result in meaningful bias in estimating the population average treatment effect, the unobserved covariates would also need to be related to response eagerness. This would be true conditionally after weighting adjustment as well.
To assess the plausibility of hypothetical unobserved confounders having these properties, we examine the degree to which eagerness to respond is predicted by our observed covariates and, by implication, how much remaining variation exists in response eagerness after accounting for these variables. Because this analysis involves pooling samples across all of the studies in our data, any two studies may contain a small number of the same respondents. Furthermore, the respondent identifiers in these data are not the same across studies, preventing us from directly dropping such duplicate observations. As described in Supplementary Section B.1, we drop any observations that are identical on a series of demographic variables that are included in all studies, which results in a new sample size of 34,799 for the analyses below.
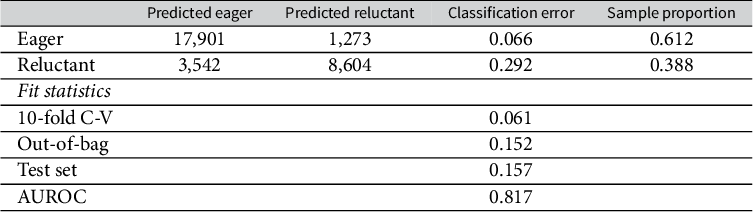
The model performs well, correctly classifying 84.3% of respondents in the out-of-sample test set and accounting for most of the variance in the test set (AUROC = 0.817). See Table 2 for the confusion matrix and additional model fit statistics. Variable importance plots are shown in Supplementary Figure H5. Income contributes the most to model accuracy, with religious attendance, party ID, and age also adding significantly to the model.
Table 2 Confusion matrix showing the number of correctly and incorrectly predicted observations by the random forest model on the training set (based on out-of-bag data). Below it are the error rate for the training sample 10-fold cross-validation parameter-tuning procedure, training sample out-of-bag error rate for the tuned model on the training set, and the out-of-sample error rate on the test set. Error rates are proportions of cases predicted incorrectly. AUROC is the area under the ROC curve, which plots the true positive rate against the false positive rate.
The fact that these covariates predict response reluctance well should mitigate, but not eliminate, fears about confounding in the generalizability of effect estimates to broader populations containing more reluctant respondents from samples that consist overwhelmingly of eager respondents. Because this relatively small set of observed covariates predicts response reluctance fairly accurately, there is not a lot of remaining variation for a hypothetical unobserved confounder to explain in response propensity. To cause significant bias, treatment effect heterogeneity based on an unobserved covariate would have to be extremely (perhaps implausibly) large in order to meaningfully impact estimates of the population average treatment effect. Future work could investigate the robustness of individual studies to such unobserved factors.
5. Discussion
In the field of survey experiments, representative probability samples are often viewed as the gold standard for learning about average treatment effects in a population. But in recent years, response rates even to these high-quality (and expensive) surveys have dropped precipitously. Today it is common for less than 10% of people who are asked to participate, and sometimes far less, to actually end up taking these surveys. This raises the question of whether respondents to these surveys are different from those who do not respond in ways that might bias treatment effect estimates away from the true average effect in the broader population of interest. To put it differently, if responding to these surveys is so unusual among members of the population, are we only learning about treatment effects within an unusual segment of the population?
Previous work has asked whether moving from probability samples to less representative convenience samples, which consist overwhelmingly of very eager respondents, produces similar estimates. Our study instead asks whether effect estimates are similar when moving in the other direction, generalizing toward the large fraction of the population that consists of more reluctant respondents. To investigate this question, we rely on a set of 50 survey experiments covering a wide range of social science topics. Our approach leverages a unique respondent recruitment method that allows for the identification of eager and reluctant respondents. We find that, on average, the estimated treatment effects are quite similar for eager respondents as for reluctant ones. We also find that within a variety of different demographic subgroups, the treatment effects for eager and reluctant respondents do not show meaningful differences on average. While we focus on comparing unweighted eager and reluctant groups, our analysis also sheds light on survey experiments that employ survey weights to address nonresponse. Most survey weights are constructed using demographics similar to those analyzed in our study, and the lack of conditional treatment effect differences indicates that any differentially weighted samples using survey weights constructed based on these demographics would most likely not exhibit overall differences in point estimates and would likely have inflated standard errors (Miratrix et al. Reference Miratrix, Sekhon, Theodoridis and Campos2018).
We emphasize that our results suggest that social science survey experiments conducted on eager respondents who are overrepresented in surveys generalize well to a deeper pool of more reluctant respondents, yet we cannot empirically shed light on whether the same would be true for nonrespondents. We note, however, that the degree to which response propensity between eager and reluctant respondents captured by our NRFU indicator is correlated with an indicator for full nonresponse, our analysis sheds light on the potential for bias. For there to be significant bias among those individuals not represented in our analysis, there would need to be a theoretically relevant moderator that is highly predictive of treatment effects in social science experiments, has no support in the NORC panel, is nearly orthogonal to the included observed covariates, and is strongly predictive of full nonresponse. If such a theoretically moderator were correlated with our NRFU indicator or observable covariates, we would have captured that heterogeneity with our analysis. While it is possible that such a theoretically relevant moderator exists, following Druckman and Kam (Reference Druckman, Kam, Druckman, Greene, Kuklinski and Lupia2011), we believe that “the burden, to some extent, falls on an experiment’s critic to identify the moderating factor and demonstrate that it lacks variance in an experiment’s sample.” Additionally, we note that our goal was to assess generalizability broadly speaking in the social sciences, but researchers concerned about such bias within any specific experiment should evaluate the plausibility of confounding moderators using sensitivity analyses (Huang Reference Huang2022). A fruitful avenue of research could systematically probe the potential for such bias when generalizing to nonrespondents.
Concerns about generalizability are not limited to survey experiments, and extend broadly to other domains such as lab, field, and medical trials (e.g., Druckman and Kam Reference Druckman, Kam, Druckman, Greene, Kuklinski and Lupia2011; Egami and Hartman Reference Egami and Hartman2023; Stuart et al. Reference Stuart, Cole, Bradshaw and Leaf2011). The approach we use here could also be used to learn about generalizability in non-survey experiments. In particular, we emphasize that what made our study unique was that we had a large number of reluctant respondents, and a way to identify them within our studies. Future research in other domains should focus on making sure to recruit reluctant respondents that can also be identified within the experimental trial.
Our findings suggest that the types of experiments studied here would produce similar results whether conducted on primarily eager respondents, or on a mixture of eager and reluctant respondents, and thus are generalizable to broader or different populations. We emphasize that they do not suggest, however, that survey experiments are necessarily externally valid. Debates surrounding abstraction, mundane realism, operationalization and measurement, and other forms of treatment validity are open and important concerns that bring into question the external validity of experiments, separate from the generalizability questions we examine here. In light of our findings, we believe that many critics’ concerns about survey experiments may be more closely related to concerns about treatment validity than about the representativeness of the experimental sample itself.
Taken together, our results suggest that experimental findings based on probability samples, even in the modern era of very low response rates, provide reasonable estimates of population average treatment effects for the treatments and outcomes typically measured in social science experiments, at least among individuals who can be incentivized to participate in surveys. Response eagerness does not seem to moderate treatment effects to a meaningful degree across the broad set of studies we analyze. The studies analyzed include eager respondents who were recruited using incentives and approaches that are commonly used in many surveys and reluctant respondents only agreed to participate after recruitment that was much stronger than typically used in standard surveys, even those in higher-quality probability samples. This means that although we cannot directly estimate treatment effects for those who still refuse to participate even after intense (NRFU) recruitment, our data allow us to compare respondents over a much wider range of eagerness/reluctance than is commonly found in modern survey samples. Combined with results showing that effects estimated in convenience sample surveys do not differ systematically from probability sample surveys, we contribute to the evidence that survey experiments among eager respondents more broadly appear generalizable to a deeper pool of survey respondents.
Acknowledgements
We thank Adam Berinsky, Mike Findley, John Gerring, Chad Hazlett, Melody Huang, Connor Jerzak, Neil Malhotra, and participants in the University of Texas Department of Government’s Methods workshop and the 2022 PolMeth Summer Meeting for helpful comments. Jamie Druckman in particular provided invaluable advice and support. Dan Costanzo and the staff at NORC provided amazing help and advice throughout the project. We thank Carlos Carvalho and the Salem Center for Policy at the University of Texas McCombs School of Business for providing funding.
Funding Statement
This research was supported by a grant from the Salem Center for Policy at the University of Texas McCombs School of Business.
Competing Interests
The authors declare no competing interests.
Data Availability Statement
Replication code for this article has been published in Political Analysis Harvard Dataverse at https://doi.org/10.7910/DVN/N15MSX.
Supplementary Material
For supplementary material accompanying this paper, please visit https://doi.org/10.1017/pan.2024.8.









