Roll-call voting under random seating assignment

Abstract

Social connections between individuals can profoundly impact their political behavior. A growing body of research on legislative politics examines how spatial proximity to fellow legislators affects voting behavior within the institution. However, studies that examine this question often suffer from a fundamental identification problem in which proximity effects may reflect actual behavioral diffusion between members or, instead, homophily, in which legislators of a similar political feather flock together. We overcome this observational equivalence by exploiting a unique random seating lottery for seating assignments in the world's oldest existing parliament, Iceland's national legislature, Alþingi. Utilizing this naturally occurring randomization, we employ spatial analyses of more than 20,000 estimates of spatial dependence and find little evidence that seating proximity leads to similar voting behavior by members in this legislative context.

1. Introduction

A core motivation of the social sciences is to better understand interactions between various actors and how these interactions shape behavior. In political science, for example, scholars have examined how the proximity of states affects their propensity for conflict (Most and Starr, 1980), how policy diffusion is spurred by peers (Simmons and Elkins, 2004), and how social context influences electoral behavior (Huckfeldt and Sprague, 1995). Each of these studies finds that spatial proximity promotes interactions between actors and influences their behavior as a result.

For many years, the field of legislative studies has been interested in the effects of spatial proximity, where behavioral diffusion could have substantive effects on policy and, furthermore, provide insight into the role of discourse in policy-making. Indeed, the idea that legislative seating arrangements influence members’ relationships and behavior has a long pedigree. Winston Churchill, for example, believed that the seating arrangements in a legislature were influential in shaping voting patterns, arguing that the House of Commons promoted inter-party conflict and a two-party system by seating government and opposition members of parliament (MPs) at opposite sides of the chamber (Goodsell, 1988: 295).

There is some anecdotal evidence to suggest that legislative seating arrangements matter. US senators have identified seating patterns as important influences on their voting behavior. For example, Senator Robert Menendez (D-NJ) praised Kirsten Gillibrand (D-NY) for leveraging their proximity to influence his behavior on health care legislation for 9/11 first responders, stating “Kirsten Gillibrand sits next to me on the floor of the United States Senate, and I got to tell you something, if she grabbed me one more time and said, this is where we are on the 9/11 bill, this is where we are on the 9/11 bill, can you talk to this one, can you talk to that one? She was—you know, really incredible, incredibly driven.”¹ Similarly, Joe Biden reflected on the impact of sitting next to Senator Ernest “Fritz” Hollings (D-SC) for over three decades in the Senate: “I learned sitting by his side for 32 years … not only what makes this man tick … what he cares about—what he's willing to fight for … but you get a glimpse of a man's soul as well as his intellect and his passion.”²

The effects of spatial proximity on legislative behavior have been examined in a more systematic manner in the literature on legislative politics and interpersonal influence (see, e.g., Young, 1966; Caldeira and Patterson, 1987; Masket, 2008; Rogowski and Sinclair, 2012). The conclusion of most of these observational studies is that spatial proximity influences legislative behavior, as legislators who sit, live, or work near each other are more likely to vote together than legislators that sit further apart (but see Rogowski and Sinclair, 2012).

Observational studies, however, suffer from a fundamental identification problem. On the one hand, the correlation between spatial proximity and roll-call voting may indeed be due to behavioral interactions between neighboring legislators. On the other, it may be due simply to homophily, as birds of a feather choose to sit, live, or work near each other. Distinguishing between these two explanations is much more difficult and less plausible without random assignment of spatial locations. Random assignment of locations such as legislative seating is extremely rare, however, and as a consequence, despite several decades of research supporting the argument that proximity influences legislative behavior, there is more to learn.

In this article we exploit a rare case of random legislative seating assignment to distinguish between effects from behavioral interaction and patterns arising from homophily. Specifically, we employ roll-call voting data from Iceland's Alþingi. Since 1916, members of Alþingi have been randomly assigned seats by lottery.³ The features of this lottery are particularly attractive for a study of spatial proximity's effects on roll-call voting. At the beginning of each session of Alþingi, members (in alphabetical order by first name) choose numbered balls at random, with the number of the ball corresponding to a particular seat in the legislature.⁴ Members then retain this seat for the remainder of that legislative session.⁵ With seat-swapping exceedingly rare and identifiable, Alþingi provides us the best possible, real-world randomized mechanism for examining the effects of spatial proximity on roll-call voting behavior. With homophily eliminated as a possible explanation, a finding that spatial proximity predicts voting behavior in Alþingi would be evidence in support of the spatial diffusion of legislative behavior. One possible implication of the absence of such spatial dependence in a randomized setting, in contrast, is that previous findings of dependence in other legislatures may be epiphenomenal, reflecting an aspatial process in which like-minded legislators have simply chosen to sit together. Alternatively, it may be that other characteristics of Alþingi make such a relationship less likely. In any case, we believe that it is important to examine this case as scholars build, incrementally, toward a more comprehensive understanding of peer effects in legislatures. In short, we believe that the random assignment of seating in Alþingi allows us to overcome the identification problem inherent in previous studies and thereby add to our understanding of social interaction within legislatures.

Our article is structured as follows. In the next section we examine insights from previous, observational studies of interpersonal influence in legislatures. We then turn to a discussion of Alþingi before presenting our spatial methods and data. This is followed by a discussion of our more than 20,000 spatial analyses and a comparison of our findings with Saia's (2018) previous work on Alþingi. The final section discusses implications and concludes.

2. Interpersonal influence in legislatures and beyond

It should come as no surprise that legislators speak of being influenced by fellow legislators nor that they take cues from these members. Legislators face a host of issues and are called upon to vote hundreds of times each year, making it impossible for any individual to stay fully apprised of all the matters that will come before them. The complexity of the policymaking process, and the attendant uncertainty, is one reason for the existence of institutionalized committees that foster expertise and informative signaling (Krehbiel, 1991). In his influential work on roll-call voting in Congress, Kingdon (1989) argues that committee experts are integral sources of information for uncertain legislators (see also Box-Steffensmeier et al., 2015). Co-partisans, state delegation colleagues, and party leaders also provide cues about how to vote, particularly on less salient issues (Matthews and Stimson, 1975; Kingdon, 1989).

Beyond the “professional sources” (experts, co-partisans, and members with similar district or state constituencies) emphasized by these studies, scholars have also argued that an important factor in legislative decision making is much more personal in nature, consistent with the statements by Menendez and Biden. That is, the interpersonal relationships among legislators and the networks in which members are embedded are likely to affect the choices they make. Political scientists have recognized this for some time. In his classic work on the antebellum Congress, Young (1966) identifies congressional boarding houses as a key source of legislative networking that produced unique voting blocs in Congress (but see Bogue and Marlaire, 1975). Minozzi and Caldeira (2021) re-examine living arrangements in the 19th century US House of Representatives and provide an exhaustive analysis spanning 60 years that takes great pains to carefully identify proximity effects.

In a related vein of research, Patterson (1959) and his collaborators examine the patterns and implications of interpersonal networks in the Iowa and Wisconsin legislatures. Caldeira and Patterson (1988) argue that friendship and respect are key sources of legislative initiative and action. In other work, Caldeira and Patterson (1987) consider three sources of friendship ties in the legislative context: homophily (that like-minded members are naturally drawn together), shared attributes, and spatial proximity. As they note, “seating arrangements are not mere housekeeping items for legislatures; on the contrary, they have a good deal to do with the nature of social relationships and the cohesion of parties within the legislature” (969). They find that the most significant proximity effect accrued among deskmates, as legislators were much more likely to identify the legislator with whom they shared a desk as a friend than they were non-deskmates. Also in this spatial vein, Patterson (1972) uncovers a link between seating and party cohesion in Congress by tracing partisan seating in the US House and Senate from the Civil War through the first decade of the 20th century. Concurrent with the well-known rise in polarization over that time span, legislators in both chambers adopted a greater degree of intra-party seating cohesion by the turn of the century. While Patterson's aggregate-level account is suggestive of a link between seating and voting behavior, the causal mechanism is not clearly specified or assessed.

More recently, Masket (2008) examines the effect of being deskmates on agreement scores in the California Assembly from 1941 to 1975 and finds a consistent positive relationship between seating proximity and similarity in voting. In their study of network effects in congressional voting, Cohen and Malloy (2014) examine seating proximity in the Senate as one among many indicators of interpersonal connectivity in the 101st to 110th Congresses (1989–2008). While most concerned with the effect of alumni networks and politicians’ links to industry, they, like Masket, find a positive effect of proximity on roll-call voting similarity in their analysis.

In a particularly innovative study, Rogowski and Sinclair (2012) employ the US House office lottery to examine the effects of House office location on legislative behavior. At the beginning of each Congress, new members draw numbers in the House office lottery and subsequently pick their office locations from the remaining available locations in the order drawn in the lottery. Thus, members who randomly draw lower numbers in the lottery are able to choose from a broader set of available offices than those drawing higher numbers. Using these randomly drawn lottery numbers as an instrumental variable, Rogowski and Sinclair find that House office proximity does not influence legislative behavior. Ferber and Pugliese (2000) likewise find that proximity in office location has no effect on communication patterns in the New York State Assembly. And while finding that seating proximity on the floor is positively related to communication, they conclude that much of this proximity effect is due to homophily.⁶

Importantly, none of these studies employs a fully randomized set of seat assignments and thus none can identify whether any effects of spatial proximity on legislative behavior are due to behavioral diffusion or homophily. For example, the Speaker in the California Assembly chooses where members sit (Masket, 2008: 304). In the sessions of the US Congress examined by Cohen and Malloy (2014), senators choose by class where to sit, affording extensive opportunities for homophily to drive similarity in floor behavior. Although the Wisconsin and Iowa legislatures examined by Caldeira and Patterson (1988) employed lotteries, neither resulted in a random set of seat locations. Rather, these lotteries induced a constrained choice process, with members drawing lottery numbers but then being free to select their seats from those still available. Members had ample opportunities to choose to sit next to friends, particularly those who drew lower lottery numbers. This lottery process is identical to the House office lottery examined by Rogowski and Sinclair (2012). Thus, while these studies examined whether spatial proximity influences legislative behavior, lacking a random seating assignment mechanism, none is able to identify fully whether proximity effects reflect behavioral diffusion or homophily.

Although studies of random seating assignment are almost non-existent in the legislative politics literature, there has been considerable interest in other disciplines in random spatial assignments. These studies, like ours, are motivated by the identification problem inherent in identifying how spatial proximity affects behaviors of various types. Distinguishing between direct behavioral influence among neighbors versus homophily is impossible without knowing how actors are selected into their spatial locations (see Manski, 1993). One particularly rich literature on peer effects examines dormitories. These studies exploit the random assignment of students in college dormitories to examine how spatial proximity influences behaviors and outcomes both in college and in subjects’ career paths. These studies find that spatial proximity to randomly assigned neighbors influences students’ grade point averages and decisions to join social organizations such as fraternities (Sacerdote, 2001), employment outcomes (Marmaros and Sacerdote, 2002), racial attitudes (Shook and Fazio, 2008), and interracial friendships (Baker et al., 2011). In short, while there is substantial evidence that randomly assigned spatial proximity influences a variety of behaviors, we do not know whether such effects extend to political elites. Nor do we know whether they extend to expressly political behaviors, such as legislative voting behavior.

3. Alþingi

Founded in 930, Iceland's Alþingi is the oldest existing parliament in the world. A unicameral legislature since 1991, Alþingi currently has 63 members, although this includes nine to twelve cabinet ministers and the speaker, who usually are MPs. The MPs sit in a hemicycle with cabinet ministers and the speaker sitting in specially designated seats in front of the chamber, see Figure 1.⁷ While formally a semi-presidential system, Iceland has functioned as a “normal” parliamentary system for the most part since gaining independence in 1944. Government coalitions are the norm, the government has a fairly firm hand on the legislative agenda, and party discipline is high. MPs can propose legislation, but, as in most parliamentary systems, the success rate of private member bills is low. Overall, legislative politics are dominated by the political parties and Alþingi's weakness and lack of independence are often bemoaned by MPs—particularly when they find themselves in the opposition.

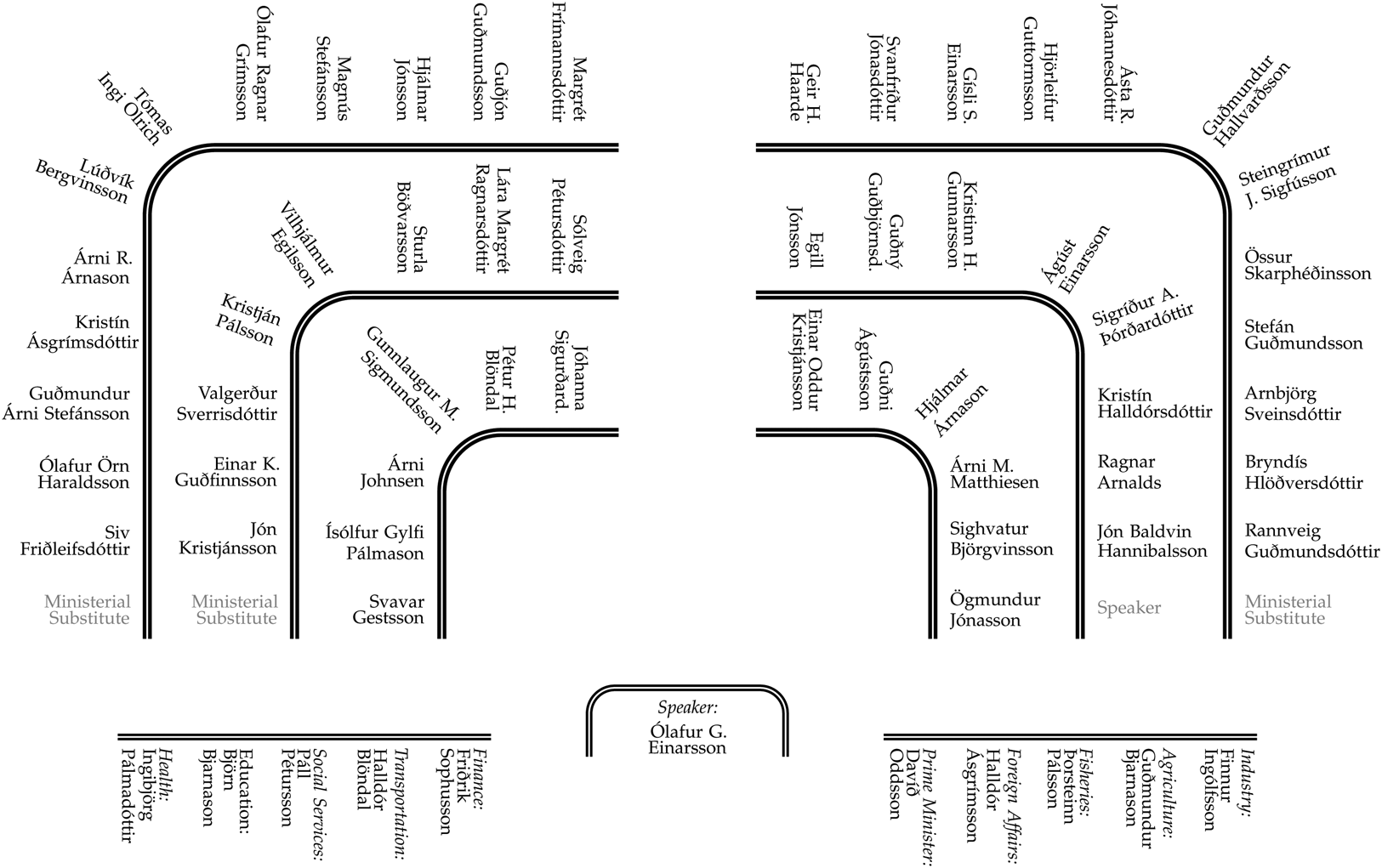
Figure 1. Alþingi seating chart (119th session).

The Icelandic party system can be described as having a core of four major parties whose roots extend back to the beginning of the republic, although some of them have merged with other parties and suffered from splits. We provide an overview of the parties and coalitions as well as a representative look at our multidimensional scaling of the voting record in Appendix A of the Supporting Information (SI).

3.1 Chamber configuration and seat assignment

The Alþingi chamber is located in the Parliament House, or Alþingishúsið, a small building completed in 1881 when Reykjavík's population was less than 4,000 people. As a consequence of its location in a small structure, the Alþingi chamber itself is quite small physically at only 971 square feet, which is roughly equivalent to half the physical footprint of a typical free-standing suburban Starbucks store.⁸ The chamber is all the more cramped today because the previously bicameral Alþingi became a unicameral legislature in 1991—a chamber designed for only 36 members in the lower house at the time it was constructed now seats considerably more legislators. As a result, members of Alþingi sit quite close to each other, as can be seen in the photo of the chamber in Appendix B of the SI. All else equal, we would expect greater interaction between neighboring legislators in such a small chamber compared to a larger chamber in which members sit further apart.

At the beginning of each session, the Speaker of Alþingi as well as six vice-speakers are elected, and the MPs participate in a ballot to determine the seating arrangement in Alþingi (Magnússon, 2014). Excluded from the ballot are the members of the cabinet who sit in a row on both sides of the speaker. The MPs draw a numbered wooden ball from a wooden box to determine where they will sit, that is, the number on the ball corresponds to a particular seat in the chamber. The first MP to draw a seat is drawn randomly by the Speaker, using a separate box of balls, but then the draws proceed in alphabetical order. Thus, who the members of Alþingi sit next to is determined at random. There are a handful of examples where MPs have swapped seats following the ballot. But such instances are very rare—in only six annual sessions did MPs switch seats and in each of those sessions there were only one or two swaps. In all instances, the seats were swapped between members of the same party.⁹

3.2 Session and legislative mechanics organization

The electoral term is four years and is split into four legislative sessions with the addition of the occasional short summer session that typically follows elections. Alþingi convenes for a new session at the beginning of October each year and the session runs for about eight or nine months, with business concluded around mid-June—the exception being election years, when the session usually ends in late April (Indridason and Kristinsson, 2018a). MPs spend a considerable amount of time on the floor. Between 2005 and 2010, the chamber convened for between 490 and 886 hours per legislative session.¹⁰ This amounts to meetings being in session for about 15–25 hours per week during the legislative session. Of course, this does not mean that all the MPs are present in the chamber for the whole time.

Legislative proposals in Alþingi undergo three debates. The first debate addresses the bill as a whole and, following the debate, the bill is referred to committee. No vote is taken unless requested by an MP or if there are multiple proposals over the committee of referral. During the second debate, votes are taken on individual sections of the bill as well as amendments. The bill may be referred back to committee if amended. In the third debate, votes are taken on amendments and amended sections as well as on the bill as a whole as amended. The speaker determines how votes are taken, that is, the speaker may, for example, bundle multiple sections of a bill together rather than taking separate votes on each section of the bill. The speaker's decision can be overruled by parliament at the request of a parliamentary party or nine MPs. Parliamentary motions follow a similar procedure. The speaker decides how votes are taken. The speaker can forgo a vote when he or she is confident that there is unanimous consent or a clear majority in Alþingi and if no MP raises an objection. The exception is final votes where a vote must be taken. Votes are recorded electronically—unless there is a malfunction in which case votes are taken by a show of hands. The speaker can, and must if requested by any MP, conduct a proper roll call.

The number of bills and parliamentary motions proposed during the 119th–144th sessions (1991–2015) are shown in Figure 2. In this period, Alþingi considered, on average, 219 bills and 122 parliamentary motions during a regular parliamentary session. The average number of votes taken during those same sessions (shown in Figure 3) was 1,430 with over 2,000 votes taken during a couple of sessions. The great majority of votes are conducted electronically and the votes proceed fairly quickly. For example, Alþingi's yearly report for the 139th session notes that voting took 32 hours, which means each vote required less than a minute and a half on average.¹¹

Figure 2. Number of bills and motions per session.

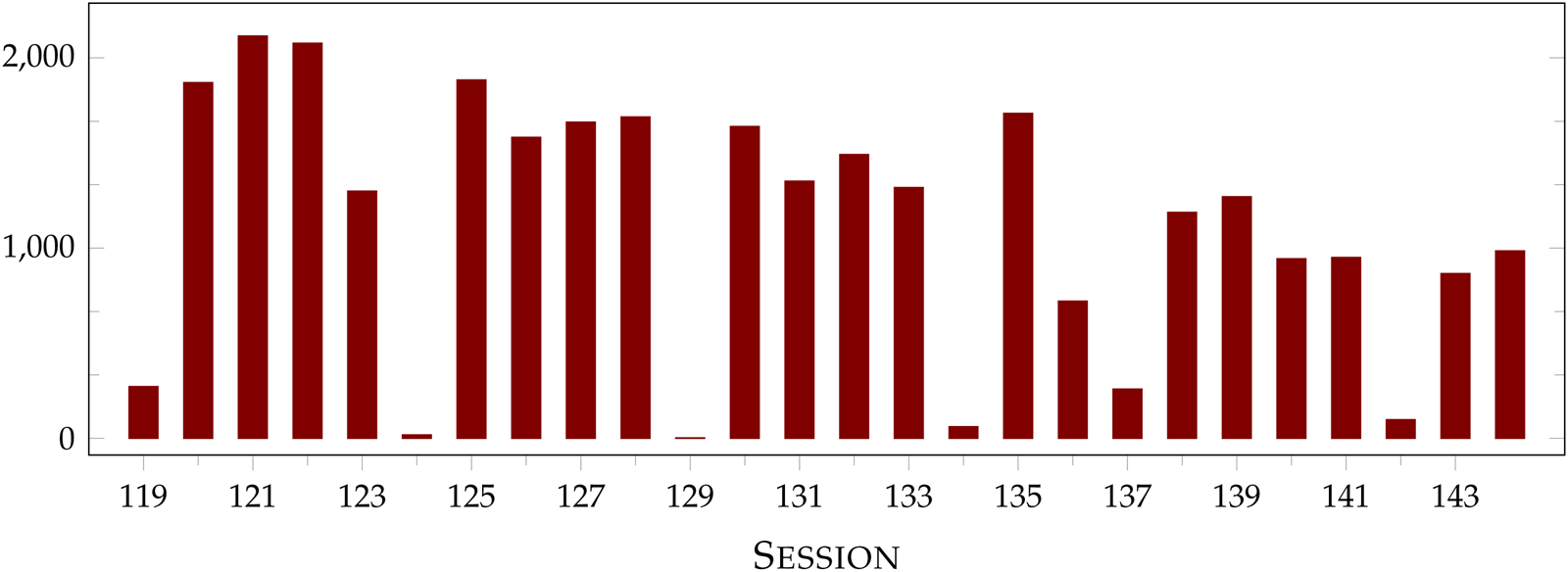
Figure 3. Number of votes per session.

The great majority of legislative proposals are government bills introduced by cabinet ministers. Between 1991 and 2016, 68.4 percent of all bills were government bills, followed by opposition MPs introducing about 20.3 percent, and government MPs accounting for the bulk of the rest.¹² All bills are referred to committee after first reading. Although private member bills account for a fair share of introduced legislation, private member bills are less likely to make it out of committee and are, thus, less likely to be voted on and adopted. Legislative proposals expire at the end of the term and must, therefore, be re-introduced in the following session for continued consideration. In the same time period, opposition MPs introduced 45.5 percent of all parliamentary motions, government MPs introduced 32 percent, and government ministers 22.5 percent.

4. Spatial analysis

With this information about Alþingi in hand, we now turn to the diagnosis and modeling of spatial dependence in peer effects in roll-call voting. If legislators’ seating location predicts their roll-call voting behavior, the result is spatial autocorrelation, or spatial dependence.¹³ Formally, spatial dependence refers to a non-zero covariance between the values on a random variable for neighboring units:

(1)$$\rm{Cov}( y_{i},\; y_{\,j}) = E( y_{i}y_{\,j}) - E( y_{i}) E( y_{\,j}) \neq 0 \rm{~for~} i \neq j,\; $$

where i and j denote spatial locations (Anselin and Bera, 1998: 241–42). Positive spatial autocorrelation exists when neighboring units (e.g., legislators) have similar values on the random variable while negative spatial autocorrelation exists when neighboring units have dissimilar values on the random variable. In our application, we focus on positive spatial dependence because we are interested in identifying whether the similarity in voting behavior of neighboring legislators found in previous studies is due to behavioral diffusion. Positive spatial dependence exists if neighboring members of Alþingi exhibit greater similarity in roll-call voting behavior than would be expected by chance.

4.1 Spatial dependence

The first step in diagnosing spatial dependence in members’ roll-call voting behavior is to estimate this dependence in the absence of covariates. Tests for spatial dependence have been developed for both the global and local levels (see, e.g., Darmofal, 2015). Tests for global spatial dependence diagnose whether the data as a whole exhibit spatial dependence, while local tests diagnose which units (members in our analysis) exhibit spatial dependence. Thus, in our application, a test for global spatial dependence would examine whether legislators as a whole exhibit spatial autocorrelation on a particular roll-call voting measure in an Alþingi session. The principal test for global spatial autocorrelation, and the one we employ in this article, is the global Moran's I. The global Moran's I test is:

(2)$$I = {N\over S}{\Sigma_i \Sigma_j w_{ij}( y_i - \overline{y}) ( y_j - \overline{y}) \over \Sigma_i ( y_i - \overline{y}) ^2},\; $$

with N denoting the number of observations, S the sum of the weights, w _ij an element of the spatial weights matrix W, y _i and y _j the values on the random variable at locations i and j, and $\overline {y}$ the mean of y.

A key component of Moran's I is the spatial weights matrix. This weights matrix denotes which units are to be treated as neighbors of each other and which are to be treated as non-neighbors. This is a critical decision, as only neighbors of unit i are allowed to exhibit first-order spatial autocorrelation with unit i (non-neighbors exhibit only higher-order dependence with i, through neighbors of neighbors). In the weights matrix, neighbors of unit i have non-zero values, non-neighbors of i have zero values, and, typically (as in our analysis), i is treated as a non-neighbor of herself.

We consider three definitions of spatial proximity between members of Alþingi (depicted in Figure 4). The first is an adjacent neighbor definition, in which only legislators who sit on either side of legislator i are considered neighbors of i. The second is a rook neighbor definition, in which members sitting directly in front of or directly behind legislator i are added to the adjacent neighbor definition and are also considered neighbors of i. Our final neighbor definition is a queen neighbor definition, in which members who are sitting to the left or right diagonally in front of or behind legislator i are added to the rook neighbor definition. In other words, the queen contiguity neighbor definition is the most comprehensive of the neighbor definitions and is one in which all legislators surrounding i are treated as neighbors of i.

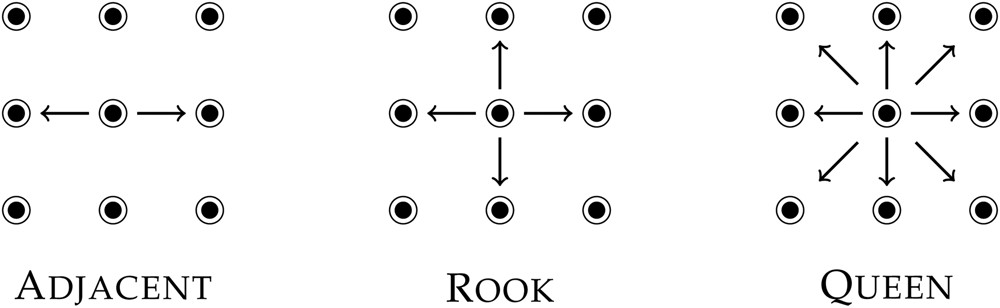
Figure 4. Neighboring locations.

A positive and significant global Moran's I indicates positive spatial dependence. High values cluster with high values at neighboring locations and low values with low values. In our analysis, this would mean, for example, that neighboring members of Alþingi exhibit more similarly liberal (or conservative) voting records than we would expect by chance.

If spatial dependence is diagnosed at the global level, the next step is to examine local spatial dependence to identify which units are spatially autocorrelated with their neighbors and which are spatially independent. Such local spatial dependence can be examined via the local Moran's I. This local Moran's test is a member of a class of statistics known as local indicators of spatial association (LISA) statistics. LISA statistics are tests for local spatial dependence that meet two conditions: (1) they identify which units are autocorrelated with their neighbors and (2) their sum is proportional to a corresponding global measure (Anselin, 1995). The use of the local Moran's I in connection with the global Moran's I allows us to disaggregate the global measure by identifying which units are producing the global finding and which exhibit spatial randomness.

The local Moran's I takes the following form:

(3)$$I_i = {\Sigma_j w_{ij}( y_i - \overline{y}) ( y_j - \overline{y}) \over ( y_i - \overline{y}) ^2},$$

where the notation is identical to that presented for the global Moran's I. A key distinction between the local and global Moran's I tests is that in the former, only the neighbors of i are incorporated in the estimates at each location while in the latter summation occurs over all i.

4.2 Modeling spatial dependence

The tests discussed thus far diagnose spatial dependence at the global and local levels in the absence of covariates. We also, however, want to model peer effects controlling for members’ parties, to determine whether any behavioral influence between neighboring legislators persists in models that account for co-partisans sitting next to each other. Behavioral diffusion, or peer effects, between neighboring legislators are consistent with a spatial lag model that captures the diffusion of behavior between members. Such a model takes the form:

(4)$$y = \rho Wy + X\beta + \varepsilon,\; $$

where y is an N by 1 vector of observations on the dependent variable, Wy is a spatially lagged dependent variable with a spatial weights matrix W, X is an N by K matrix of observations on covariates, β is a K by 1 vector of parameters, ρ is the spatial autoregressive parameter for a spatially lagged dependent variable, and $\varepsilon$ is an N by 1 vector of error terms. The key component of the spatial lag model that sets it apart from non-spatial models is the spatially lagged dependent variable Wy and its corresponding spatial autoregressive parameter, ρ. A positive and significant ρ parameter indicates positive spatial diffusion in which members influence each other to vote similarly. A negative and significant ρ parameter indicates negative spatial autocorrelation in which members’ interactions lead them to vote dissimilarly from each other. And a ρ parameter that is indistinguishable from zero indicates the absence of behavioral diffusion between members.

At first glance, the spatial lag model bears some surface similarities to a temporally lagged dependent variable in time-series analyses. This surface similarity, however, is misleading, as influence flows in only one direction in time-series analyses, from the past to the present, while the spatially lagged dependent variable captures simultaneous spatial dependence. In our application, member i influences her neighbors’ voting behavior while her neighbors also simultaneously influence i's behavior. Indeed, this simultaneous spatial influence is intrinsic to peer effects. But to the best of our knowledge, ours is the first analysis to model this simultaneity in the context of a random seating assignment.

Because of the simultaneity in the peer influences, ordinary least squares (OLS) is a biased and inconsistent estimator of ρ and thus should not be employed to estimate the value of ρ. Instead, maximum-likelihood estimation (ML) that accounts for the simultaneity is typically employed to estimate ρ (see, e.g., Darmofal, 2015). As Anselin and Bera, 1998: 256) show (see also Anselin, 1988: 181–82), the ML estimates for β and σ ² are:

(5)$$\beta_{ML} = ( X'X) ^{-1} X'( I - \rho W) y$$

and

(6)$$\sigma_{ML}^{2} = {( y - \rho Wy - X\beta_{ML}) '( y - \rho Wy - X\beta_{ML}) \over n}.$$

Conditional upon the spatial autoregressive parameter, ρ, the estimates for these non-spatial components are simply the OLS estimates applied to a spatially filtered dependent variable, (I − ρW)y, that is, a dependent variable with the effect of the spatial autocorrelation removed, and the covariates (Anselin and Bera, 1998: 248, 256). Substituting these two sets of ML estimates into the log-likelihood function then produces a concentrated log-likelihood function of the spatial autoregressive parameter, ρ:

(7)$$L_{Lag}^c = -{n\over 2}\rm{ln}\left[{( e_{O} - \rho e_{L}) '( e_{O} - \rho e_{L}) \over n}\right] + \sum_{i}\rm{ln}( 1 - \rho\omega_{i}) ,\; $$

where e _O and e _L are, respectively, the residuals from OLS regressions of y on X and from W _y on X (Anselin, 1988: 181). The ML estimate of ρ is then found from the optimization of this concentrated log-likelihood function (Anselin and Bera, 1998: 256). We employ this ML estimator using the concentrated-likelihood approach for the spatial lag models in our analyses.

5. Data

To our knowledge, votes in the Icelandic Alþingi have not been scaled previously using contemporary political science approaches. Kristinsson (2011) examined party cohesion from 1961 to 2010, noting high levels of both unanimity and party unity, particularly in the period since 1991 that coincides with the introduction of electronic voting and the shift to a unicameral legislature. Kristinsson's findings with respect to party cohesion, as well as the frequency with which many matters are disposed of unanimously, are consistent with legislative voting in parliaments more broadly.

The lack of variation in voting within parties and across Alþingi as a whole poses some potential challenges for us. First, scaling techniques such as NOMINATE rely on non-unanimous votes for estimation. Second, to the degree that votes do not capture underlying variation in preferences due to selection effects inherent in the roll-call record, we may not be obtaining true measures of legislator preferences (Carrubba et al., 2006). In some senses, then, voting in a highly partisan parliamentary system like Alþingi presents a higher hurdle for uncovering evidence of proximity effects in legislative voting.

We examine a number of dependent variables that summarize legislative voting for individual sessions of Alþingi. As described above, the number of votes cast is often well over 1,000, although in shorter sessions there can be considerably fewer votes. Since many votes are unanimous, the scoring of the votes is based on smaller subsets of votes.

Our first measure is the Coalition Support Score, defined as follows. Votes on which a majority of voting MPs in the governing coalition voted in opposition to a majority of voting members outside the governing coalition are identified as coalition votes. Thus for MP_i across coalition votes j:

(8)$${{\it Coalition \;Support\; Score}}_i = 100 \times {\#( {{\it Votes \;with \;Coalition}}) \over {\# ( {\it Coalition \;Votes}) }}.$$

This measure varies in line with the degree of support an MP demonstrates for the coalition and ranges from 0 to 100. As a practical matter, it is “lumpy” at both ends of the distribution, with opposition MPs typically having scores close to 0 and those in the government with scores at or approaching 100.¹⁴

The second measure is the Party Defection Rate, which is similar to the Coalition Support Score but simply defined in terms of party rather than coalition support. As such, it gives us a window into a different behavior that might be tied to seat proximity—the likelihood of defection from one's party. Here we identify a party position for all votes within each party on which a majority of its voting members were decisive (i.e., not tied). A defection occurs when an individual MP votes in opposition to the party's position. As such, for MP_i across party votes j:

(9)$${{\it Party \;Defection \;Rate}}_i = 100 \times {\#( {{\it Defection \;Votes}}) \over {\#( {\it Party \;Votes}) }}.$$

Not surprisingly, defection rates tend to be quite low. Yet there is some variation, albeit less than what we observe in coalition support.¹⁵

In addition to these more conventional voting scores, we estimate both WNOMINATE and IDEAL scores in order to obtain indicators of legislator ideal points. The WNOMINATE approach is grounded in the spatial theory of voting and was developed by Poole and Rosenthal (1997). It assumes a Gaussian distribution for the deterministic component of a legislator's utility function, and is ubiquitous in studies of the US Congress. WNOMINATE allows researchers to generate estimates of legislative preferences that often neatly summarize hundreds of votes or more with a simple indicator based on a single dimension of public policy conflict. For much of US history, a second issue dimension involving racial politics captured some of the remaining variation not picked up in the first dimension of liberal-conservative division over economic issues. Another attractive feature of WNOMINATE is that analysts simply need to fix the polarity of one legislator per dimension estimated in order to orient the policy space. In the analyses presented here, we have estimated WNOMINATE scores on two dimensions for each session of the Alþingi with more than 20 non-unanimous votes. A large proportion of the variation is picked up by the conventional socio-economic left–right dimension. A second dimension, significantly less predictive though still relevant in most sessions, seems to involve a rural–urban divide. On the latter, it is frequently the case that Social Democrats, whose strength lies in urban areas, appear distinct from the Left-Greens, whose roots are more rural and tend to emphasize issues involving the environment and sustainability.¹⁶

In recent years, methodological advances have led to the increased use of Bayesian approaches to ideal point estimation. Clinton et al. (2004), among others, advocate moving away from the classical (or frequentist) approach to scaling legislative voting due to the implicit assumptions embodied in these models. More specifically, the Clinton, Jackman, and Rivers (CJR) approach adopts models based on item response theory (IRT) to uncover estimates of legislator ideal points (IDEAL) that are based on a different parameterization of the utility function, which in this case is quadratic. An advantage of this model is its greater flexibility in contexts in which WNOMINATE will not function, for example, few votes with a small number of legislators. Moreover, it allows scholars to incorporate additional information about the context involving the substance of issues and/or the underlying preferences of legislators.¹⁷ We find that in most cases, the first dimension scores returned by both WNOMINATE and IDEAL are highly correlated with one another, although as previous work has noted (Carroll et al., 2009; Clinton and Jackman, 2009), the IRT approach of CJR seems to be more sensitive to extreme or outlying cases. We are agnostic on which of the two approaches to scaling is preferable, and employ both in our analyses for the sake of completeness.

6. Results

We examine spatial dependence in roll-call voting across these measures for 23 sessions of Alþingi from the 119th session that began in 1995 to the 144th session that ended in 2015. We turn first to our global Moran's I results. We conducted global Moran's I tests for each of our six measures, for each of our three neighbor definitions, for each of these 23 sessions (414 global Moran's I tests in all). In each case we employed a one-tailed test for positive spatial dependence consistent with behavioral diffusion in which neighboring members vote similarly. Figure 5 presents the p-values of these tests graphically.

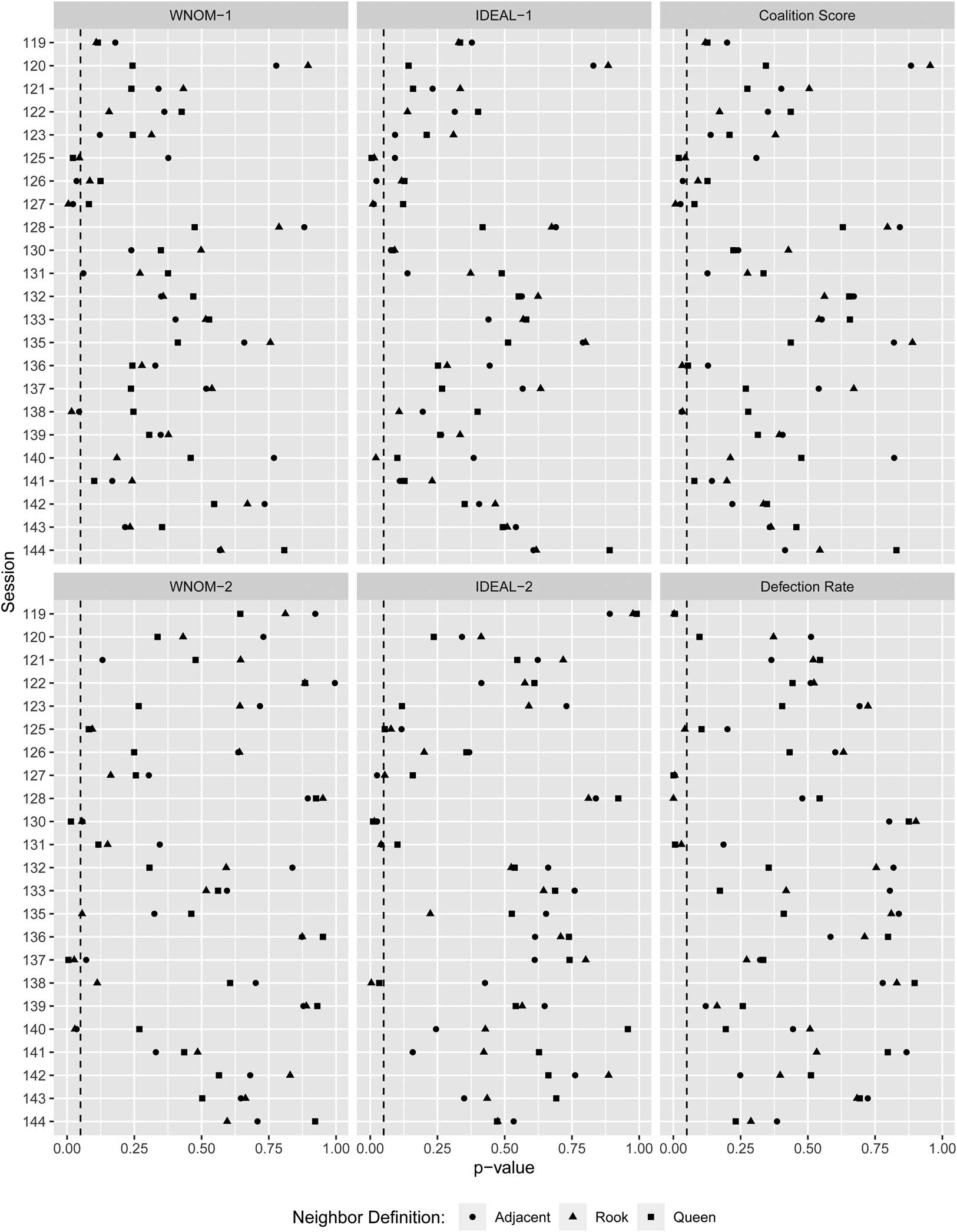
Figure 5. Global Moran's I significance levels.

There is little evidence of systematic spatial peer effects of the type found in previous studies in non-randomized settings. Nearly 90 percent (370 out of 414) of the global Moran's I tests fail to reach statistical significance at a ${\rm p} < {0}.05$ level. In a majority of the Alþingi sessions examined (12 out of 23), none of the 18 global tests are statistically significant at this conventional level.

None of the six roll-call voting measures is particularly prone to detect spatial dependence. In the few tests that reach statistical significance, the number of significant results ranges from a low of five for the second-dimension NOMINATE measure to a high of 10 for the defection rate measure. The rook neighbor definition exhibits slightly more spatial dependence, with 20 significant results—compared with 14 for the adjacent neighbor definition and 10 for the queen neighbor definition. The few significant results are also more or less evenly spread across the combinations of roll-call measures and neighbor definitions. Considering the sessions, it bears noting that there is an unusual pattern of estimated peer effects across the 125th and the 127th sessions. Given the limited evidence for peer effects, it is very unlikely that we would find evidence of peer effects in three adjacent sessions. As far as we can tell, seats were assigned randomly in these sessions as the parliamentary procedures dictate. These sessions took place under the Independence Party's coalition with the Progressive Party (1999–2003) and one possible explanation is that these apparent peer effects are due to some issue on which the coalition parties did not see eye to eye—as is suggested by the fact that the peer effects are far more prominent when the dependent variable measures defection from the coalition's positions than when the focus is on the party line. The overall story, however, is one of little evidence of peer effects when considering global spatial dependence.

The story is much the same when we turn from the global tests to the local tests for spatial autocorrelation. Here we have 21,026 local Moran's I tests for the members in these sessions of Alþingi. In all, only 5 percent of the tests (1,062 out of 21,026) were statistically significant at a ${\rm p} < {0}.05$ level—almost exactly what one would expect to find if there were no peer effects. The fact that there are only a few instances where we fail to reject the null using the local Moran's I test suggests that any evidence of peer effects at the global level, which is quite limited, would have been produced by a very small fraction of the legislators.

It is difficult, of course, to present graphically the results of 21,026 tests across three neighbor definitions, six measures, and 23 sessions. As a result, we focus here on a representative session, the 119th session.¹⁸ Figure 6 presents histograms of the distributions of the p-values for the local Moran's tests for this session for each of the six measures, grouped by the three neighbor definitions. The 0.05 significance level is denoted in this figure by the dashed lines. As we can see, the distributions of the p-values for these tests are located largely to the right of this dashed line. Very few of the local Moran's I tests reached statistical significance in this session, reflective of the overall pattern across the 23 sessions we examined. Just as there was little spatial autocorrelation at the global level, so also was there very little at the local level.

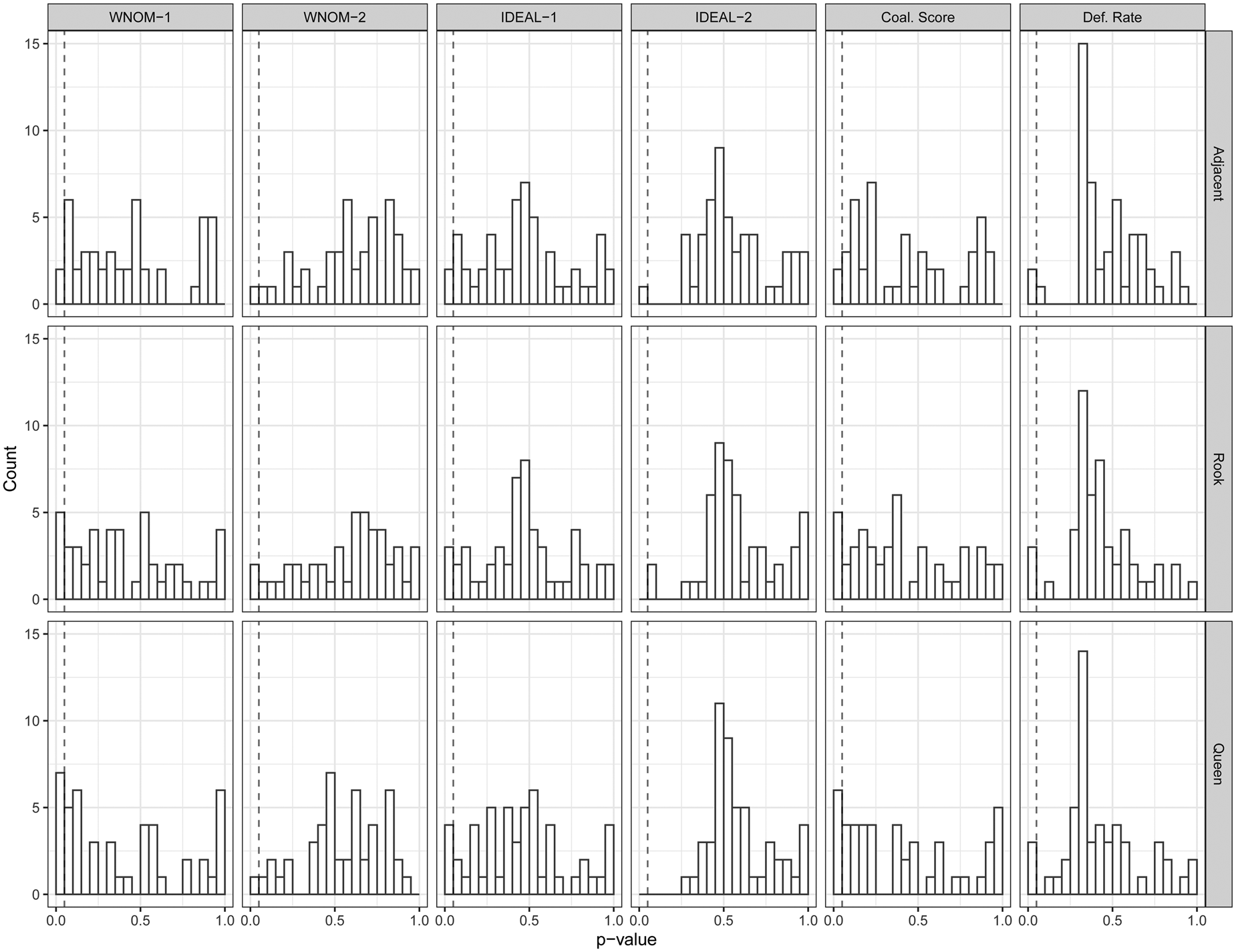
Figure 6. Local Moran's I significance levels for the 119th session.

Finally, we examine the results from the spatial lag models. We estimated spatial peer effects controlling for partisan effects via a set of indicator variables for the parties seated in that session of Alþingi. Once again, there is little spatial dependence. A total of 89.9 percent of the ρ estimates (372 out of the 414 likelihood ratio tests on the ρ parameters) fail to reach statistical significance at a ${\rm p} < {0}.05$ level. These results are presented graphically in Figure 7, closely mirror the results from the global Moran's I tests. Evidence of peer effects is only found in a handful of legislative sessions and, moreover, these appear less robust than one would expect when comparing the different tests.

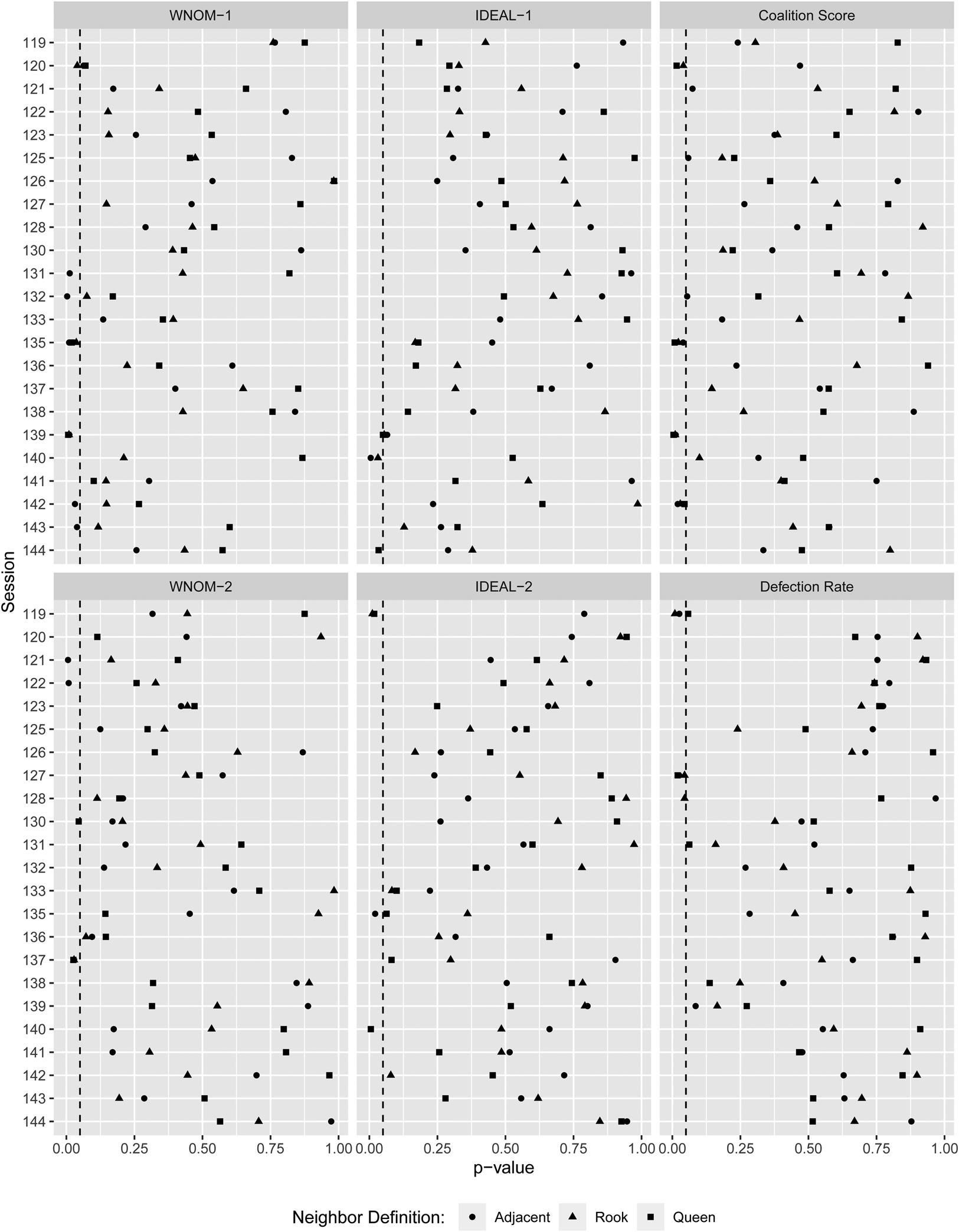
Figure 7. Spatial lag significance levels.

On the whole, then, there is little evidence of spatial diffusion in legislative roll-call voting in Alþingi. With such limited evidence of peer effects, it is not possible to say much about the nature of any peer effects that may be at work but it is, nevertheless, interesting to briefly consider the results with respect to the different dependent variables. It is not surprising that the results tend to be similar when comparing the defection rates from either party or coalition (government or opposition) with the results obtained using the MPs’ estimated position on the first dimension obtained from the scaling procedures. That is, one would naturally expect the structure of party competition to be reflected in that primary cleavage (or the other way around). What is more interesting is that the evidence of peer effects is no stronger when we consider MPs’ position on the second dimension—when one might have expected the second dimension to be of secondary importance and, thus, involve issues where MPs are more easily influenced by their peers or are less constrained by party discipline. This is not the case, which suggests that the second dimension cannot be considered to be of secondary importance to the parties.¹⁹ An alternative interpretation of the absences of any substantive differences between the first and second dimensions is that there simply are no peer effects at play—even when considering issues that are less central to the parties’ policy agendas.

6.1 Robustness checks

We conducted additional analyses to further examine the consistency of our largely null findings, as it may be the case that private member bills—as opposed to government proposals—are less likely to be subjected to the effects of party discipline. Interestingly, while private member bills comprise a larger share of the proposals in Alþingi, comparatively fewer of these bills receive plenary time, with less than half subject to a vote. Perhaps of most importance here, however, is that they are largely unanimous or highly consensual. As such, they are unrepresentative of the universe of voting behavior in the parliament. Nonetheless, it is possible that coalitions on member bills leave room for some degree of peer effects given the nature of the issues involved and differing levels of political salience.

We conducted a parallel analysis—scaling the votes where possible and using the same neighbor definitions and dependent variables in a subset of sessions that saw a non-trivial number of contested votes (the 127th, 130th, 135th, 139th, and 140th)—and computed global and local Moran's I statistics and estimated spatial lag models to test for spatial dependence. Once again, we find little evidence of systematic peer effects in this smaller subsample of the legislative record, with the prevalence of statistically significant effects roughly mirroring that of the full set of votes analyzed above. Additional details on these results, along with a discussion of lopsided voting, are reported in Appendix E of the SI.

6.2 Contextualizing the results

This article aims to contribute one piece of evidence to the ongoing study of peer effects in legislatures. Indeed, the null results we find may well be confined to Alþingi. More broadly, one might suspect the effect of proximity to be weaker in systems with a high degree of party discipline. So it is important to extend research on spatial dependence in legislative politics to other parliamentary bodies. Additionally, scholars have and ought to continue to adopt varied methodological approaches to these questions. While we believe that the randomization of seating assignments in Alþingi, alongside the spatial econometric approach utilized here, offers a compelling strategy for identification that is less subject to the sorts of assumptions required when using observational data, the latter is necessary in the absence of such mechanisms. One recent example of such work is that of Harmon et al. (2019), who use variation in seating arrangement across the European Parliament's venues in Strasbourg and Brussels to identify peer effects.

And as we noted earlier, Saia (2018) also examines the effects of seating assignments in Alþingi using a very different empirical strategy to ours and finds substantial peer effects that may seem somewhat implausible given the small size of the legislature and the fact that seat assignments are randomized yearly.²⁰ Not surprisingly, the use of a different empirical strategy leads to a sharp contrast between our findings and Saia's, so it is worth clarifying how our analysis differs. Saia's main focus is whether an MP's vote diverging from her “party line,” proxied by the party leader's vote, is dependent on divergence between the party lines of neighboring MPs. Saia addresses the simultaneity problem (i.e., that MPs influence one another) by employing a two-stage least squares (2SLS) approach in which neighbors’ party lines affect their voting behavior, but do not affect legislator i's voting behavior. This exogeneity assumption inherent in an instrumental variables approach underlies Saia's empirical analyses and results. But the degree of party unity likely to occur in any legislative chamber (see, e.g., Dewan and Spirling, 2011) would mean the exclusion restriction is violated. And, as a consequence, the values on the left-hand side of the equation will influence the values on the right-hand side of the equation, producing biased parameter estimates.

In contrast, we address the simultaneity in legislative behavior more effectively via a spatial econometric modeling approach. A spatial diffusion process is consistent with a spatial lag model (a mixed regressive, spatial autoregressive model), in which the behavioral diffusion is captured via a spatial autoregressive parameter. By employing ML estimation, we are able to overcome the simultaneity problem inherent both in non-spatial models and in a 2SLS modeling approach, thereby directly accounting for the simultaneity in the Alþingi data.²¹

7. Conclusion

For many years, legislative scholars have been interested in whether legislative behavior is shaped by one's proximity to peers. This question has also informed attempts to promote comity in the US Congress, as members sought to promote bipartisanship through mixed seating at State of the Union addresses following the shooting of Representative Gabrielle Giffords (D-AZ) in 2011. The question of whether spatial proximity to other members influences legislative behavior thus carries both scholarly and practical implications.

Prior studies have often found evidence that seating location does influence voting behavior in legislatures. Members who sit together often vote together. Importantly, however, these observational studies have examined this question in legislatures in which seating assignments are not randomized. As a consequence, we cannot know whether the findings reflect peer effects—behavioral diffusion between members of the legislature—or simply homophily, as legislative birds of a feather choose to sit together.

Iceland's Alþingi provides an ideal “treatment” for examining the effects of spatial proximity on roll-call voting behavior due to the random seating lottery that occurs at the beginning of each session. This lottery allows us to set aside endogenous seating locations and examine behavioral diffusion between members. In this article, we have conducted an extensive analysis of spatial peer effects in Alþingi, employing more than 20,000 tests for spatial dependence across six measures, three neighbor definitions, and 23 sessions.

Our conclusion is simple: we find little evidence that where Icelandic parliamentarians sit influences how they vote. We uncovered only scattered evidence of spatial effects, at levels we might expect to observe by chance. Members of Alþingi generally do not influence their neighbors’ voting behavior. This finding is consistent across roll-call voting measures, across neighbor definitions, and across sessions.

Does this mean that spatial effects found in previous studies in non-randomized settings are necessarily epiphenomenal, reflective of homophily instead of behavioral influence on the floors of these legislatures? We would caution against drawing too broad a conclusion from this one case. Rather, more analysis of both the Icelandic case and other legislatures is warranted. Particularly in light of the fact that cohesion and productivity are lacking in many legislatures today, any policy proscription that might help to produce consensus deserves careful attention. And more analyses of these kinds will help to shed greater light on the reminiscences of politicians such as Robert Menendez and Joe Biden, and allow us to say with greater confidence whether they are simply anecdotal or reflective of more systematic processes occurring in legislatures. Our results also suggest that changes in seating patterns alone, such as occurred in the wake of the attempted assassination of Representative Giffords, may not significantly alter legislative behavior, at least in heavily partisan contexts. Inducing comity and cooperation in legislative bodies may require more substantial and even systemic reform efforts in legislatures and the broader political systems they inhabit.