Strategic Ambiguity of Party Positions in Multi-Party Competition

Abstract

Party competition is largely about making policy promises to voters. We argue that the clarity of the expressed policy position may be equally important. If blurred messages toward different audiences and therefore ambiguous positions can attract votes from different groups, parties have incentives to present ambiguous rather than clear-cut policy platforms. We present a formal model of multi-party competition with stochastic voting where party leaders make strategic choices on both the position and the level of ambiguity of their platforms. Leaders respond to the demands of two principals, the general public and party core constituencies. We derive two hypothesis on the location and ambiguity of party platforms and provide initial tests of these hypotheses in a comparative setting in 14 Western European democracies gathering data on voter and party left-right positions from Eurobarometer surveys and electoral manifestos. Ambiguity of party profiles is estimated using a variant of Wordscores on a newly established data set of electoral manifestos. We find that platforms become more ambiguous as the preferences of the two principals diverge. Our findings imply that ambiguity can be a winning strategy for parties, especially in settings with strong partisan lines.

When following election campaigns, both journalists and scholars frequently observe that it is impossible to precisely pin down the position of the competing parties or candidates on relevant issues. Parties and candidates often seem reluctant to say precisely what they stand for and what policies they promise to implement once they are elected into office. Such obfuscation or ambiguity is well described for the US context (Shepsle 1972; Page 1976; Bartels 1986; Aldrich 1995; Meirowitz 2005; Milita, Ryan and Simas 2014). Some even consider it a “stylized fact” about American elections that “candidates becloud their policies in a fog of ambiguity” (Downs 1957). Vagueness of party positions is also observed in multi-party systems, but when and why vagueness exists in such contexts is more complex and not well understood. In fact, most theoretical work on ambiguity focuses on two-party competition. In this study, we advance the literature on party ambiguity by presenting a formal model of multi-party competition with ambiguous party positioning. Confronting two observable implications of the model with data on 14 European party systems over 25 years provides support for our theoretical account.

It is widely accepted that ambiguity is seen as being the result of strategic behavior by parties. If targeted messages toward specific groups and therefore ambiguous positions can attract votes from different groups, parties have incentives to present ambiguous rather than clear-cut policy platforms. In fact, there is an evolving empirical literature suggesting that ambiguous policy platforms can help parties win votes (Rovny 2012; Somer-Topcu 2015).

Although the assertion that parties strategically obfuscate their programmatic positions by blurring their position is electorally rewarding seems innocent, there is less consensus on the mechanism of how ambiguity is used strategically by parties and candidates in electoral competition. In an early contribution, Shepsle (1972) finds that ambiguity is a beneficial strategy in two-candidate competition only if a majority of voters are risk-acceptant in some environment of the median voter. Under such circumstances, an incumbent (unambiguously) positioned at the median can be defeated by a challenger announcing a lottery of positions in that environment with expectation at the median. A different perspective is offered by Page (1976) and more recently by Rovny (2012), who argue that ambiguity eventually means avoiding talking about divisive issues. Candidates highlight and take a clear stance on consensus issues while blurring positions on issues where the constituency is divided to attract broader support or to not deter voters. Later works have discussed related mechanisms that result in ambiguous position taking. Some focus on the unwillingness of candidates to reveal their true position (Alesina and Cukierman 1990), either to secure flexibility in office (Aragones and Neeman 2000) or to be able to adhere to a different position after primaries reveal the preferences of the electorate (Meirowitz 2005). Further work emphasizes the uncertainty about the median voter position as possible source of candidate ambiguity (Glazer 1990) or context-dependent voting (Callander and Wilson 2008).

Although all these arguments are plausible in the context of two-party systems, little is known about whether and how they extend to or work in multi-party systems. We do not know whether and when intentional ambiguity by agents is an equilibrium strategy in a competitive environment where not one but all agents can take a clear stance or blur their position. Even less is known about the prevalence of ambiguous strategies in real-world multi-party systems beyond anecdotal or case-study evidence. The goal of this paper is precisely to answer these questions.

We present a model of multi-party competition with ambiguous position taking by parties. In line with previous works, we argue that position taking is only one aspect of strategic party competition. The clarity of the expressed position or the amount of ambiguity surrounding this position are equally important in the competition for electoral support. More specifically, we posit that in multi-party competition, party elites make strategic choices on both the position and the level of ambiguity of their platforms. Our point of departure is the more recent literature on multi-party competition that has offered a general model of elections where parties’ positional strategies are dependent not only on voters’ perception of party positions but also on the support of party activists (Schofield and Miller 2007). In the argument, originally suggested by Aldrich (1983), activists provide valuable resources to their candidate with the resources varying depending on the distance of the candidate’s position. As a result, party elites accommodate the claims of policy-motivated, non-centrist activists (see also Aldrich 1983; Strøm 1990; Ware 1992; Adams, Merrill and Grofman 2005; Adams and Somer-Topcu 2009). A related argument underlies the class of models where candidates or parties have policy preferences (Wittman 1977; Calvert 1985; Adams, Merrill and Grofman 2005) so that they adhere to divergent platforms that gear toward their core constituencies. ¹ In both arguments, the positions taken by party elites incorporate the preferences of policy-motivated activists and, for most cases, predict divergence of party positions in multi-party competition rather than convergence at the median or mean voter (Schofield and Sened 2006). This is also what we observe empirically in European multi-party systems.

The novelty of the model presented in this paper is to allow party elites to strategically choose ambiguous policy platforms in the pursuit of balancing the electoral consequences with the necessity of preserving the support of party activists. The notion of party elites who serve two competing principals, voters and party activists, is captured by the assumption that party leaders strive for both government and party office. In multi-party competition, the objective to attain government office can be proxied by the motivation to maximize vote shares in general elections. ² At the same time, party leaders strive for party office, that is, they seek to get re-elected by party members or activists in a national party conference. Of course, parties differ in the rules and practices of how they hold their leaders accountable. Party leaders may also differ in their time horizons and the compromises between the two objectives they are willing to make. What is important here is the notion that there is a set of party members or activists with the ability to displace the party leader (crystallized in the notion of the “decisive party member”).

We think of a party platform (or any other campaign message) as a piece of information that voters use to update their prior beliefs on the position of the sender of the message, the party leader. The more specific the information, the more any receiver can learn from the platform and the more similar will be the posterior beliefs of groups of voters that had different initial beliefs. An ambiguous position or platform, on the other hand, provides little information on the party leader that voters and party activists could use to update their prior beliefs. As, in the end, party leaders are also party members that have been working for and within the party for many years, we assume that the expectations or prior beliefs of party members about their leaders’ type is both more specific and biased (toward the party) than those of the general electorate. If party members differ in their policy preferences from the general electorate, leaders face a trade-off when drafting their electoral platform or manifesto (Strøm and Müller 1999). If the initial beliefs of the general electorate and party members diverge, providing an ambiguous platform can be a winning strategy. Our model suggests that formulating ambiguous policy positions can actually help leaders to do the splits.

We characterize local Nash equilibria (LNE) of the model and perform Monte Carlo simulation to derive two hypotheses on the location and ambiguity of party platforms. First, we expect that leaders draft platforms that are located between the decisive party member and the some “weighted” electoral mean. Second, leaders use more ambiguous platforms the more non-centrist the party, and hence the equilibrium platform of the party, is. Even in multi-party settings, leaders of extreme parties have incentives to get close to the electoral mean but they are pulled away by party activists. Offering an ambiguous platform can help in getting the support of regular voters and party members—even though both are risk-averse.

We provide an initial test of these hypotheses in a comparative setting in 14 Western European democracies gathering data on voter and party left-right positions from Eurobarometer surveys and political texts. ³ Ambiguity of party profiles is estimated using a variant of Wordscores (Laver, Benoit and Garry 2003) on a newly established data set of electoral manifestos. Estimating ambiguity from political texts provides a very direct measure of positional ambiguity that is not conflated with other types of (voter-based) uncertainty. ⁴ Using this novel measure of ambiguity we find evidence that ambiguous position taking is widespread and systematic across European parties. Consistent with our expectation we see that platforms become more ambiguous as the preferences of the two principals, the voting public and the party core constituency, diverge. In sum, our findings imply that ambiguity could be a winning strategy for parties, especially in settings with strong partisan lines.

This paper proceeds as follows. In the next section, we present the formal model and derive empirical expectations from a Monte Carlo simulation. We then discuss the data and the methodology used to arrive at measures of the location of party platforms, their ambiguity and the decisive party member. The third section presents results of the statistical analysis. We conclude by exploring implications of the findings for party competition and voting behavior and discussing future avenues for research.

A Model of Strategic Ambiguity

The party competition model presented here is an extension of existing models of multi-party competition that assume office-seeking parties and policy-seeking voters with proximity-based evaluation functions with stochastic components (Lin, Enelow and Dorussen 1999; Adams, Merrill and Grofman 2005; Schofield 2006). Where we differ is the assumption on parties as unitary actors. The key idea underlying our model is to distinguish party leaders from their rank-and-file. Party leaders therefore have not one but two objectives. They seek control over government office and they want to retain their party office. They benefit from party office if they get re-elected by the party rank-and-file, whereas, in multi-party competition in large districts, the government office ambition is best served when they maximize pluralities in general (Hinich and Ordeshook 1970). We therefore use the relative vote share as a reasonable proxy for the likelihood of getting into government office and assume that the goals are related in a linear, additive manner. ⁵

Assumptions

Formally, each party leader j is characterized by an objective function that maximizes a linear combination of the expected utilities from getting elected into government and party office (where the utilities for getting elected and not getting into government and party office are normalized to 1 and 0):

(1) $$u_{j} \,({\hat {\bf z}}})\,{\equals}\,p_{{1j}} {\plus}\alpha p_{{2j}} .$$

The probability p _1j is the expected vote share of party j, p _2j the probability that the party leader stays in party office, α>0 a weighing parameter that we assume to be constant across parties.

We assume a set of voters N={1, … , n} with generic voter i having a canonical quadratic random utility function with ideal point $$\it x_{i} \in X$$ where X is a closed interval in $${\Bbb R}$$ . There is a set of P parties. Any party j has a pivotal party member with ideal point $$x_{{m_{j} }} $$ (and quadratic random utility functions) who has the decisive vote on the party convention or similarly that selects the party leadership. Party leaders choose a policy platform to declare $$\hat{z}_{j} $$ . We depart from previous work on party competition by allowing party leaders to present an ambiguous party platform rather than a single, unique policy position to their constituencies. We think of a platform as a random variable that is realized after the election. To keep things as simple as possible, we assume that the platform $$\hat{z}_{j} $$ has a uniform distribution on the interval $$\left[ {z_{j} {\minus}\sqrt 3 \sigma _{j} ,\,z_{j} {\plus}\sqrt 3 \sigma _{j} } \right]$$ . The strategy of a party leader thus involves choosing a platform mean z _j and a platform variance $$\sigma _{j}^{2} $$ rather than a single and unambiguous point. Let $${\hat {\bf z}}} \,{\equals}\,(\hat{z}_{1} ,\,\ldots\!,\hat{z}_{P} )$$ be a generic vector of these party platforms.

As noted above, we assume that voters have quite unspecific expectations and evaluate party platforms where they are likely given the information they receive. We can think of voters with uninformative, uniformly distributed priors on X that are updated via Bayes’ rule using the information $$\hat{z}_{j} $$ so that their posterior belief about the party position is just $$\hat{z}_{j} $$ . Therefore, each voter is described by the vector of expected utilities $$v_{i} (\hat {\bf z} ){\equals}(v_{{i1}} (\hat{z}_{1} ),\,\ldots\!,v_{{ip}} (\hat{z}_{p} ))$$ where, for the density f _j of the uniform distribution $$U\left( {z_{j} {\minus}\sqrt 3 \sigma _{j} ,\,z_{j} {\plus}\sqrt 3 \sigma _{j} } \right)$$

$$v_{{ij}} (\hat{z}_{j} ){\equals}{\int} {({\minus}(x_{i} {\minus}y)^{2} {\plus}{\epsilon}_{j} )f_{j} (y)\:dy\,{\equals}\,{\minus}\sigma _{j}^{2} {\minus}(x_{i} {\minus}z_{j} )^{2} {\plus}{\epsilon}_{j} .} $$

The first term, $$v_{{ij}}^{{\asterisk}} (\hat{z}_{j} ){\equals}{\minus}\sigma _{j}^{2} {\minus}(x_{i} {\minus}z_{j} )^{2} $$ , is the observable part of the utility that decreases in the distance between the voter ideal point and the expected party position. As voters are risk-averse, utility is decreasing whenever the variance of the platform increases. The second term, ε _j , is the stochastic component of the utility function. Following previous work on stochastic voting models, we assume that any ε _j has a type I extreme value distribution. With this assumption, the probability that voter i votes for party j is given by

$$\rho _{{ij}} ({{\hat {\bf z}}} ){\equals}{{{\rm exp}[v_{{ij}}^{{\asterisk}} (x_{i} ,\,\hat{z}_{j} )]} \over {\mathop{\sum}\limits_{k{\equals}1}^P {\rm exp}[v_{{ik}}^{{\asterisk}} (x_{i} ,\,\hat{z}_{k} )]}}.$$

The expected vote share of party j is $$p_{{1j}} ({{\hat {\bf z}}} ){\equals}{1 \over n}\mathop{\sum}\limits_{i{\equals}1}^n \rho _{{ij}} ({{\hat {\bf z}}} )$$ and the marginal changes in the expected vote share are given by

(2) $$\eqalign{& {{{\partial p_{{1j}} } \over {\partial z_{j} }}} \,{{\equals}{1 \over n}\mathop{\sum}\limits_{i{\equals}1}^n 2(x_{i} {\minus}z_{j} )(\rho _{{ij}} {\minus}\rho _{{ij}}^{2} ),} \hfill \cr & {{{\partial p_{{1j}} } \over {\partial \sigma _{j} }}} \,{{\equals}{1 \over n}\mathop{\sum}\limits_{i{\equals}1}^n {\minus}2\sigma _{j} (\rho _{{ij}} {\minus}\rho _{{ij}}^{2} ).} \hfill \cr } $$

We point to three noteworthy implications: first, the first derivative is positive whenever z _j is smaller than what we henceforth refer to as the “weighted electoral mean” of party j (Schofield 2007):

(3) $$EM_{j} \,{\equals}{{\mathop{\sum} (\rho _{{ij}} {\minus}\rho _{{ij}}^{2} )x_{i} } \over {\mathop{\sum} (\rho _{{ij}} {\minus}\rho _{{ij}}^{2} )}}.$$

Thus, the electoral support of a party increases when the platform mean moves toward the weighted electoral mean. We should emphasize that unlike the conventional “electoral mean”, $${1 \over n}\mathop{\sum} x_{i} $$ , EM _j is specific to each party and varies with the platform profile $${{\hat {\bf z}}} $$ as all the ρ _ij are functions of $${{\hat {\bf z}}} $$ . Whatsoever, the weighted electoral mean represents the electoral pull on the party, that is, the direction where additional votes can be gained. Second, the derivative of the vote share with respect to the platform variance is strictly negative, which is a straightforward implication of the assumption that voters are risk-averse. Third, if party leaders were concerned about winning government office, only, that is α=0, the unique Nash equilibrium would be the strategy profile where each party leader would present an unambiguous, zero-variance platform at the mean voter position. This is the stochastic mean voter theorem (Lin, Enelow and Dorussen 1999) for a one-dimensional policy space.

As we argued above, party members certainly have more specific expectations on where their party leaders stand as compared with the more diffuse expectations of non-party members. Still, party members may be prepared to accept policy compromises of their leaders as a means to attain government office. They will thus use the information that is contained in the platform to update their beliefs about likely policies the party leader will pursue once she is elected into government. We can think of the prior expectation of the decisive party member as a random variable which we assume to be, to make things as simple as possible again, uniformly distributed over $$[x_{{m_{j} }} {\minus}\sqrt 3 \omega ,\,x_{{m_{j} }} {\plus}\sqrt 3 \omega ]$$ where $$x_{{m_{j} }} $$ is the position of the decisive party member (aka the median party member) and ω is the variance of the prior. ⁶

Updating a uniform prior distribution (the initial belief) with uniformly distributed new information (the platform) is straightforward. As long as party leaders are interested in both government and party office, the support intervals will intersect and the posterior simply is a uniformly distributed random variable over the intersection of the two supports. As we know that in any equilibrium, the platform mean of any party is located between the weighted electoral mean and the decisive party member (see Proposition in the supplementary material), the posterior belief of the decisive party member m _j is given by

$$\eqalignno{ & U(x_{{m_{j} }} {\minus}\sqrt 3 \omega ,\,z_{j} {\plus}\sqrt 3 \sigma _{j} )\quad {\rm if}\;EM_{j} \leq z_{j} , \cr & U(z_{j} {\minus}\sqrt 3 \sigma ,\,x_{{m_{j} }} {\plus}\sqrt 3 \omega )\quad {\rm if}\;z_{j} \,\lt\,EM_{j} . $$

These posterior distributions have means $$\mu _{j} {\equals}{1 \over 2}(z_{j} {\plus}x_{{m_{j} }} \,\pm\,\sqrt 3 (s{\minus}t))$$ and variances $$\tau _{j} {\equals}{{\sigma {\plus}\omega } \over 2}\,\pm\,{{z_{j} {\minus}x_{{m_{j} }} } \over {2\sqrt 3 }}$$ where ± refers to the two cases EM _j ≶x _mj . The decisive party member’s expected utility of the party leader then simply is $$v'_{j} (\mu _{j} ,\,\tau _{j} ){\equals}{\minus}\tau _{j}^{2} {\minus}(x_{{m_{j} }} {\minus}\mu _{j} )^{2} {\plus}{\epsilon}_{j} $$ .

How likely is it that a party leader proposing a platform that does not perfectly match the prior expectations of her party constituency actually gets re-elected? Although we do not know the exact offer or promise of the party leader’s intra-party challenger to the rank-and-file, assuming that the decisive party member’s evaluation of the challenger is given by some exogenous $$v_{j}^{c} {\plus}{\epsilon}_{j}^{c} $$ , the re-appointment probability of the party leader is given by $$p_{{2j}} {\equals}{{{\rm exp}[v'_{j}{^{\asterisk}} ]} \over {{\rm exp}[v'_{j}{^{\asterisk}} ]{\plus}{\rm exp}[v_{j}^{c} ]}}$$ . The marginal changes (and that is what we are really interested in) then are

(4) $$\eqalign{ &{{{\partial p_{{2j}} } \over {\partial z_{j} }}} \,{{\equals}{1 \over 3}(\,\mp\,2\sqrt 3 \sigma _{j} \,\pm\,\sqrt 3 \omega {\plus}2(x_{{m_{j} }} {\minus}z_{j} ))(p_{{2j}} {\minus}p_{{2j}}^{2} ),} \hfill \cr& {{{\partial p_{{2j}} } \over {\partial \sigma _{j} }}} \, {{\equals}\left( {{\minus}2\sigma _{j} {\plus}\omega \,\pm\,{{2(x_{{m_{j} }} {\minus}z_{j} )} \over {\sqrt 3 }}} \right)(p_{{2j}} {\minus}p_{{2j}}^{2} ),} \hfill \cr } $$

where we again save notation and write ± for the cases EM _j ≶x _mj .

Equilibria

At a Nash equilibrium of the model, the partial derivatives of u _j , the party leaders’ utility function, with respect to z _j and σ _j are 0 for all P parties. That is

(5) $$\eqalign{ {{{\partial u_{j} } \over {\partial z_{j} }}} \,{{\equals}{{\partial p_{{1j}} } \over {\partial z_{j} }}{\plus}\alpha {{\partial p_{{2j}} } \over {\partial z_{j} }}{\equals}\,0,} \hfill \cr {{{\partial u_{j} } \over {\partial \sigma _{j} }}} \,{{\equals}{{\partial p_{{1j}} } \over {\partial \sigma _{j} }}{\plus}\alpha {{\partial p_{{2j}} } \over {\partial \sigma _{j} }}{\equals}\,0.} \hfill \cr } $$

Substituting the above equation for Equations 2 and 4, and solving for z _j and σ _j gives for all j:

(6) $$\eqalignno{ & z_{j} \,{\equals}\,{{3\mathop{\sum} (\rho _{{ij}} {\minus}\rho _{{ij}}^{2} )x_{i} {\plus}\alpha n(p_{{2j}} {\minus}p_{{2j}}^{2} )\,\left( {x_{{m_{j} }} \,\mp\,\sqrt 3 \sigma _{j} \,\pm\,{1 \over 2}\sqrt 3 \omega } \right)} \over {3\mathop{\sum} (\rho _{{ij}} {\minus}\rho _{{ij}}^{2} ){\plus}\alpha n(p_{{2j}} {\minus}p_{{2j}}^{2} )}}, \cr & \sigma _{j} \,{\equals}\,{{\alpha n(p_{{2j}} {\minus}p_{{2j}}^{2} )\,\left( {\,\pm\,{1 \over {\sqrt 3 }}(x_{{m_{j} }} {\minus}z_{j} ){\plus}{1 \over 2}\omega } \right)} \over {\mathop{\sum} (\rho _{{ij}} {\minus}\rho _{{ij}}^{2} ){\plus}\alpha n(p_{{2j}} {\minus}p_{{2j}}^{2} )}}. $$

Unfortunately, there is no simple closed-form solution to these equations as all probabilities, the ρ’s and p’s, are also functions of z and σ .

So what can we learn from these equations? We note that the additive “probability” terms in both denominators (the “ $$(\rho _{{ij}} {\minus}\rho _{{ij}}^{2} )$$ ”, the “ $$\alpha n(p_{{2j}} {\minus}p_{{2j}}^{2} )$$ ” and the “ $$\alpha n(p_{{2j}} {\minus}p_{{2j}}^{2} )$$ ” terms) also show up in the nominators suggesting that they serve as some sort of weight for the constitutive, “distance” terms in the nominators. To get a better intuition, we substitute Equation 6 for the definition of the weighted electoral mean, EM _j , from Equation 3 and use the definition $$\lambda {\equals}{{\mathop{\sum} (\rho _{{ij}} {\minus}\rho _{{ij}}^{2} )} \over {\alpha n(p_{{2j}} {\minus}p_{{2j}}^{2} )}}$$ . We can then rewrite Equation 6 as follows:

(7) $$\eqalign{& {z_{j} } \, {{\equals}{{3\lambda EM_{j} {\plus}(x_{{m_{j} }} \,\mp\,\sqrt 3 \sigma _{j} \,\pm\,{1 \over 2}\sqrt 3 \omega )} \over {3\lambda {\plus}1}},} \hfill \cr& {\sqrt 3 \sigma _{j} } \, {{\equals}{{\,\pm\,(x_{{m_{j} }} {\minus}z_{j} ){\plus}{1 \over 2}\sqrt 3 \omega } \over {\lambda {\plus}1}},} \hfill \cr } $$

which gives a more sensible idea of the equilibrium strategies. The first equation suggests that party leaders propose platforms, the means of which are weighted averages of EM _j and $$x_{{m_{j} }} \,\mp\,\sqrt 3 \sigma _{j} \,\pm\,{1 \over 2}\sqrt 3 \omega $$ . In other words, the platform means balance the pull of the general electorate and that of the party members. The weights of the convex combination are just 3λ/(3λ+1) and 1/(3λ+1). The second equation suggests that, in the same vein, the level of ambiguity of the platform (note that $$\sqrt 3 \sigma _{j} $$ is just half the length of the platform) is a convex combination of 0 and $$\,\pm\,(x_{{m_{j} }} {\minus}z_{j} ){\plus}{1 \over 2}\sqrt 3 \omega $$ . The weights here are λ/(λ+1) and 1/(λ+1).

Put simply, while we know what the equilibrium looks like—the platform mean is a convex combination of the weighted electoral mean and the party activist position—there is no way to write down the equilibrium in plain numbers as the weighted electoral mean, EM _j , is itself a function of the individual voting probabilities ρ _ij —that is, it is an endogenous variable. Thus, the recursive nature of the above equations precludes making straightforward and simple statements on the expected location of the party leaders’ platforms. However, we establish conditions for the existence and uniqueness of LNE, which we provide in a theorem in the supplementary material. Moreover, we can use Monte Carlo techniques to numerically simulate the equilibrium model which will provide us with testable hypotheses about the nature of party competition with ambiguous messages. This is what we do next.

Monte Carlo Simulation

We set up a Monte Carlo simulation to come up with expectations on party platforms in equilibrium. In particular, we shall see that platform variances are ceteris paribus larger the more distant the equilibrium mean position is from the weighted electoral mean of the party. To this end, we implement an iterative approximation algorithm using the λ contraction T from the Theorem in the supplementary material. While we neither know the number of LNE nor the size of the environment U where unique local equilibria exist, contraction T guarantees that the iterative approximation algorithm converges to an LNE in the environment of the starting point. ⁷

More specifically, we run a series of 100 scenarios. In any of these scenarios, the ideal points x _i ’s of 1000 voters are sampled from a normal distribution with mean 0 and unit variance, a party system with $$P\in\{ 3,5,7\} $$ parties (size of the party system sampled from a uniform distribution) is set up with positions of decisive party members, $$x_{{m_{j} }} $$ , also sampled from N(0, 1). For each scenario, the approximation algorithm was set up with ten different starting values where values for the z _j ’s were sampled from $$U(0,\,x_{{m_{j} }} )$$ and starting values for σ _j ’s are drawn from a uniform distribution over the interval from 0 to $$\,\mid \!x_{{m_{j} }} {\minus}{\rm starting}\;{\rm value}(z_{j} )\!\mid\!\!\,/\,\sqrt 3 {\plus}{1 \over 2}\omega $$ . We fix ω to 0.2. With this initial setup unique LNE exist in all 100 scenarios.

The results for four exemplary scenarios are shown in Figure 1. We point out three notable observations. First, the mean of any equilibrium platform (z _j , represented by a star) is located between the decisive party member ( $$x_{{m_{j} }} $$ , filled circle) and the party’s weighted electoral mean (EM _j , hollow circle), which follows from what we found above. Second, the panels suggest that platform ambiguity (σ _j ) is a function of the spatial location of the platform mean and/or the party’s weighted electoral mean. When the decisive party member is close to the weighted electoral mean and/or close to the mean of the voter distribution, the equilibrium platform is less ambiguous. Parties at the extremes of the party system, in particular when the distance between decisive party member and electoral mean is large, present more ambiguous party platforms in equilibrium. Third, we note that the party’s weighted electoral means—which represent the electoral pull on the party leaders—are centrally located.

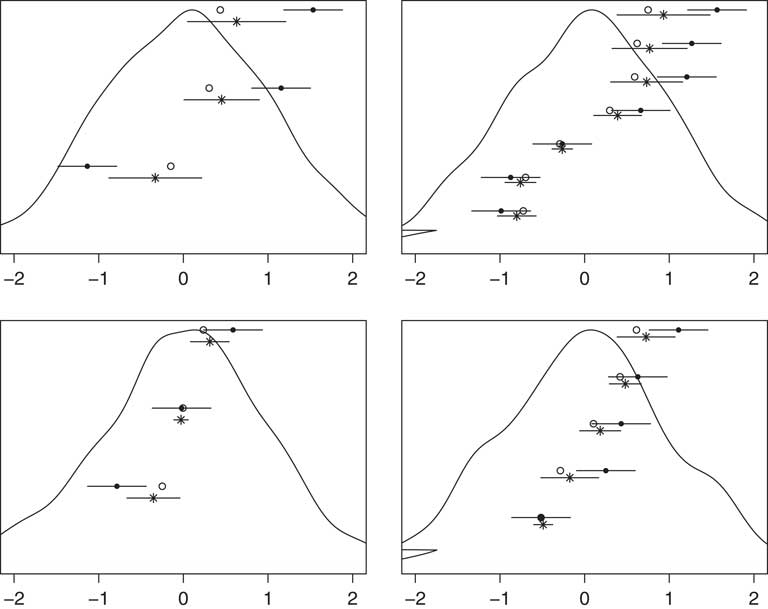
Fig. 1 Monte Carlo simulation of ambiguity model of party competition Note: Numerical equilibria of four exemplary runs of the model described in the main text (with n=1000 voter ideal points sampled from N(0, 1), and decisive party members $x_{{m_{j} }} $ sampled from N(0, 1)). Panels show voter distribution as well as, for each party, the prior belief of the decisive party member $[x_{{m_{j} }} {\minus}{1 \over 5}\sqrt 3 ,\,x_{{m_{j} }} {\plus}{1 \over 5}\sqrt 3 ]$ (interval with filled circle), the weighted electoral mean EM _j (hollow circle) and the party equilibrium platform $[z_{j} {\minus}\sqrt 3 \sigma ,\,z_{j} {\plus}\sqrt 3 \sigma ]$ (interval with star).

Finally, we run a series of regressions for the 100 scenarios and find that the level of ambiguity is linearly related to the distance between the weighted electoral mean and the platform mean. Although this provides us with a quite specific hypothesis (“the level ambiguity of a party platform increases in $$\,\mid\!EM_{j} {\minus}x_{{m_{j} }} \!\mid\,$$ ”), there is no way to test it in such a specific way as the weighted electoral mean is an unobservable variable.

We therefore seek to provide an initial test of our theory of ambiguous platforms by testing two weaker hypotheses. Although we do not know the exact location of the weighted electoral mean EM _j and therefore cannot derive hypotheses directly, the simulation results suggest that the EM _j ’s are more centrist than the decisive party members, in many cases they are even close to the (unweighted) electoral mean (which is close to 0 in the simulation panels of Figure 1). This provides two hypotheses on party competition in a world with ambiguous party platforms. As the model considers a world where party leaders can choose both a ideological position (or platform mean) and a level of ambiguity, the first concerns the location of party platform means whereas the second refers to platform ambiguity:

HYPOTHESIS 1: The mean of the platform of a party is more centrally located than the position of the decisive member of that party.

HYPOTHESIS 2: The relationship between party platform means and party platforms variances is U-shaped, that is, platform variances are smaller the more centrally located the platform means.

We now seek to test these expectations with real-world data.

Data and Measurement

To test our expectations, we need a measure of platform ambiguity, or, more generally, the heterogeneity of positions taken by or within a party. The literature offers several ways to arrive at such a measure. Let us quickly outline what these alternatives are before we elaborate in more details on the method chosen for the empirical analysis of party systems in 14 countries in this paper. One option to measure intra-party heterogeneity—which has been used most extensively in the literature—is to look at roll-call votes (e.g., Sieberer 2006; Ensley 2011; Tavits 2011). There are at least two reasons why measures of diversity based on roll-call votes are problematic for the purpose of our study. First, roll-call votes may properly reflect the cohesion of MPs’ preferences but they may also suppress existing heterogeneity in the presence of disciplinary measures by the party leadership or anticipated negative consequences of dissenting behavior such as career concerns of individual MPs or the loss of government office (e.g., Ceron 2012). This is particularly relevant in parliamentary democracies. Given that roll calls are hardly random samples of the total of votes called (Carrubba, Gabel and Hug 2008), any intra-party heterogeneity measure based on roll-call votes is likely to be downward biased. Second, our argument focuses on the electoral arena. Our model links promises made by the party leadership to the preferences of voters and of the party rank-and-file—we make no presumptions as to how electoral promises map into actual party behavior.

A second option to derive measures of party policy ambiguity is to make use of expert surveys (e.g., Rovny 2012; Greene and Haber 2015). Here, experts are either asked directly after their perceived level of dissent within parties or heterogeneity is proxied by the variation in party policy positions perceived by the experts. The latter obviously is a rough proxy, only. Variation in perceived positions of a party may indicate intra-party heterogeneity when experts refer to different party factions with different views. They may also reflect the uncertainty in the point estimate when experts simply have no clue as to what the true position of a (minor) political party is. As with most expert surveys, a drawback of the approach is that we have infrequent observations over time. This makes the use of this type of data infeasible if we are interested in examining processes and trends over time. ⁸

Other scholars have constructed measures of ambiguity from electoral survey data where either indirect measures of uncertainty of candidate positions have been derived from patterns of “don’t know” responses or the variation in perceived party placements across all respondents (Campbell 1983; Bartels 1986; Gill 2005). As pointed out by Bartels (1986) and Tomz and van Houweling (2009), there is no straightforward connection between individual-level uncertainty and population-wide variability of political positions. A wide distribution of perceptions of policy positions does not equal an ambiguous position, as even if all voters were uncertain about a candidate’s position but had exactly the same (biased) expectation, standard deviations or entropy scores would overestimate the certainty of the candidate or party position. Even more relevant in our context is the fact that voter’s uncertainty about a party position is only indirectly connected to the ambiguity of party positions as announced by the parties. Uncertainty arises not only when candidates or parties make ambiguous statements, but also when voters fail to receive the message, interpret it wrongly or are apathetic toward the political statement. So, while perceptual voter data are useful for exploring electoral consequences of uncertainty in party positions (see e.g., Dahlberg 2009; Somer-Topcu 2015), our argument focuses on strategic positioning of parties and for this purpose perceptual measures of party positions are of little use.

We choose a different approach and rely on information derived from political text to generate a measure of platform ambiguity. ⁹ Electoral manifestos are specifically drafted for the public but contain original, undistorted communication by the party itself. This makes this type of document of special value to measure not only party positions but also party platform variance. We acknowledge that our measure has limitations as well. First, we cannot capture ambiguity in policy positions if a party decides to remain silent on the topic instead of issuing a position (for a discussion of various ambiguity strategies, see Milita, Ryan and Simas 2014; Somer-Topcu 2015). Although this might pose a serious problem if one were interested in a single issue, it is less relevant here as we measure positions and ambiguity at the aggregate level of a left-right ideological scale. Parties cannot afford to be silent on all issues. Second, we may underestimate ambiguity to the extent that party elites appeal to different groups with “mixed signals”, for instance, by drafting a leftist manifesto to please party activists but communicating more liberal positions to business leaders. In sum, these deficiencies do not weight out the central advantage of our measure, namely to capture direct communication by political parties.

Recently, much work have used election manifestos to estimate party positions in spatial models using automated text analysis (Laver, Benoit and Garry 2003; Monroe and Schrodt 2008; Slapin and Proksch 2008; Quinn et al. 2010; Lowe et al. 2011). An advantage of utilizing election manifestos is that data are—more or less—readily available and allow to trace party positions over a longer period of time. A large range of election manifestos is accessible through the open access archive (www.polidoc.net) where more than 1000 manifestos from 18 countries between 1980 and today are available (Benoit, Bräuninger and Debus 2009). We use data for Austria, Belgium, Denmark, Finland, France, Germany, Ireland, Italy, Luxembourg, the Netherlands, Portugal, Spain and the United Kingdom. In the empirical analysis, we have 59 single party-systems-in-an-election-year with a total of 321 parties. A list of these parties is shown in the supplementary material for this article.

We use an automated text analysis approach that allows us to estimate policy-specific party positions as well as a measure of the ambiguity of these policy positions over time and for a wide range of countries. ¹⁰ More specifically, we build on the Wordscores approach (Laver, Benoit and Garry 2003; Lowe 2008). The basic idea of this technique is to compare the frequency distribution of words from different texts and to estimate the policy-area-specific position of a text on the basis of the differences in the share of used words within a given set of political documents. Wordscores compares the relative word frequency of a text whose programmatic position is known to the word distribution of a text of the same character whose position is unknown. Laver, Benoit and Garry (2003, 314–5) refer to these two types of documents as “reference texts” and “virgin texts”, respectively.

The key assumption behind Wordscores is that political actors do not use words randomly. Instead, to send “ideological signals” (Pappi and Shikano 2004) in their election manifestos parties will use some words more often and others less often or even never. The intuition behind the Wordscores approach then is the following: every word in a political text indicates a position on a given scale. The average position of all words in a text thus marks the position of the party. Given this setup, we argue, the dispersion of the positions of individual words has a straightforward interpretation. It carries information about positions taken within the party platform. If, for instance, a text simultaneously contains “rightist” words, that is words associated with a right-wing ideology, but also “leftist” words, that is words used signaling a left ideology, this pattern can be interpreted as an ambiguous position taking. This is exactly what we do here. ¹¹ Formally, suppose that w is the vector of relative word frequencies of an election manifesto (virgin text) in the k-dimensional universe of all reference text words and ξ is the vector of word positions (the “Wordscores” from the reference texts). We then use the standard deviation of the word positions as a measure for the level of positional ambiguity:

$$\sigma _{\xi } \,{\equals}\,\sqrt {\mathop{\sum}\limits_{i{\equals}1}^k w_{i} (\xi _{i} {\minus}\mu )^{2} } $$

where $$\mu \,{\equals}\mathop{\sum} w_{i} \xi _{i} $$ is the position (or textscore) of the manifesto. Note that σ _ξ is different from what Laver, Benoit and Garry (2003) refer to as the standard error of the position estimate, or $$\sigma _{\xi } \,/\,\sqrt N $$ (N is the number of scored words). The standard error reflects the uncertainty associated with the estimate of the (mean) text position, whereas the standard deviation reflects the diversity of positions within the manifesto. In terms of our model, we identify the platform mean by μ and the platform variance by $$\sigma _{\xi }^{2} $$ .

It is worth emphasizing that the selection of the set of reference texts is probably the most crucial decision taken by the researcher in this type of analysis (Laver, Benoit and Garry 2003). When the texts to be analyzed are manifestos, the most natural candidates for reference texts are other manifestos that address similar issues. These documents are similar in terms of the structure of the text, syntax, terminology and the set of words used. For the purpose of this paper, we use election manifestos of the year 2002, the last year in our sample, as reference text (2001 or 2003 depending on the election timing in the countries under study). ¹² Reference scores are taken from the Comparative Manifesto Project (CMP) (Budge et al. 2001; Klingemann et al. 2006). For the analyses, we have rescaled the CMP positions on the left-right (“RILE”) dimension from the −100 to +100 scale used by CMP to the 1–10 scale that is customarily used in survey research.

To summarize, we estimate the two key variables of interest from party manifestos using the Wordscores method. The first variable is the mean position of the electoral platform of a political party on the left-right scale, the second variable is the ambiguity of the platform that we operationalize by the dispersion of Wordscores in a given text. Among those parties with the largest ambiguity in our sample are the Conservative People’s Party in Denmark, the Centre Union in Italy in 1996, whereas those with the lowest ambiguity scores are the Italian Green Federation in 1992 and the Finnish Centre Party in 1995. Figure 2 provides a first glance into the possible relationship between party platform means and platform ambiguity. ¹³ As the scatterplot implies, ambiguity is on average larger, the more extreme party platforms are.

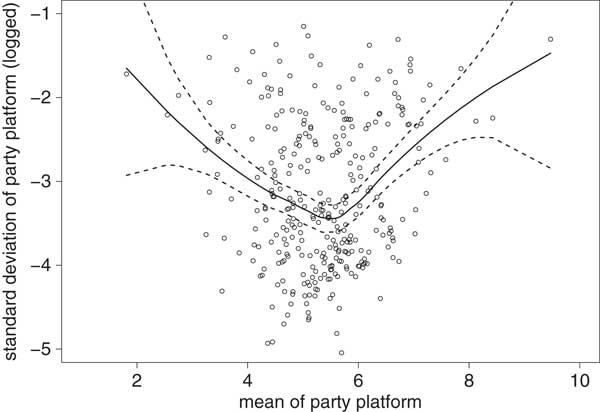
Fig. 2 Scatterplot of party platform means and party platform ambiguity for 321 parties in 59 party system-elections Note: The solid line shows the Loess curve, fitted with smoothing parameter α=0.7 and a polynomial degree of λ=2. The dotted lines show the limits of the 95 percent confidence band.

To test our theoretical expectations, data on the voter distribution are derived from the Eurobarometer surveys that provide information on ~1000 individuals in each member state of the European Union at one point in time (Schmitt and Scholz 2005). One of the survey questions asks the respondents to place themselves on a 1–10 left-right ideological scale. To test our first hypothesis, we need to know the spatial location of the party activists or the decisive party member. The proxy that we use is the conventional mean of the self-placements of the party supporters for each party in a given year. In detail, we rely on the vote intention in combination with the left-right self-placement question. The position of the decisive party member is calculated as the mean left-right self-placement for all respondents who indicated that they would support the party in the upcoming parliamentary elections (see also Ezrow et al. 2011). We should stress that this measure is a proxy only, as we do not have reliable information on the exact position of active party members. In fact, the Eurobarometer survey does not include such information and there is no other cross-national source that captures party member positions over time.

As a consequence of the standardization used by Wordscores, the estimated party position are on (roughly) the same 1–10 scale as the reference scores. Voter and party measures thus refer to the same left-right dimension and are on a similar 1–10 scale which allows for meaningful comparisons of voter and party positions and ambiguities.

A multivariate, multilevel linear regression model is specified to test the second hypothesis. To account for heterogeneity across national party systems and variation over time, we specify a two-level mixed model with the higher level being the national party system at a point in time. ¹⁴ We allow the slopes of the coefficients to vary according to this context and also these random effects to be correlated (which is of particular importance when specifying quadratic terms, see Gelman and Hill 2007): more specifically, our model reads as follows:

$$\eqalignno{ & {\rm log}(\sigma _{{\xi ,\,ij}} )\,{\equals}\,\beta _{{0j}} {\plus}\beta _{{1ij}} z_{{ij}} {\plus}\beta _{{2ij}} z_{{ij}}^{2} {\plus}{\bf{X}} _{{ij}} {\mib{\beta }} _{{3ij}} {\plus}{\epsilon}_{{ij}} , \cr & \beta _{{0j}} \,{\equals}\,\gamma _{0} {\plus}\delta _{{0ij}} ,\;\beta _{{1ij}} \,{\equals}\,\gamma _{1} {\plus}\delta _{{1ij}} ,\;\beta _{{2ij}} \,{\equals}\,\gamma _{2} {\plus}\delta _{{2ij}} , \cr & (\delta _{{0ij}} ,\,\delta _{{1ij}} ,\,\delta _{{2ij}} )\,\sim\,N_{3} (0,\,{\bf \Psi }),\;{\epsilon}_{{ij}} \,\sim\,N(0,\,\sigma _{e}^{2} ), $$

where σ _ij and z _ij are the platform standard deviation and the platform mean of party-at-election-time i in country j. The δ _j is the random-effect coefficient for country j with covariance matrix Ψ assumed to be constant across countries. The statistical model also includes a series of controls, X. A first control refers to characteristics of the election program. Election manifestos differ widely in length and as the size of the vocabulary used in a text may vary with the length of the text, the variance of the ideological signals send by these words may be smaller in shorter texts. We therefore add a control for the length of the program. Initial analyses suggest that the largest proportion of variance in the dependent variable in the models presented below is captured by the log of the inverse of the number of words used in a manifesto. We refer to this as the wordcount. A second set of controls refers to the relative position of a party in the party system of a country. More specifically, we control for the size of a party to reflect the relative weight of a party in party competition. Party size is the vote share a party received in the national election at the point in time under question. Second, the recent literature has put a lot of emphasis on a presumably different logic of party competition for niche and mainstream parties (e.g., Meguid 2005; Adams et al. 2006; Ezrow et al. 2011). We therefore add an identifier for niche party status. ¹⁵ Government party indicates whether the party has been in government or in opposition at the time the party manifesto had been drafted. In addition, we add a control for the available space around a party (distance to the closest next party) to account for the fact that with little space available, parties could become less ambiguous.

Empirical Results

We consider party manifestos as bundles of ideological signals that are directed toward at least two audiences, the general electorate and the party activists. Both groups differ in their stance or position on specific policy issues and thus party elites that seek both government participation and party leadership will seek to send targeted messages to either. Although each audience may also be targeted via specific communication channels, party manifestos summarize these diverse ideological signals resulting in more or less clear-cut political statements. In multi-party competition, when parties represent constituencies with distinct interests, party leaders may have different incentives to be ambiguous. This is what our theoretical model predicts.

We found that in equilibrium, party platform means (z _j ) are located between the weighted electoral mean of the party (EM _j ) and the decisive party member ( $$x_{{m_{j} }} $$ ). On the empirical front, while we have a reasonable proxy for the position of party members, the location of the weighted electoral mean of the party is not readily measurable. Recall that EM _j is the weighted mean voter position where the weights are determined by the probabilities with which individuals cast votes for each party (see Equation 3). We simply do not have sufficient information on individual voting behavior in our data to estimate these probabilities. We know, however, that the weighted electoral mean is centrally located. For this reason, in equilibrium, the platform mean will be more centrally located than the decisive party member. This is our first hypothesis.

To test this expectation we run a simple linear regression analysis of the party platform means on the positions of the decisive party members. As the argument refers to all parties of one specific party system in a given year and country, we set up a regression model with varying slopes and intercepts. As an initial step we center both variables at the position of the unweighted mean voter in each party system-election which gives us a rough proxy of the center of the space. The expectation then is that the regression coefficient for the position of the decisive party member is smaller than 1 while the intercept is close to 0. We find strong supporting evidence for Hypothesis 1. As Table 1 shows the average slope or “fixed effect” is as small as 0.319 with a small variance of 0.032 of the random effect.

Table 1 The Effect of the Position of the Decisive Party Member ( $$x_{{m_{j} }} $$ ) on the Mean of the Party Platform (z _j )

Note: Estimates and standard errors for parameters of a multilevel model that includes party system-election varying intercepts and slopes.

***p<0.001, **p<0.05, *p<0.1 (two-tailed).

The formal model also provides us with a second hypothesis on the strategic choice of party platform ambiguity. Based on the findings of the Monte Carlo simulation, we expect that the relationship between party platform means and party platform variances is U-shaped (Hypothesis 2), that is, parties in the “middle” of the party system ceteris paribus have more distinct positions than parties more at the extremes of the party system.

In Table 2, we report estimates for three models to test the second hypothesis. The three models differ in the complexity of the covariates considered. In column 1, we present estimates for a basic model specification that includes the party position, the squared party position and the wordcount control. Column 2 reports estimates for a model that includes the same covariates plus further controls for the status of the party in the party system. Column 3 tests for some further covariates which slightly reduces the number of observations. The upper part of the table reports fixed effects, the lower the various random terms.

Table 2 The Effect of the Platform Mean on the Ambiguity of the Platform

Note: The dependent variable is $${\rm log}(\sigma _{\xi } )$$ . Estimates and standard errors for parameters of multilevel models that include party system-election varying intercepts and slopes.

***p<0.01, **p<0.05, *p<0.1 (two-tailed).

Overall, the results indicate that the relationship between platform means and platform ambiguities is U-shaped. Although the quadratic term is positive and significant, it is a weak criterion as the relationship might be convex but monotone over the range of relevant platform means (Lind and Mehlum 2010). Rather a U-shape is implied by the condition $$\beta _{1} {\plus}2\beta _{2} x_{l} \,\lt\,0\,\lt\,\beta _{1} {\plus}2\beta _{2} x_{r} $$ for a reasonable interval $$[x_{l} ,\,x_{r} ]$$ of platform means. We adopt a conservative approach and test the combined null hypothesis that either $$\beta _{1} {\plus}2\beta _{2} x_{l} \geq 0$$ or $$\beta _{1} {\plus}2\beta _{2} x_{r} \leq 0$$ for the interquartile range of platform means (4.7, 5.9) of the entire sample. The slopes are −0.033, 0.032 and −0.032 and the null hypothesis can be rejected with p=0.002. In other words, there is strong evidence that the relationship between platform means and platform ambiguity is U-shaped in the empirical range of platform means.

Although most controls have a significant influence on our dependent variable, they do not weaken the theoretically interesting relationship between party positions and their ambiguity, the results remain stable. The random terms show considerable variation between the party system-elections, not only in terms of intercepts (Var(Constant)) but also in terms of the strength of the U-shape. The control variables perform as expected if they reach significance at all. Longer manifestos are in tendency less ambiguous and parties in government draft slightly more precise manifestos than opposition parties. One might argue that what government parties promise is more rooted in reality or more constraint by the status quo than what the opposition proposes. We also find that election manifestos of niche parties are slightly more ambiguous than those of mainstream parties—a finding that reflects the different nature of party competition faced by these parties. If we operationalize niche parties in a different, more precise manner (the share of the manifesto devoted to left-right topics), the effect loses its significance. A further control variable tabs into the questions of party system compactness: do parties without close neighboring competitors issue broader, more ambiguous platforms? We therefore include a variable that measure the minimal distance to the next competitor. The estimate is positive and significant but the effect is small. Considering that our main findings remain stable even when including these additional controls we are confident that our results are not driven by the fact that centrist parties have less space available and are therefore less ambiguous.

Interpreting parameter estimates in multilevel models can be cumbersome. As both intercept and slopes vary by party system-election in our models, only focusing on estimated average coefficients (commonly referred to as “fixed” effects in multilevel modeling) tells us little about differences in the U-shaped relationship between countries or party systems. Figure 3 therefore shows predicted ambiguity based on the estimated coefficients from Model 1 in each group. More specifically, we combine the average coefficients with group-level errors to compute coefficients at the group level and use these intercepts and slopes to predict the ambiguity of party platforms for each party system-election. The figure shows that the relationship between platform means and ambiguity is U-shaped as expected. There are a small number of groups where there is no discernible relationship (e.g., Denmark 1987 and 1988) and even a few instances where the relationship is slightly inverse U-shaped (e.g., Italy 1983), but these are rare exceptions.

Fig. 3 Relationship between party platform means (z, displayed on the horizontal axis) and party platform ambiguity ( $${\rm log}(\sigma _{\xi } )$$ , displayed on the vertical axis) for 59 party system-elections Note: The lines show predicted platform ambiguity based on Model 1 from Table 2. The theoretical expectation is to find U-shaped regression lines. Swe=Sweden, Den=Denmark, Fin=Finland, Net=the Netherlands, Lux=Luxembourg, Fra=France, Ita=Italy, Spa=Spain, Por=Portugal, Ger=Germany, Aus=Austria, UK=United Kingdom, Ire=Ireland, BeW=Belgium (Walloon), BeF=Belgium (Flanders).

Remarkable is also that the absolute level of ambiguity differs considerably across groups, or, more precisely, across countries. Such cross-national variations in ambiguity levels are not the focus of this study but certainly worth further exploration in future work. Can these differences be attributed to political culture differences or is it simply the language that makes manifestos more or less ambiguous? Important for this study is, however, that position and ambiguity data are comparable within a single country at least as platform measures for all parties in one country are obtained from one and only one estimation. This is exactly why we estimate mixed effects models where the parameters of interest, the coefficients for the party position and the squared party position, can vary across party system-elections.

Finally, one might wonder whether the platform means and standard deviations are independent as, by definition, the variance is a function of the mean. Clearly, the “population” of Wordscores a text is generated from is not normal but has a limited range so that the relation between mean and variance is unknown (Neyman 1926). To test the null hypothesis that the standard deviation is a convex function of the mean, merely as a result of the way we measure the two quantities, we perform a simple simulation test. To this end, we generate hypothetical manifestos for each party taking random samples of words from the set of reference text words in the respective country (manifestos have a length of 1000 words). We then calculate platform means and standard deviations for these texts, run the first model and test for a U-shaped relation between platform means and the dependent variable. We do this 100 times and find no single incidence where the null hypothesis of no U-shaped relation could be rejected.

Conclusion

In election campaigns, ambiguity of actors’ positions is a frequent observation. Political parties and candidates often do not articulate their position in a clear-cut manner but remain vague in what they stand for and what policies they want to implement once in office. In this study, we offer two advances to the current literature on positional ambiguity of political actors. First, we contribute to the theoretical literature on positional ambiguity presenting a formal model of multi-party competition with ambiguous party positioning. We posit that parties make strategic choices on both the position and the level of ambiguity of their platforms. The central intuition is that party leaders use programmatic ambiguity to bridge the demands of their two principals, the general electorate and party activists.

Second, utilizing a new, more direct measure of party ambiguity that is derived from parties’ programmatic statements in electoral manifestos rather than voter perception, and drawing on empirical material from 14 West European democracies, this study shows that the programmatic ambiguity of parties in fact varies in a systematic way. This variation is systematically related to their position vis-à-vis their principals, namely voters and party activists. Positional ambiguity of electoral manifestos is especially widespread for more extreme parties, so exactly when these two principals disagree, that is, different demands for position taking exist.

Such behavior can be seen as a variant of party responsiveness where a party does not (or not only) adapt its policy position in response to voter interests but reacts by adapting the width of its policy stances. Hence, our focus on party ambiguity adds another twist to the more general literature on representation. As ambiguity opens up opportunities for parties to be—seemingly—responsive to their constituencies, we may have to reconsider the quality of (policy) representation in Europe.

Although the fact that parties do react vis-à-vis their principals on multiple dimensions can be seen as a positive sign for the working of representation and democracy more broadly, some note of caution is also warranted. Ambiguous positions of parties make it more difficult for voters to identify the party closest to their own interests and thus to act according to the representational ideal. Thus, too much positional ambiguity potentially becomes a threat for the functioning of electoral democracy. On the other hand, the present study provides evidence that the ambiguity of party positions is not random but within strict spatial limits. Further, it is limited to those parties that face clearly defined trade-offs in their position taking.

Our theoretical model as well as the empirical evidence suggests that more centrist parties display the lowest levels of positional ambiguity—all else being equal. This may seem surprising to some political observers as these parties, often deemed catch-all parties, reportedly appeal to a broad spectrum of voters which might make their communication less precise. However, as our study shows, talking about a broad range of things does not necessarily mean blurring your ideological profile that we measure on the left-right dimension. We believe that our focus on a direct measure of positional ambiguity is an advantage in this respect as it allows distinguishing voters’ perceptions from actual party stances.

A second important finding of this study is that, vice versa, more extreme parties on the left-right dimension have higher levels of positional ambiguity. These results nicely complement previous work on non-centrist parties suggesting that smaller, more extreme parties have incentives to highlight their (more clear cut) positions on single, specific issues (Shepsle 1972; de Vries and Hobolt 2012; de Vries and Marks 2012). If this is correct, our analysis suggests that clear-cut positions on specific issues may well go along with a blurred position on the general ideological dimension. Extending our theoretical and empirical work to a multidimensional space might thus be a promising way to get more leverage on the strategic incentives for parties to present more or less ambiguous positions on several dimensions.

Another interesting avenue for future research opens up when combining our results with the recent finding by Ezrow, Homola and Tavits (2014) that extreme parties are more easily positioned by voters and thus perceived to be less ambiguous than more centrist parties. Exploring this mismatch between the ambiguity of the party program and the perception of ambiguity by voters could be worthwhile.