Article contents
A Coupling Proof of the Asymptotic Normality of the Permutation Oscillation
Published online by Cambridge University Press: 27 July 2009
Abstract
For each n ≥ 1, let Πn = (π1, π2, …, πn) be a random permutation of the integers 1,2, …, n. The quantity Bn = Σ 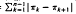 measures the degree of oscillation of Πn and is an important measure in the study of sorting algorithms. In this work the asymptotic normality of Bn is derived under the assumption that, for each n ≥ 1, Πn is uniformly distributed over the n! permutations of 1,2, …, n. The proof relies on coupling (π1, π2, …, πn) with a sequence of independent and identically distributed U(0,1) random variables and offers a more probabilistic and computationally simpler alternative to the method of moments proof of Chao, Bai, and Liang (1993, Probability in the Engineering and Informational Sciences 7: 227–235).
measures the degree of oscillation of Πn and is an important measure in the study of sorting algorithms. In this work the asymptotic normality of Bn is derived under the assumption that, for each n ≥ 1, Πn is uniformly distributed over the n! permutations of 1,2, …, n. The proof relies on coupling (π1, π2, …, πn) with a sequence of independent and identically distributed U(0,1) random variables and offers a more probabilistic and computationally simpler alternative to the method of moments proof of Chao, Bai, and Liang (1993, Probability in the Engineering and Informational Sciences 7: 227–235).
Information
- Type
- Research Article
- Information
- Probability in the Engineering and Informational Sciences , Volume 9 , Issue 4 , October 1995 , pp. 615 - 621
- Copyright
- Copyright © Cambridge University Press 1995
References
- 7
- Cited by

