Hostname: page-component-7dd5485656-frp75 Total loading time: 0 Render date: 2025-10-31T01:08:18.765Z Has data issue: false hasContentIssue false
  • English
  • Français

On history-dependent mixed shock models

Published online by Cambridge University Press:  06 August 2021

Dheeraj Goyal ,
Maxim Finkelstein Open the ORCID record for Maxim Finkelstein [Opens in a new window]  and
Nil Kamal Hazra
Dheeraj Goyal
Affiliation:
Department of Mathematics, Indian Institute of Technology Jodhpur, Karwar, Rajasthan, India.
Maxim Finkelstein
Affiliation:
Department of Mathematical Statistics and Actuarial Science, University of the Free State, 339, Bloemfontein, South Africa. Department of Management Science, University of Strathclyde, Glasgow, UK. E-mail: FinkelM@ufs.ac.za
Nil Kamal Hazra
Affiliation:
Department of Mathematics, Indian Institute of Technology Jodhpur, Karwar, Rajasthan, India. School of AI & DS, Indian Institute of Technology Jodhpur, Karwar, Rajasthan, India
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider a history-dependent mixed shock model which is a combination of the history-dependent extreme shock model and the history-dependent 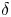$\delta$-shock model. We assume that shocks occur according to the generalized Pólya process that contains the homogeneous Poisson process, the non-homogeneous Poisson process and the Pólya process as the particular cases. For the defined survival model, we derive the corresponding survival function, the mean lifetime and the failure rate. Further, we study the asymptotic and monotonicity properties of the failure rate. Finally, some applications of the proposed model have also been included with relevant numerical examples.

Keywords

δ-shock modelExtreme shock modelOptimal mission durationOptimal replacement policyReliability

Information

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 36 , Issue 4 , October 2022 , pp. 1080 - 1097
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

A-Hameed, M.S. & Proschan, F. (1973). Nonstationary shock models. Stochastic Processes and Their Applications 1: 383–404.CrossRefGoogle Scholar
Cha, J.H. (2014). Characterization of the generalized Pólya process and its applications. Advances in Applied Probability 46: 1148–1171.CrossRefGoogle Scholar
Cha, J.H. & Finkelstein, M. (2009). On a terminating shock process with independent wear increments. Journal of Applied Probability 46: 353–362.CrossRefGoogle Scholar
Cha, J.H. & Finkelstein, M. (2011). On new classes of extreme shock models and some generalizations. Journal of Applied Probability 48: 258–270.CrossRefGoogle Scholar
Cha, J.H. & Finkelstein, M. (2013). On history-dependent shock models. Operations Research Letters 41: 232–237.Google Scholar
Cha, J.H. & Finkelstein, M. (2018). Point processes for reliability analysis: shocks and repairable systems. London: Springer.CrossRefGoogle Scholar
Eryilmaz, S. (2012). Generalized $\delta$-shock model via runs. Statistics and Probability Letters 82: 326–331.CrossRefGoogle Scholar
Eryilmaz, S. (2017). $\delta$-shock model based on Pólya process and its optimal replacement policy. European Journal of Operational Research 263: 690–697.CrossRefGoogle Scholar
Eryilmaz, S. & Bayramoglu, K. (2014). Life behavior of $\delta$-shock models for uniformly distributed interarrival times. Statistical Papers 55: 841–852.CrossRefGoogle Scholar
Eryilmaz, S. & Tekin, M. (2019). Reliability evaluation of a system under a mixed shock model. Journal of Computational and Applied Mathematics 352: 255–261.CrossRefGoogle Scholar
Esary, J.D., Marshall, A.W., & Proschan, F. (1973). Shock models and wear process. The Annals of Probability 1: 627–649.CrossRefGoogle Scholar
Finkelstein, M. & Levitin, G. (2017). Optimal mission duration for systems subject to shocks and internal failures. Proceedings of the Institution of Mechanical Engineers, Part O: Journal of Risk and Reliability 232: 82–91.Google Scholar
Gut, A. (1990). Cumulative shock models. Advances in Applied Probability 22: 504–507.CrossRefGoogle Scholar
Gut, A. & Hüsler, J. (1999). Extreme shock models. Extremes 2: 295–307.CrossRefGoogle Scholar
Gut, A. & Hüsler, J. (2005). Realistic variation of shock models. Statistics and Probability Letters 74: 187–204.CrossRefGoogle Scholar
Lam, Y. & Zhang, Y.L. (2004). A shock model for the maintenance problem of a repairable system. Computers and Operations Research 31: 1807–1820.CrossRefGoogle Scholar
Li, Z. & Kong, X. (2007). Life behavior of $\delta$-shock model. Statistics and Probability Letters 77: 577–587.CrossRefGoogle Scholar
Li, Z., Chan, L.Y., & Yuan, Z. (1999). Failure time distribution under a $\delta$-shock model and its application to economic design of systems. International Journal of Reliability, Quality and Safety Engineering 6: 237–247.CrossRefGoogle Scholar
Li, Z.H., Huang, B.S., & Wang, G.J. (1999). Life distribution and its properties of shock models under random shocks. Journal of Lanzhou University 35: 1–7.Google Scholar
Lorvand, H., Nematollahi, A., & Poursaeed, M.H. (2019). Life distribution properties of a new $\delta$-shock model. Communications in Statistics-Theory and Methods 49: 3010–3025.CrossRefGoogle Scholar
Lorvand, H., Poursaeed, M.H., & Nematollahi, A.R. (2020). On the life distribution behavior of the generalized mixed $\delta$-shock models for the multi-state systems. Iranian Journal of Science and Technology, Transactions A: Science 44: 839–850.CrossRefGoogle Scholar
Mallor, F. & Omey, E. (2001). Shocks, runs and random sums. Journal of Applied Probability 38: 438–448.CrossRefGoogle Scholar
Mallor, F., Omey, E., & Santos, J. (2006). Asymptotic results for a run and cumulative mixed shock model. Journal of Mathematical Sciences 138: 5410–5414.CrossRefGoogle Scholar
Ozkut, M. & Eryilmaz, S. (2019). Reliability analysis under Marshall-Olkin run shock model. Journal of Computational and Applied Mathematics 349: 52–59.CrossRefGoogle Scholar
Parvardeh, A. & Balakrishnan, N. (2015). On mixed $\delta$-shock models. Statistics and Probability Letters 102: 51–60.CrossRefGoogle Scholar
Shanthikumar, J.G. & Sumita, U. (1983). General shock models associated with correlated renewal sequences. Journal of Applied Probability 20: 600–614.CrossRefGoogle Scholar
Shanthikumar, J.G. & Sumita, U. (1984). Distribution properties of the system failure time in a general shock model. Advances in Applied Probability 16: 363–377.CrossRefGoogle Scholar
Tang, Y.Y. & Lam, Y. (2006). A $\delta$-shock maintenance model for a deteriorating system. European Journal of Operational Research 168: 541–556.CrossRefGoogle Scholar
Tuncel, A. & Eryilmaz, S. (2018). System reliability under $\delta$-shock model. Communications in Statistics – Theory and Methods 47: 4872–4880.CrossRefGoogle Scholar
Wang, G.J. & Peng, R. (2016). A generalised $\delta$-shock model with two types of shocks. International Journal of Systems Science: Operations and Logistics 4: 372–383.Google Scholar
Wang, G.J. & Zhang, Y.L. (2005). A shock model with two-type failures and optimal replacement policy. International Journal of Systems Science 36: 209–214.CrossRefGoogle Scholar