Article contents
Stochastic comparison of parallel systems with Pareto components
Published online by Cambridge University Press: 20 May 2021
Abstract
Pareto distribution is an important distribution in extreme value theory. In this paper, we consider parallel systems with Pareto components and study the effect of heterogeneity on skewness of such systems. It is shown that, when the lifetimes of components have different shape parameters, the parallel system with heterogeneous Pareto component lifetimes is more skewed than the system with independent and identically distributed Pareto components. However, for the case when the lifetimes of components have different scale parameters, the result gets reversed in the sense of star ordering. We also establish the relation between star ordering and dispersive ordering by extending the result of Deshpande and Kochar [(1983). Dispersive ordering is the same as tail ordering. Advances in Applied Probability 15(3): 686–687] from support 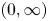 $(0, \infty )$ to general supports
$(0, \infty )$ to general supports 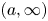 $(a, \infty )$,
$(a, \infty )$, 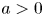 $a > 0$. As a consequence, we obtain some new results on dispersion of order statistics from heterogeneous Pareto samples with respect to dispersive ordering.
$a > 0$. As a consequence, we obtain some new results on dispersion of order statistics from heterogeneous Pareto samples with respect to dispersive ordering.
Information
- Type
- Research Article
- Information
- Probability in the Engineering and Informational Sciences , Volume 36 , Issue 4 , October 2022 , pp. 950 - 962
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press
References
- 2
- Cited by

