No CrossRef data available.
Article contents
STOCHASTIC MONOTONICITY OF CONDITIONAL ORDER STATISTICS IN MULTIPLE-OUTLIER SCALE POPULATION
Published online by Cambridge University Press: 16 November 2016
Abstract
This paper discusses the stochastic monotonicity property of the conditional order statistics from independent multiple-outlier scale variables in terms of the likelihood ratio order. Let X 1, …, X n be a set of non-negative independent random variables with X i , i=1, …, p, having common distribution function F(λ1x), and X j , j=p+1, …, n, having common distribution function F(λ2x), where F(·) denotes the baseline distribution. Let X i:n (p, q) be the ith smallest order statistics from this sample. Denote by 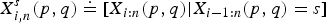 $X_{i,n}^{s}(p,q)\doteq [X_{i:n}(p,q)|X_{i-1:n}(p,q)=s]$ . Under the assumptions that xf′(x)/f(x) is decreasing in x∈ℛ+, λ1≤λ2 and s 1≤s 2, it is shown that
$X_{i,n}^{s}(p,q)\doteq [X_{i:n}(p,q)|X_{i-1:n}(p,q)=s]$ . Under the assumptions that xf′(x)/f(x) is decreasing in x∈ℛ+, λ1≤λ2 and s 1≤s 2, it is shown that 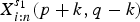 $X_{i:n}^{s_{1}}(p+k,q-k)$ is larger than
$X_{i:n}^{s_{1}}(p+k,q-k)$ is larger than 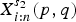 $X_{i:n}^{s_{2}}(p,q)$ according to the likelihood ratio order for any 2≤i≤n and k=1, 2, …, q. Some parametric families of distributions are also provided to illustrate the theoretical results.
$X_{i:n}^{s_{2}}(p,q)$ according to the likelihood ratio order for any 2≤i≤n and k=1, 2, …, q. Some parametric families of distributions are also provided to illustrate the theoretical results.
Information
- Type
- Research Article
- Information
- Probability in the Engineering and Informational Sciences , Volume 31 , Issue 3 , July 2017 , pp. 366 - 380
- Copyright
- Copyright © Cambridge University Press 2016

