Article contents
CHARACTERIZATIONS OF OPTIMAL POLICIES IN A GENERAL STOPPING PROBLEM AND STABILITY ESTIMATING
Published online by Cambridge University Press: 05 June 2014
Abstract
We consider an optimal stopping problem for a general discrete-time process X1, X2, …, Xn, … on a common measurable space. Stopping at time n (n = 1, 2, …) yields a reward Rn(X1, …, Xn) ≥ 0, while if we do not stop, we pay cn(X1, …, Xn) ≥ 0 and keep observing the process. The problem is to characterize all the optimal stopping times τ, i.e., such that maximize the mean net gain: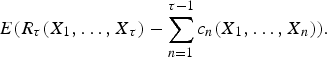 $$E(R_\tau(X_1,\dots,X_\tau)-\sum_{n=1}^{\tau-1}c_n(X_1,\dots,X_n)).$$
$$E(R_\tau(X_1,\dots,X_\tau)-\sum_{n=1}^{\tau-1}c_n(X_1,\dots,X_n)).$$
In the particular case of Markov sequence X1, X2, … we estimate the stability of the optimal stopping problem under perturbations of transition probabilities.
Information
- Type
- Research Article
- Information
- Probability in the Engineering and Informational Sciences , Volume 28 , Issue 3 , July 2014 , pp. 335 - 352
- Copyright
- Copyright © Cambridge University Press 2014
References
- 2
- Cited by

