Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T02:32:26.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Concentrated matrix exponential distributions with real eigenvalues

Published online by Cambridge University Press:  26 August 2021

András Mészáros  and
Miklós Telek Open the ORCID record for Miklós Telek [Opens in a new window]
András Mészáros
Affiliation:
Department of Networked Systems and Services, Technical University of Budapest, Budapest, Hungary. E-mail: meszarosa@hit.bme.hu
Miklós Telek
Affiliation:
Department of Networked Systems and Services, Technical University of Budapest, Budapest, Hungary. E-mail: meszarosa@hit.bme.hu MTA-BME Information Systems Research Group, Budapest, Hungary. E-mail: telek@hit.bme.hu
Get access Rights & Permissions [Opens in a new window]

Abstract

Concentrated random variables are frequently used in representing deterministic delays in stochastic models. The squared coefficient of variation (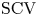$\mathrm {SCV}$) of the most concentrated phase-type distribution of order 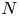$N$ is 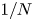$1/N$. To further reduce the 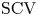$\mathrm {SCV}$, concentrated matrix exponential (CME) distributions with complex eigenvalues were investigated recently. 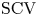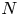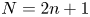It was obtained that the $\mathrm {SCV}$ of an order $N$ CME distribution can be less than $n^{-2.1}$ for odd $N=2n+1$ orders, and the matrix exponential distribution, which exhibits such a low 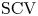$\mathrm {SCV}$ has complex eigenvalues. In this paper, we consider CME distributions with real eigenvalues (CME-R). We present efficient numerical methods for identifying a CME-R distribution with smallest SCV for a given order 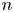$n$. Our investigations show that the 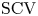$\mathrm {SCV}$ of the most concentrated CME-R of order 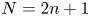$N=2n+1$ is less than 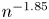$n^{-1.85}$. We also discuss how CME-R can be used for numerical inverse Laplace transformation, which is beneficial when the Laplace transform function is impossible to evaluate at complex points.

Keywords

Concentrated matrix exponential distributionsEigenvaluesMatrix exponential distributionPhase-type distributionSquared coefficient of variation
Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 36 , Issue 4 , October 2022 , pp. 1171 - 1187
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abate, J. & Whitt, W. (2006). A unified framework for numerically inverting Laplace transforms. INFORMS Journal on Computing 18(4): 408–421.CrossRefGoogle Scholar
Abate, J., Choudhury, G.L., & Whitt, W. (2000). An introduction to numerical transform inversion and its application to probability models. In W. K. Grassmann (ed.), Computational probability. Boston, MA: Springer US, pp. 257–323.CrossRefGoogle Scholar
Airapetyan, R.G. & Ramm, A.G. (2000). Numerical inversion of the Laplace transform from the real axis. Journal of Mathematical Analysis and Applications 248(2): 572–587.CrossRefGoogle Scholar
Aldous, D. & Shepp, L. (1987). The least variable phase type distribution is Erlang. Stochastic Models 3: 467–473.Google Scholar
Éltető, T., Rácz, S., & Telek, M. (2006). Minimal coefficient of variation of matrix exponential distributions. In 2nd Madrid Conference on Queueing Theory, Madrid, Spain, July 2006.Google Scholar
Gaver, D.P. (1966). Observing stochastic processes and approximate transform inversion. Operations Research 14: 444–459.CrossRefGoogle Scholar
Hansen, N. (2006). The CMA evolution strategy: a comparing review. In J. A. Lozano, P. Larrañaga, I. Inza, & E. Bengoetxea (eds), Towards a new evolutionary computation. Springer, pp. 75–102.CrossRefGoogle Scholar
Hansen, N. (2009). Benchmarking a BI-population CMA-ES on the BBOB-2009 function testbed. In Proceedings of the 11th Annual Conference Companion on Genetic and Evolutionary Computation Conference: Late Breaking Papers. ACM, pp. 2389–2396. https://doi.org/10.1145/1570256.1570333CrossRefGoogle Scholar
Horváth, I., Horváth, G., Al-Deen Almousa, S., & Telek, M. (2019). Numerical inverse Laplace transformation by concentrated matrix exponential distributions. Performance Evaluation 137: 102067.CrossRefGoogle Scholar
Horváth, G., Horváth, I., & Telek, M. (2020). High order concentrated matrix-exponential distributions. Stochastic Models 36(2): 176–192.CrossRefGoogle Scholar
Keller, H.B. & Pereyra, V. (1978). Symbolic generation of finite difference formulas. Mathematics of Computation 32(144): 955–971.CrossRefGoogle Scholar
Koskela, H., Kilpeläinen, I., & Heikkinen, S. (2004). Evaluation of protein $^{1}5$N relaxation times by inverse Laplace transformation. Magnetic Resonance in Chemistry 42(1): 61–65.CrossRefGoogle Scholar
Nishiyama, Y., Frey, M.H., Mukasa, S., & Utsumi, H. (2010). $^{1}3$C solid-state NMR chromatography by magic angle spinning $^{1}$H $T_1$ relaxation ordered spectroscopy. Journal of Magnetic Resonance 202(2): 135–139.CrossRefGoogle Scholar
Stehfest, H. (1970). Algorithm 368: Numerical inversion of Laplace transforms [D5]. Communications of the ACM 13(1): 47–49.CrossRefGoogle Scholar
Valko, P. & Abate, J. (2004). Comparison of sequence accelerators for the Gaver method of numerical Laplace transform inversion. Computers and Mathematics with Applications 48: 629–636.CrossRefGoogle Scholar