Article contents
DRAWING MULTISETS OF BALLS FROM TENABLE BALANCED LINEAR URNS
Published online by Cambridge University Press: 28 March 2013
Abstract
We investigate the evolution of an urn of balls of two colors, where one chooses a pair of balls and observes rules of ball addition according to the outcome. A nonsquare ball addition matrix of the form 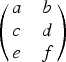 $\left( \matrix{a & b \cr c & d \cr e & f}\right)$ corresponds to such a scheme, in contrast to pólya urn models that possess a square ball addition matrix. We look into the case of constant row sum (the so-called balanced urns) and identify a linear case therein. Two cases arise in linear urns: the nondegenerate and the degenerate. Via martingales, in the nondegenerate case one gets an asymptotic normal distribution for the number of balls of any color. In the degenerate case, a simpler probability structure underlies the process. We mention in passing a heuristic for the average-case analysis for the general case of constant row sum.
$\left( \matrix{a & b \cr c & d \cr e & f}\right)$ corresponds to such a scheme, in contrast to pólya urn models that possess a square ball addition matrix. We look into the case of constant row sum (the so-called balanced urns) and identify a linear case therein. Two cases arise in linear urns: the nondegenerate and the degenerate. Via martingales, in the nondegenerate case one gets an asymptotic normal distribution for the number of balls of any color. In the degenerate case, a simpler probability structure underlies the process. We mention in passing a heuristic for the average-case analysis for the general case of constant row sum.
Information
- Type
- Research Article
- Information
- Probability in the Engineering and Informational Sciences , Volume 27 , Issue 2 , April 2013 , pp. 147 - 162
- Copyright
- Copyright © Cambridge University Press 2013
References
- 11
- Cited by

