Article contents
Likelihood ratio comparisons and logconvexity properties of p-spacings from generalized order statistics
Published online by Cambridge University Press: 25 November 2021
Abstract
Due to the importance of generalized order statistics (GOS) in many branches of Statistics, a wide interest has been shown in investigating stochastic comparisons of GOS. In this article, we study the likelihood ratio ordering of 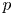 $p$-spacings of GOS, establishing some flexible and applicable results. We also settle certain unresolved related problems by providing some useful lemmas. Since we do not impose restrictions on the model parameters (as previous studies did), our findings yield new results for comparison of various useful models of ordered random variables including order statistics, sequential order statistics,
$p$-spacings of GOS, establishing some flexible and applicable results. We also settle certain unresolved related problems by providing some useful lemmas. Since we do not impose restrictions on the model parameters (as previous studies did), our findings yield new results for comparison of various useful models of ordered random variables including order statistics, sequential order statistics, 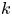 $k$-record values, Pfeifer's record values, and progressive Type-II censored order statistics with arbitrary censoring plans. Some results on preservation of logconvexity properties among spacings are provided as well.
$k$-record values, Pfeifer's record values, and progressive Type-II censored order statistics with arbitrary censoring plans. Some results on preservation of logconvexity properties among spacings are provided as well.
Keywords
Information
- Type
- Research Article
- Information
- Probability in the Engineering and Informational Sciences , Volume 37 , Issue 1 , January 2023 , pp. 86 - 105
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press
References
- 5
- Cited by

