Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T04:45:06.719Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SKEWNESS AND DISPERSION AMONG CONVOLUTIONS OF INDEPENDENT GAMMA RANDOM VARIABLES

Published online by Cambridge University Press:  02 November 2010

Leila Amiri ,
Baha-Eldin Khaledi  and
Francisco J. Samaniego
Leila Amiri
Affiliation:
Department of Statistics, Razi University, Kermanshah, Iran E-mail: bkhaledi@hotmail.com
Baha-Eldin Khaledi
Affiliation:
Department of Statistics, Razi University, Kermanshah, Iran E-mail: bkhaledi@hotmail.com
Francisco J. Samaniego
Affiliation:
Department of Statistics, University of California, Davis, CA
Get access Rights & Permissions [Opens in a new window]

Abstract

Let {x(1)≤···≤x(n)} denote the increasing arrangement of the components of a vector x=(x1, …, xn). A vector x∈Rn majorizes another vector y (written 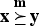) if 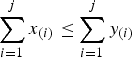for j = 1, …, n−1 and 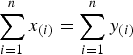. A vector x∈R+n majorizes reciprocally another vector y∈R+n (written 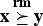) if 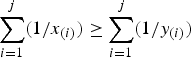for j = 1, …, n. Let , be n independent random variables such that is a gamma random variable with shape parameter α≥1 and scale parameter λi, i = 1, …, n. We show that if 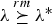, then 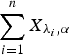is greater than 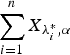according to right spread order as well as mean residual life order. We also prove that if 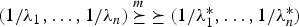, then 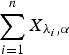is greater than 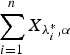according to new better than used in expectation order as well as Lorenze order. These results mainly generalize the recent results of Kochar and Xu [7] and Zhao and Balakrishnan [14] from convolutions of independent exponential random variables to convolutions of independent gamma random variables with common shape parameters greater than or equal to 1.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 25 , Issue 1 , January 2011 , pp. 55 - 69
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Barlow, R.E. & Proschan, F. (1981). Statistical theory of reliability and life testing. Silver Spring, MD. To Begin with.Google Scholar
2.Denuit, M., Dhaene, J., Goovaerts, M. & Kaas, R. (2005). Actuarial theory for dependent risks. Chichester, UK: Wiley.CrossRefGoogle Scholar
3.Dharmadhikari, S. & Joeg-Dev, K. (1988). Unimodality, convexity and applications. New York: Academic Press.Google Scholar
4.Fernández-Ponce, J.M., Kochar, S.C. & Muñoz-Perez, J. (1998). Partial orderings of distributions based on right-spread functions. Journal of Applied Probability 35: 221–228.CrossRefGoogle Scholar
5.Khaledi, B.E. & Kochar, S.C. (2004). Ordering convolutions of gamma random variables. Sankhyā 66: 466–473.Google Scholar
6.Kochar, S., Li, X. & Shaked, M. (2002). The total time on test transform and excess wealth stochastic order of distributions. Advances in Applied Probability 34: 826–845.CrossRefGoogle Scholar
7.Kochar, S. & Xu, M. (2009). On the right spread order of convolutions of heterogeneous exponential random variables. Journal of Multivariate Analysis 101: 165–179.CrossRefGoogle Scholar
8.Korwar, R.M. (2002). On Stochastic orders for sums of independent random variables. Journal of Multivariate Analysis 80: 344–357.CrossRefGoogle Scholar
9.Lorch, L. (1967). Inequalities for some Whittaker functions. Archiv der Mathematik 3: 1–9.Google Scholar
10.Marshall, A.W. & Olkin, I. (1979). Inequalities: Theory of majorization and its applications. New York: Academic Press.Google Scholar
11.Marshall, A.W. & Olkin, I. (2007). Life distributions. New York: Springer.Google Scholar
12.Saunders, I.W. & Moran, P.A. (1978). On the quantiles of gamma and F distributions. Journal of Applied Probability 15: 426–432.CrossRefGoogle Scholar
13.Shaked, M. & Shanthikumar, J. G. (2007). Stochastic orders and their applications. New York: Springer.Google Scholar
14.Zhao, P. & Balakrishnan, N. (2009). Mean residual life order of convolutions of heterogenous exponential random variables. Journal of Multivariate Analysis 100: 1792–1801.CrossRefGoogle Scholar
15.Kochar, S. & Xu, M. (2011). The tail behavior of convolutions of gamma random variables. Journal of Statistical Planning and Inference 141: 418–428.CrossRefGoogle Scholar