SCHEDULING IN A QUEUING SYSTEM WITH ASYNCHRONOUSLY VARYING SERVICE RATES

Abstract

We consider the following queuing system which arises as a model of a wireless link shared by multiple users. There is a finite number N of input flows served by a server. The system operates in discrete time t = 0,1,2,…. Each input flow can be described as an irreducible countable Markov chain; waiting customers of each flow are placed in a queue. The sequence of server states m(t), t = 0,1,2,…, is a Markov chain with finite number of states M. When the server is in state m, it can serve μ_i^m customers of flow i (in one time slot).

The scheduling discipline is a rule that in each time slot chooses the flow to serve based on the server state and the state of the queues. Our main result is that a simple online scheduling discipline, Modified Largest Weighted Delay First, along with its generalizations, is throughput optimal; namely, it ensures that the queues are stable as long as the vector of average arrival rates is within the system maximum stability region.

1. INTRODUCTION

We consider a model motivated by the problem of scheduling transmissions of multiple data users (flows) sharing the same wireless channel (server). The unique “wireless” feature of this problem is the fact that the capacity (service rate) of the channel varies with time randomly and asynchronously for different users. The variations of the channel capacity are due to different, random interference levels observed by different users and due to fast fading of the signal received by a user. We will refer to this problem as the variable channel scheduling problem.

The variable channel problem arises, for example, in the 3G CDMA High Data Rate (HDR) system [6]. (See also [27] for a background on CDMA wireless systems.) In HDR, multiple mobile users in a cell share the same CDMA wireless channel. On the downlink (the link from the cell base station to users), time is divided into fixed-size (1.67-ms) time slots. This slot size is short enough so that (each user's) channel quality stays approximately constant within one or even a few consecutive time slots. (To be more precise, this is true only for relatively low mobile user velocities; see [27].) In each time slot, data can be transmitted to only one user. Each user constantly reports to the base station its “instantaneous” channel capacity (i.e., the rate at which data can be transmitted if this user is scheduled for transmission in the current time slot).

In the HDR system (and in the generic variable channel model as well), a scheduling algorithm can take advantage of channel variations by giving some form of priority to users with (temporarily) better channels. Since channel capacities of different users vary in time in an asynchronous manner, the quality of service (QoS) of all users can be improved, as compared to scheduling schemes which do not take channel conditions into account. A scheduling rule providing proportional fairness in the achieved long-term throughput of different users was proposed and analyzed in [25]. (See also [26].)

The QoS of a data user can be defined in different ways. If data users are real-time users, then the packet delays of each flow need to be kept below a certain threshold. This means that the primary goal of a scheduling algorithm is to keep all queues stable (i.e., to be able to handle all the offered traffic without queues “blowing up”).

In this article, we consider the generic variable channel scheduling model. Our main result is that a simple online scheduling discipline, modified largest weighted delay first (M-LWDF), is throughput optimal; namely it ensures that the queues are stable as long as the vector of average arrival rates is within the system's maximum stability region.

In a time slot t, the M-LWDF discipline serves the flow j for which

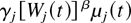
is maximal, where W_j(t) is the head-of-the-line packet delay for flow j, μ_j(t) is the server capacity for flow j at time t, and β and the γ_j's are arbitrary positive constants. (The name M-LWDF is because this discipline is a generalization of the LWDF discipline [1,22].) Moreover, as we discuss in Section 4, our result actually holds for a quite wide class of disciplines (of which M-LWDF is a member) and a more general class of models. In particular, the throughput optimality holds if instead of maximizing (1), the scheduling rule maximizes

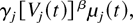
where V_j(t) = η_j^(W)W_j(t) + η_j^(Q)Q_j(t). Here, η_j^(W) ≥ 0 and η_j^(Q) ≥ 0 are arbitrary parameters for flow j, not equal to zero simultaneously and possibly dependent on j.

Our main stability results are closely related to the series of results on the stability of MaxWeight-type scheduling algorithms in queuing networks and in input-buffered crossbar switches. The first results of this type were obtained by Tassiulas and Ephremides [23,24] in the context of wireless systems. For the switch scheduling stability results, see [15,17] and a recent paper [10]. In the context of interactive parallel server systems and systems with randomly varying connectivity, MaxWeight-type stability results were obtained in [3,5]. (See also [4], which is a recent extension of [3].)

The underlying intuition behind the stability of a MaxWeight-type algorithm is the fact that it minimizes the drift of a Lyapunov function of the form [sum ]_j[V_j(t)]^β+1. Most of the algorithms studied before are for the case β = 1 and V_j(t) = Q_j(t). As far as we are aware, [17] was the first in which the stability result for a MaxWeight-type rule using flow delays W_j(t) (as opposed to queue lengths Q_j(t)) was derived. (A similar result was formulated but not proved in [14].)

The main contribution of this article is that we show that a MaxWeight-type algorithm retains stability properties even if the “weight” of an individual queue j has a form as general as [V_j(t)]^β. Such a generalization is important because the additional parameters β, η_j^(W), and η_j^(Q) allow for a more flexible control of queue lengths and delay distributions, to satisfy a variety of QoS constraints. For example, if we are interested in giving tight delay bounds to a flow j with a low arrival rate, then the “weight” for flow j should be based more on head-of-the-line packet delay than on queue length (i.e., η_j^(W) should be large relative to η_j^(Q)). Conversely, if flow j has a high arrival rate and we want to bound its buffer space requirements, then η_j^(Q) should be large relative to η_j^(W).

To prove our stability results, we use the fluid limit technique [7,8,9,19,20]. (For a MaxWeight-type rule, the technique was also used in [10] in a “switch” model context.) Use of this technique makes the above-described generalization very natural. Roughly speaking, in the “fluid limit” and after some initial period of time, Q_j(t) and W_j(t) stay proportional to each other; thus, MaxWeight algorithms using Q_j(t), W_j(t), or a linear combination V_j(t) are in some sense “indistinguishable” in the fluid limit.

It is shown recently in [21], which analyzes a more general (described in Section 4.2) version of our model, that, in addition to throughput optimality, MaxWeight-type rules have certain asymptotic optimality properties when the system is heavily loaded.

Practical implications of using M-LWDF to provide QoS for real-time data users are addressed in [2]. In particular, we show in [2] that the M-LWDF discipline, with “appropriately” chosen parameters γ_i, provides good QoS defined in terms of the probabilities of packet delays exceeding predefined thresholds.

The rest of the article is organized as follows. In Section 2, we introduce the formal variable channel scheduling queuing model. Necessary and sufficient stability conditions are derived and the system stability region is defined in Section 3. In Section 4, we introduce the M-LWDF scheduling rule and formulate our main result—Theorem 3, which states that M-LWDF (along with a wide class of rules generalizing it) is throughput optimal. The proof of Theorem 3 is presented in Section 5.

2. VARIABLE CHANNEL SCHEDULING MODEL

Consider the following queuing system. There is a finite number N of input flows, indexed by i = 1,2,…, N, served by a server. Each input flow consists of discrete customers. (One customer models one byte or bit of data). The system operates in discrete time t = 0,1,2,…. By convention, we will

(a) identify an (integer) time t, with the unit time interval [t,t + 1), which will sometimes be referred to as the time slot t

(b) assume that all processes we consider are constant within each time slot.

There is a finite set {1,…,M} of server states. This set itself we also denote by M (as well as its cardinality). Associated with each state m ∈ M is a fixed vector of service rates (μ₁^m,…, μ_N^m), where all μ_i^m are nonnegative integers. The meaning of μ_i^m is as follows. If in time slot t the server is in state m and the service (in this time slot) is given exclusively to queue i, then μ_i^m type i customers are served from those present at time t (or the entire queue i content at t, whichever is less). We assume that, within each type, customers are served in the order of their arrival in the system.

The random server state process m = m(t), t = 0,1,2,… is assumed to be an irreducible (see [12]) discrete-time Markov chain with the (finite) state space M. The (unique) stationary distribution of this Markov chain we denote by π = (π₁,…, π_M). Note that, due to irreducibility, π_m > 0 for all m ∈ M.

We make a nondegeneracy assumption that for each flow i, there is at least one server state m ∈ M such that μ_i^m > 0. (Otherwise, we would have flows which simply can never be served.)

Denote by A_i(t) the number of type i customers that arrived at time t, and assume by convention that these customers are immediately available for service. We assume that each input process A_i is an irreducible positive recurrent (see [12]) Markov chain with countable state space and that the input processes are mutually independent. (This condition can be relaxed as follows. The aggregate arrival process A = {(A₁(t),…, A_N(t)), t = 1,2,…} can be described by a finite number of regenerative processes [12] with finite mean regeneration cycles.) Let us denote by λ_i, i = 1,…,N, the mean arrival rate for flow i (i.e., the mean number of type i customers arriving in one time slot). The vector of mean arrival rates is denoted by λ [esdot ] (λ₁,…, λ_N).

The random process describing the behavior of the entire system is (S = S(t), t = 0,1,2,…), where

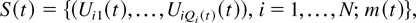
Q_i(t) is the type i queue length at time t, and U_ik(t) is the current sojourn time, or delay, of the kth type i customer present in the system at time t. (Within each type, the customers are numbered in the order of their arrival.)

A mapping H which takes a system state S(t) in a time slot into a fixed probability distribution H(S(t)) on the set of queues N will be called a scheduling rule, or a queuing discipline. With a fixed discipline H, the queue to serve at time t is chosen randomly according to the distribution H(S(t)). So, the number D_i(t) of type i customers served in the time slot t is equal to min{Q_i(t), μ_i^m(t)} if queue i is chosen for service and equal to zero otherwise. According to our conventions, for each time t,

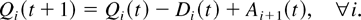
Our assumptions imply that with any scheduling rule, S is a discrete-time countable Markov chain. By stability of the Markov chain S (and stability of the system) we mean the following property: The set of positive recurrent states is nonempty and it contains a finite subset which is reached with probability one (within finite time) from any initial state. Stability implies the existence of a stationary probability distribution. (If all positive recurrent states are connected, the stationary distribution is unique.)

We conclude this section with some basic notation we use throughout the article. Vector inequalities are understood componentwise; [lfloor ]z[rfloor ] and [lceil ]z[rceil ] denote the integer part and the “ceiling” of a real number z, respectively. We say that a function f (t) of a real variable t is RCLL if it is right-continuous and has left limit in every point t of its domain. The abbreviation “u.o.c.” in a convergence statement means that the convergence is uniform on any fixed compact subset of the corresponding function domain. We denote by

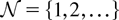
the set of positive natural numbers.

3. NECESSARY AND SUFFICIENT STABILITY CONDITIONS. STABILITY REGION

Suppose a stochastic matrix φ = (φ_mi, m ∈ M, i = 1,…, N) is fixed, which means that φ_mi ≥ 0 for all m and i, and [sum ]_i φ_mi = 1 for every m. Consider a static service split (SSS) scheduling rule, parameterized by the matrix φ. When the server is in state m, the SSS rule chooses for service queue i with probability φ_mi. (The word static in the name of the rule reflects the fact that scheduling decisions depend only on the server state.) Clearly, the vector v = (v₁,…,v_N) = v(φ), where

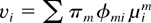
gives the long-term average service rates allocated to different flows. This observation makes the following simple (and quite standard) result very intuitive.

Theorem 1: For the existence of a scheduling rule H under which the system is stable, condition (3) is necessary

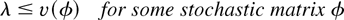
and condition (4) is sufficient

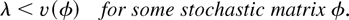
Proof: The necessity of condition (3) is almost obvious. Consider a rule H under which the system is stable and consider the Markov chain S in a stationary regime. (Such a stationary regime exists, but is not necessarily unique.) We will denote by H_i(s) the probability with which the SSS rule chooses for service the queue i when S(t) = s. Then, for any i (and arbitrary fixed time slot t), we can write

Obviously, we have [sum ]_i φ_mi = 1 for each m. The necessity of (3) is proved.

Sufficiency of condition (4) is almost obvious as well. The SSS rule associated with any matrix φ satisfying (4) makes the system stable. Indeed, the rates at which service is provided to different flows i is a random process “modulated” by the underlying (ergodic) Markov chain m, independent of the aggregate arrival process A. Moreover, the average service rate v_i(φ) available to each flow i is strictly greater than its average arrival rate λ_i. If the Markov chain of interest would be

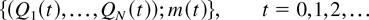
(viz. its states would track queue lengths only), then, for example, max_i Q_i(t) can be used as a Lyapunov function to show the stability via standard “drift” criteria, such as those in [18]. However, the states of our Markov chain S include customer sojourn times as well. To accommodate this, the stability proof for the SSS rule (assuming (4)) can be obtained, for example, as a much simplified version of the proof of M-LWDF rule stability (Theorem 3), which is the main result of this article. Since such a proof requires a fair amount of preliminaries, introduced later in the article, we present its details in the Appendix for the interested reader. (We also note that Theorem 3 itself implies sufficiency of (4). It is, however, more intuitive, simple, and standard to demonstrate this fact via the SSS rule or a similar static rule. That is why we discuss the SSS rule here.) █

The set of all (average arrival rate) vectors λ satisfying condition (4) is usually called the system maximum stability region, or just stability region.

An SSS rule associated with stochastic matrix φ* will be called maximal if the vector v(φ*) is not dominated by v(φ) for any other stochastic matrix φ. (We say that vector v⁽¹⁾ is dominated by vector v⁽²⁾ if v_i⁽¹⁾ ≤ v_i⁽²⁾ for all i and the strict inequality v_i⁽¹⁾ < v_i⁽²⁾ holds for at least one i.) The following theorem provides a useful characterization of maximal SSS rules.

Theorem 2: Consider a maximal SSS rule associated with a stochastic matrix φ*. Suppose, in addition, that all components of v* = v(φ*) are strictly positive. Then, there exists a set of strictly positive constants α_i, i = 1,2,…,N, such that for any m and i,

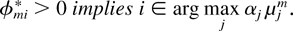
The theorem says that a maximal SSS rule always chooses for service at any time t a queue i for which α_i μ_i^m(t) is maximal. (It does not say what to do in case of a tie.)

Proof: Consider the following linear program:

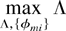
subject to

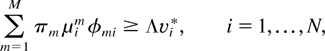
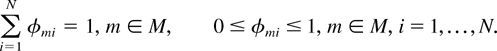
From the definition of v*, we know that Λ = 1 and φ = φ* solve this linear program, with constraints (6) satisfied as equalities. Then, by the Kuhn–Tucker theorem (see, e.g., [13]), there exists a set of nonnegative Lagrange multipliers α₀, α₁,…, α_N such that Λ = 1 and φ = φ* also solve the following linear program (with the same value of the maximum):

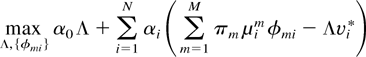
subject to

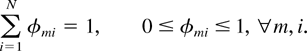
It is easy to verify that all α_i must be strictly positive and α₀ = 1. Then, rewriting (8) as

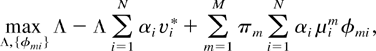
we see that condition (5) must hold, because otherwise the maximum would not be achieved by φ = φ*. █

4. THE MODIFIED LARGEST WEIGHTED DELAY FIRST DISCIPLINE

4.1. Main Result

The following natural question arises. Is there a scheduling rule which (unlike SSS) does not use a priori information about the input rates λ_i and the stationary distribution π of the server state, and yet ensures system stability as long as the necessary and sufficient stability condition (4) is satisfied. Theorem 3 shows that the answer is yes.

Let us call the value

(with W_i(t) = 0 if Q_i(t) = 0 by convention) the delay of flow i at time t.

Let a set of positive constants γ₁,…, γ_N and a positive constant β > 0 be fixed. We define modified largest weighted delay first (M-LWDF) to be the scheduling rule that chooses for service in time slot t a single queue

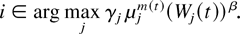
(The “ties” are broken arbitrarily; for example, in favor of the largest index i.)

An analogous rule, which we will call modified largest weighted (unfinished) work first (M-LWWF), chooses a single queue

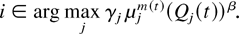
Theorem 3: Let an arbitrary set of positive constants γ₁,…,γ_N and β > 0 be fixed. Then, either of the two scheduling rules, M-LWDF or M-LWWF, are throughput optimal; namely, they make the system stable as long as condition (4) holds (i.e., as long as the arrival rate vector λ is within the system stability region).

As mentioned in Section 1, our proof of Theorem 3 uses the fluid limit technique. This technique allows us to “derive” the stability of M-LWDF from the stability of M-LWWF using the fact that their fluid limits are in a certain sense indistinguishable.

4.2. Generalizations

It will be clear from the proof of Theorem 3 that this result can be significantly generalized. First, the (virtually unchanged) proof allows us to show throughput optimality of the following “mixed” M-LWDF/M-LWWF rule:

Serve queue

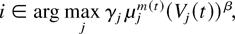
where V_j = η_j^(W)W_j + η_j^(Q)Q_j, and η_j^(W) and η_j^(Q) are nonnegative constants that satisfy η_j^(W) + η_j^(Q) > 0.

In addition, the model assumption that only one queue may be served at a time can be relaxed as follows. For each server state m, there is an associated finite set K(m) of service rate decisions. Associated with each decision k ∈ K(m) is a service rate vector

If the decision k is chosen when the server is in state m, then μ_j^m(k) customers from each queue j (or the entire queue j content Q_j(t) if it is less than μ_j^m(k)) are served within one time slot. Again, a slightly adjusted proof of Theorem 3 allows us to prove that the following MaxWeight-type rule is throughput optimal:

Choose a service rate decision

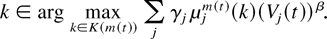
In the latter general form, our result includes as special cases the throughput optimality results in both the “switch scheduling” model setting [15,17] (and related ones in [3,14]) and the variable channel scheduling setting, which is the main focus of this article.

5. PROOF OF THEOREM 3

Throughout the proof, we consider a system with a fixed set of parameters such that condition (4) holds. It needs to be proved that this system is stable under both M-LWDF and M-LWWF rules.

To simplify notation, the proof will be for the case β = 1. The generalization of the proof for arbitrary β > 0 is trivial: The quadratic Lyapunov function in (36) needs to be replaced by the power law function

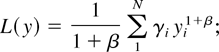
in the formulations of Lemmas 2 and 6, q_i(t), q_j(t), w_i(t), and w_j(t) need to be replaced by q_i(t)^β, q_j(t)^β, w_i(t)^β, and w_j(t)^β, respectively; corresponding minor adjustments need to be made throughout the proofs.

5.1. Preliminaries

Let us define the norm of the state S(t) as follows:

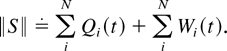
Let S⁽ⁿ⁾ denote a process S with an initial condition such that ∥S⁽ⁿ⁾(0)∥ = n. In the analysis to follow, all variables associated with a process S⁽ⁿ⁾ will be supplied with the upper index (n).

The following theorem follows from the state-dependent Lyapunov-type stability criteria for countable Markov chains, obtained first by Malyshev and Menshikov [16].

Theorem 4: Suppose that there exist ε > 0 and an integer T > 0 such that for any sequence of processes {S⁽ⁿ⁾,n = 1,2,…}, we have

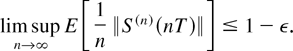
Then, S is stable.

It was shown by Rybko and Stolyar [19] that a stability condition of the type (10) naturally leads to a fluid-limit approach to the stability problem of queuing systems. This approach was further developed by Dai [8], Chen [7], Stolyar [20], and Dai and Meyn [9]. As the form of (10) suggests, the approach studies a fluid process s(t) obtained as a limit of the sequence of scaled processes (1/n)S⁽ⁿ⁾(nt),t ≥ 0. At the heart of the approach in its standard form is a proof that any s(t) starting from any initial state with norm ∥s(0)∥ = 1 reaches zero in finite time T and stays there. It is sufficient, however, to show that for some ε > 0, ∥s(T)∥ ≤ 1 − ε, which is what we are going to do in this article. (In many cases of interest, a still weaker condition is sufficient: It is enough to verify that any s(t) is such that inf_t≥0∥s(t)∥ < 1, as shown in [20]. This is true in our case as well, as could be shown with a little extra work.) In our setting, we need to define what the scaling (1/n)S⁽ⁿ⁾(nt) means. In order for this scaling to make sense, we will need an alternative definition of the process.

To this end, let us define the following random functions associated with the process S⁽ⁿ⁾(t). Let F_i⁽ⁿ⁾(t) be the total number of type i customers that arrived by time t ≥ 0, including the customers present at time 0, and let

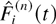
be the number of type i customers that were served by time t ≥ 0. Obviously,

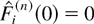
for all i. As in [19] and [20], we “encode” the initial state of the system; in particular, we extend the definition of F_i⁽ⁿ⁾(t) to the negative interval t ∈ [−n,0) by assuming that the customers present in the system in its initial state S⁽ⁿ⁾(0) arrived in the past at some of the time instants −(n − 1),−(n − 2),…,0, according to their delays in the state S(0). By this convention, F_i⁽ⁿ⁾(−n) = 0 for all i and n and

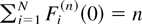
. Also, denote by G_m⁽ⁿ⁾(t) the total number of time slots before time t (i.e., among the slots 0,1,…,t − 1), when the server was in state m, and by

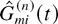
the number of time slots before time t when the server state was m and the server was allocated to serve queue i. Let us also denote

Then, the following relations obviously hold:

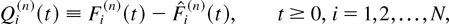
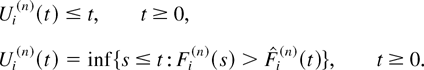
It is clear that the process

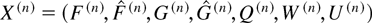
, where

In other words, a sample path of X⁽ⁿ⁾ uniquely defines the sample path of S⁽ⁿ⁾.

Let us also adopt the convention

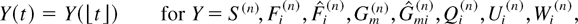
with t ≥ −n for Y = F_i⁽ⁿ⁾ and t ≥ 0 for all other functions. This convention allows us to view the above functions as continuous-time processes defined for all t ≥ 0 (or t ≥ −n), but having constant values in each interval [t,t + 1).

Now, consider the scaled process

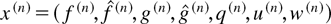
, where

and the scaling is defined as

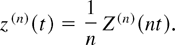
From (11), we get

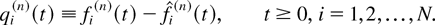
The following lemma establishes convergence to a fluid process and is a variant of Theorem 4.1 in [8]. The lemma is a list of basic convergence properties of the scaled sequences {x⁽ⁿ⁾} which we need for future reference. Although the lemma statement is quite long, the properties it describes are rather simple because they follow almost directly from the structure of the model and the strong law of large numbers for the input flow and server state processes.

Lemma 1: Consider our system under any scheduling rule such that, within each type i, the customers are served in the order of their arrival in the system. The following statements hold with probability 1. For any sequence of processes

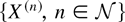
, there exists a subsequence

such that as k → ∞, the scaled subsequence

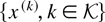
has the following convergence properties for each i ∈ {1,…,N} and m ∈ M:

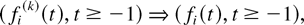
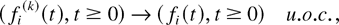
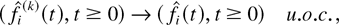
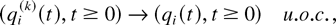
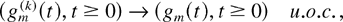
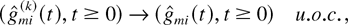
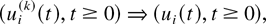
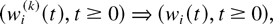
where the functions f_i are RCLL nonnegative nondecreasing in [−1,∞), the functions

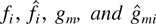
are nonnegative nondecreasing Lipschitz-continuous in [0,∞), functions q_i are continuous in [0,∞), functions u_i are nondecreasing RCLL in [0,∞), functions w_i are nonnegative RCLL in [0,∞), and “⇒” signifies convergence at every continuity point of the corresponding limit function. The limiting set of functions

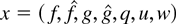
also satisfies the following properties for all i ∈ {1,…,N} and m ∈ M:

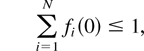
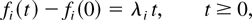
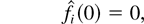
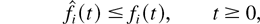
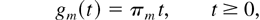
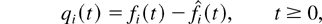
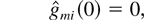
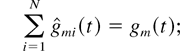
for any interval [t₁,t₂] ⊂ [0,∞),

if q_i(t) > 0 for t ∈ [t₁,t₂] ⊂ [0,∞), then

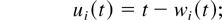
for any fixed t₁ > 0, the conditions

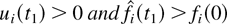
are equivalent and if they hold, then in the interval [t₁,∞),

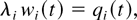
which, in particular, implies that w_i and u_i are Lipschitz-continuous in [t₁,∞).

Remark: The sets of functions x are (“fluid”) limits of the sequences of scaled paths {x^(k)}. As such, its components have the usual natural interpretations. For example,

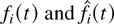
are the amounts of type i “fluid” that arrived into the system and are served by the system by the (scaled) time t, respectively, and

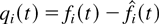
is the amount of unserved type i at time t; g_m(t) is the total (scaled) time before time t when the server state was m;

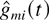
is the total (scaled) time before time t when the server state was m and queue i was chosen for service. Property (23) then means that after time 0, the fluid of each type arrives at the constant rate λ_i; this is generally not true for the interval [−1,0] because the fluid arrival processes f_i(t) in this interval simply code sojourn times of the customers present at time 0, and these initial sojourn times can be distributed in a “bad” way. Inequality (30) simply means that the amount of fluid served in any interval cannot exceed the “potential” amount which could be served if the server would never incur idleness while serving queue i (the idleness is incurred when queue i is served in a slot at the rate μ_i^m, but there are less than μ_i^m customers in the queue); inequality (31) means that if the amount of unserved fluid q_i(t) in some (scaled) interval is bounded away from zero, then the actual amount of fluid served in this interval is exactly equal to the potential amount of service. The property containing (33) is also simple, but is particularly important for our analysis: It says that if by some fixed (scaled) time t₁, the amount of type i fluid served is greater than its initial amount (in particular, all of the “initial fluid” is “gone” by time t₁), then for all t ≥ t₁, the strict linear relation λ_i w_i(t) = q_i(t) exists between the amount of fluid q_i(t) and the “head-of-the-line” fluid delay w_i(t). It is this relation which will allow us to, roughly speaking, make a “transition” from the stability of M-LWWF to the stability of M-LWDF by showing that the fluid limit under M-LWDF is in a certain sense indistinguishable from that under M-LWWF, after the system “gets rid” of all the initial fluid.

Proof of Lemma 1: It follows from the strong law of large numbers that, with probability 1 for every i,

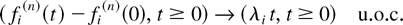
To prove (15), (22), and (23), it suffices to choose a subsequence {x^(k)} such that for every i, lim f_i^(k)(0) exists, and denote the limit by f_i(0). Since all f_i^(k) and u_i^(k) are nondecreasing, we can always choose a further subsequence such that (14) and (20) hold. Then, (21) follows from (20).

Properties (18) and (26) follow from the ergodicity of the server state process.

Also, for any fixed 0 ≤ t₁ ≤ t₂, for every i, m, and any n, we have (using the notation μ* [esdot ] max_m,j μ_j^m)

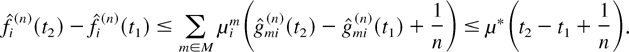
From this inequality, we deduce the existence of a subsequence (of the subsequence already chosen) such that the convergences (16) and (19) take place and (30) holds.

Relations (24), (25), (28), (29), and (32) follow from the corresponding relations which trivially hold for the prelimit functions (for any index

. The convergence (17) and identity (27) trivially follow from identity (13).

Suppose that q_i(t) > 0 for t ∈ [t₁,t₂] ⊂ [0,∞). Let us fix δ ∈ (0,min_t∈[t1,t2] q_i(t)). The Lipschitz continuity of q_i(·), along with u.o.c. convergence of q_i^(k) to q_i, implies that (with probability 1) the sequence {X^(k)} is such that for all sufficiently large k, the following inequalities hold:

The latter property implies that if the queue i was chosen for service anywhere in the interval [[lfloor ]t₁ k[rfloor ],t₂ k + 1] when the server state was m, then exactly μ_i^m type i customers were served. So, we must have

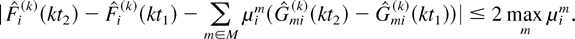
Multiplying the last inequality by 1/k and taking the limit k → ∞, we obtain (31).

Property (33) easily follows from the fact that in the interval [0,∞), the scaled input flow function f_i^(k)(·) converges u.o.c. to the strictly increasing linear function f_i(0) + λ_i t. We omit details. █

Since some of the component functions included in x (viz.

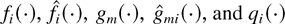
are Lipschitz in [0,∞), they are absolutely continuous. Therefore, at almost all points t ∈ [0,∞) (with respect to Lebesgue measure), the derivatives of all those functions exist. We will call such points regular.

In the rest of this article, when we consider a fixed limiting set of functions x, as defined in Lemma 1, we always assume that a sequence of prelimit paths {x^(k)}, which “defines it” (viz. the convergence properties of Lemma 1 hold), is fixed as well, along with the corresponding sequence of unscaled paths {X^(k)}.

5.2. Proof of Theorem 3 for the M-LWWF Discipline

The meaning of the following auxiliary lemma is that if relation (34) holds at some (scaled) time t, then by virtue of the M-LWWF scheduling rule, in some neighborhood of point t, flow i cannot be served.

Lemma 2: Consider the system with the M-LWWF discipline. With probability 1, a limiting set of functions x, as defined in Lemma 1, satisfies the following additional property. If

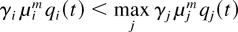
for some regular point t ≥ 0, for some i and m, then

Proof: Let us pick a j at which the maximum in inequality (34) is attained. In a similar manner to the proof of property (31) (in Lemma 1), we can fix a small positive δ₁ > 0 such that, for all sufficiently large k, for the unscaled path X^(k) we must have

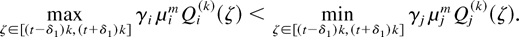
(If t = 0, then the time interval should be [0,δ₁ k] .) This means that in the interval [(t − δ₁)k + 1,(t + δ₁)k − 1] , queue i cannot be served in any time slot when the server is in state m because it would contradict the M-LWWF scheduling rule. Thus, for all sufficiently large k, we must have

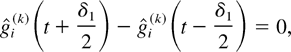
which implies

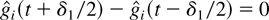
, and we are done. █

Let us introduce a quadratic Lyapunov function

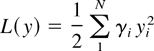
for a vector y = (y₁,…,y_N).

The following lemma embodies the key idea behind MaxWeight-type scheduling rules: They try to maximize the rate of decrease of the Lyapunov function L(q(t)). So, roughly speaking, since there exists at least one scheduling rule (e.g., an SSS rule with φ such that λ < v(φ)) under which L(q(t)) has a negative drift (when L(q(t)) > 0), the drift of L(q(t)) under M-LWWF has to be negative as well.

Lemma 3: Consider a system with the M-LWWF discipline. For any δ₁ > 0, there exists δ₂ > 0 such that the following holds. With probability 1, a limiting set of functions x, as defined in Lemma 1, satisfies the following additional properties:

L(q(t)),t ≥ 0, is an absolutely continuous function,

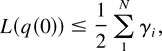
and at any regular point t,

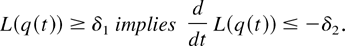
Proof: Let us pick a fixed stochastic matrix φ such that λ_i < v_i(φ) for all i. (The existence of such a matrix is condition (4).)

For any regular t ≥ 0 such that L(q(t)) > 0, the derivative of L(q(t)) can be written

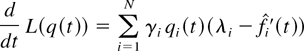
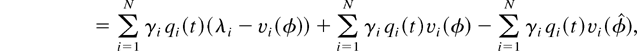
where

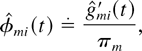
and we use the fact (following from property (31)) that

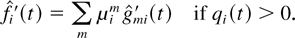
Let us choose δ₃ > 0 such that L(y) ≥ δ₁ implies max_i y_i ≥ δ₃. Then, the first sum in (40) is bounded as follows:

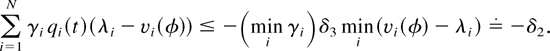
It remains to show that

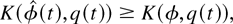
where K(ξ,y) denotes the function of a stochastic M × N matrix ξ and a nonnegative N-dimensional vector y, defined as

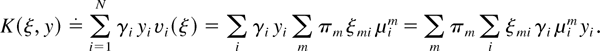
It is easy to see that for any nonnegative vector y, a stochastic matrix ξ maximizes K(ξ,y) if and only if the following condition holds for every i and m: If γ_i μ_i^my_i < max_j γ_j μ_j^my_j, then

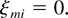
However, property (35) shows that (42) is satisfied for

. This proves (41) and the lemma. █

Lemma 4: Consider a system with the M-LWWF discipline. For any δ > 0, there exists T > 0 such that with probability 1, a limiting set of functions x, as defined in Lemma 1, satisfies the following additional property:

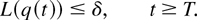
The proof follows from Lemma 3.

Proof of Theorem 3 for M-LWWF: According to Lemmas 1–4, for any fixed ε₁ > 0 we can always choose a large enough integer T > 0 such that for any sequence of random processes {X⁽ⁿ⁾}, there exists a subsequence {X^(k)} such that with probability 1, the convergence to a limiting set of functions x takes place and, moreover,

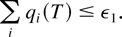
If we recall that T is large, then it follows from (44) that

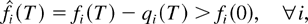
implying (by (33)) that

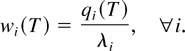
This, in turn, implies (since ε₁ is small) that

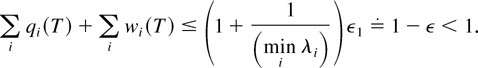
Therefore, with probability 1,

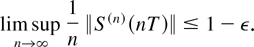
Since

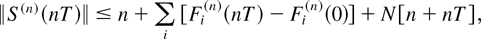
our input process assumptions easily imply that the sequence {(1/n)∥S⁽ⁿ⁾(nT)∥} is uniformly integrable. This, along with (47), verifies condition (10). The proof is complete. █

The following supplemental statement about the M-LWWF discipline will play an important role in the stability proof for the M-LWDF discipline.

Consider a generalized system with a given discipline H. The generalization is to assume that some time slots are unavailable for service of any queue. In each available for service time slot, the scheduling rule is H. In a generalized system, let G_m⁽ⁿ⁾(t) denote the number of available for service time slots (by time t) when the server is in state m. (Such a generalized system arises later, when we want to study the service dynamics of a subset of queues. To do that, we will view the time slots allocated to any other queue as unavailable for service of the subset of queues on which we focus.)

Lemma 5: Let positive constants K₀ and K₁ be fixed. Consider a sequence of fixed sample paths {X^(k)} of the generalized system under M-LWWF such that as k → ∞, all properties described in Lemmas 1 and 2 hold with the following modifications:

Property (22) is replaced by

property (26) is replaced by

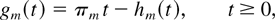
where each function h_m is nondecreasing Lipschitz-continuous, h_m(0) = 0, and

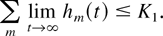
Then, the function L(q(t)) has the upper bound C < ∞, which depends only on K₀ and K₁:

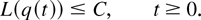
Proof: The idea of the proof is simple: the total “amount” of (scaled) time when service is unavailable to the queues is finite, bounded above by K₁. During the “rest of the time,” when the service is available, the Lyapunov function L(q(t)) cannot increase, due to the “reasons” presented in the proof of Lemma 3. However, we need to apply this idea in a continuous time setting, which requires some care with the estimates. We now proceed with the details.

We will use the notation L(t) [esdot ] L(q(t)). Let us choose δ > 0 small enough so that the following holds for regular points t. If g_m′(t) ≥ π_m − δ for each m, then (d/dt)L(t) < 0. (The existence of such a δ is easily obtained using the argument and the estimates used in the proof of Lemma 3.) Note that [sum ]_m h_m′(t) ≤ δ implies g_m′(t) ≥ π_m − δ for each m.

Let us denote by Λ the Lebesgue measure and by ℒ the σ-algebra of Lebesgue-measurable subsets of [0,∞). Consider the subset

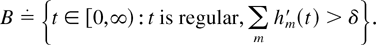
It is easy to check that B ∈ ℒ and

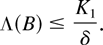
Define the measure ν on ℒ as follows:

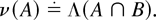
Notice that ν([0,∞)) = Λ(B).

For future reference, we note that for some fixed positive c₁ and c₂ and all regular t,

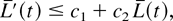
which follows from the estimate

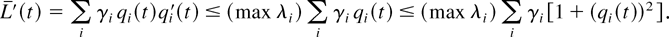
We see that the derivative L′(t) is bounded above as in (51) at regular points t ∈ B, and it is negative at regular points t ∈ [0,∞)[setmn ]B. We can write

Applying Gronwall's inequality [11, p.498], we obtain

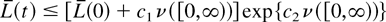
and, finally,

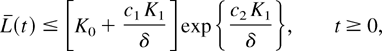
which proves the lemma. █

5.3. Proof of Theorem 3 for the M-LWDF Discipline

The following lemma describes the key property of the M-LWDF discipline which is analogous to the M-LWWF property described in Lemma 2.

Lemma 6: Consider a system with the M-LWDF discipline. With probability 1, a limiting set of functions x, as defined in Lemma 1, satisfies the following additional property. If in some interval [t₁,t₂], 0 ≤ t₁ < t₂ < ∞, for some fixed m and fixed i and j we have

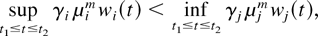
then

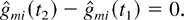
Proof: The proof is analogous to the proof of Lemma 2. (The only additional difficulty is the fact that the functions w_i(·) may not be continuous.) Note that condition (52) implies that μ_j^m > 0. We will consider only the nontrivial case when μ_i^m > 0. (The case μ_i^m = 0 is treated analogously to and simpler than this case.) Let us fix positive constants α and δ such that

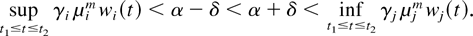
Then, for all t ∈ [t₁,t₂] , we have

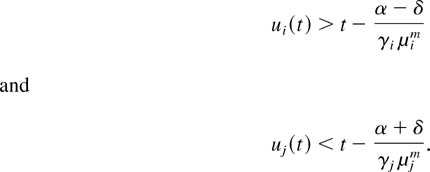
Since for each i, u_i(·) and all u_i^(k)(·) are nondecreasing and we have the convergence u_i^(k)(t) → u_i(t) for every t where u_i is continuous, we see that for all sufficiently large k and for all t ∈ [t₁,t₂] ,

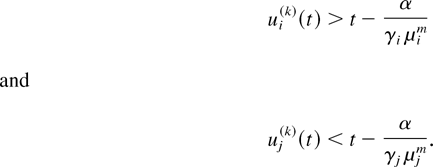
From the latter two inequalities, we see that

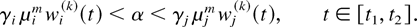
Just as in the proof of Lemma 2, we observe that the latter property implies that for all large k,

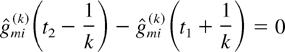
because the corresponding unscaled path X^(k) is such that queue i may not be served in any time slot in the interval [kt₁ + 1,kt₂ − 1] when the server is in state m. (Otherwise, we would get a violation of the M-LWDF scheduling rule.) Taking the limit k → ∞ completes the proof. █

The following lemma shows that under M-LWDF, all fluid limits x are such that after some fixed time T_N, all of the “initial fluid” is served (and, therefore, the linear relation q_i(t) = λ_i w_i(t) holds) for all t ≥ T_N and all queues i.

Lemma 7: Consider a system with the M-LWDF discipline. There exists T_N > 0 such that with probability 1, a limiting set of functions x, as defined in Lemma 1, satisfies the following additional property:

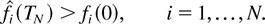
To illustrate the intuition behind the formal proof, we present the following informal discussion. Suppose we consider the system with two flows i = 1,2 and assume that by some fixed time T₁ ≥ 0, we have

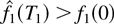
(i.e., all of the initial fluid of type 1 has been served). Consider a fixed sufficiently large time T₂. Let us show why the assumption that the initial type 2 fluid is not served by time T₂, namely

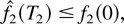
leads to a contradiction. We observe that, first, the flow 2 delay w₂(t) ≥ t for all t ∈ [T₁,T₂] . Second, the amount of time unavailable to flow 1 in [T₁,T₂] is bounded above: f₂(0) ≤ 1. Then, according to Lemma 5, q₁(t)—and therefore w₁(t) = q₁(t)/λ₁—is bounded above in [T₁,T₂] by a constant independent of T₂. Therefore, during most of the interval [T₁,T₂], the ratio of the waiting times w₂(t)/w₁(t) is very large. This means that (during most of the interval [T₁,T₂]) as long as the server state m is such that flow 2 can be served at strictly positive rate μ₂^m, the M-LWDF rule must choose for service queue 2 over queue 1. This means that the amount of time when queue 2 is served is of the order of T₂, which is large. However, then all of initial type 2 fluid, the amount of which is upper bounded by 1, must be served by time T₂—a contradiction to assumption (55).

Proof of Lemma 7: Let us fix an arbitrary ε₂ > 0. We have

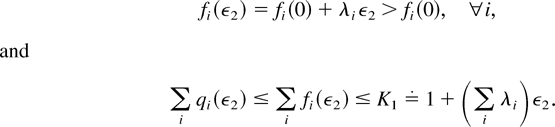
We will show the existence of T_N such that

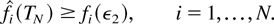
The proof of (56) is by induction.

Induction Base. There exists T₁ > 0 such that for at least one i,

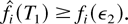
Let us set T₁ [esdot ] ε₂ + K₁ /π*, where π* is the sum of the stationary probabilities π_m over server states m such that μ_j^m > 0 for at least one j. Suppose the statement of the induction base, with this T₁, does not hold. Then, for all sufficiently large k, we must have

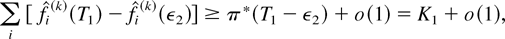
where o(1) is a term vanishing as k → ∞. Taking the k → ∞ limit, we obtain

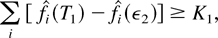
which means (see the definition of K₁) that

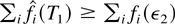
and, therefore,

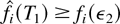
for at least one i. This contradiction proves the induction base.

Induction Step. Suppose that there exists T_l > 0, 1 ≤ l < N such that for at least one subset N_l ⊂ {1,…,N} of cardinality l, we have

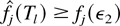
for all j ∈ N_l. Then, there exists T_l+1 ≥ T_l such that (57) holds for all j within at least one subset N_l+1 of cardinality l + 1.

We will prove the induction step for l = 1. (The generalization for arbitrary l is straightforward.) Thus, we need to prove the existence of T₂ ≥ T₁ such that for at least two different flows i and r, (57) holds for j = i,r, with T₁ being the constant from the induction base statement.

Let us fix i for which

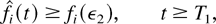
according to the induction base. Suppose

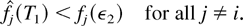
We observe that

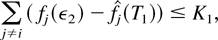
where K₁ is as defined earlier, and

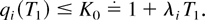
Suppose that a constant T₂ > T₁ is fixed such that

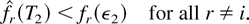
(Below, we provide a choice of T₂ such that assumption (59) leads to a contradiction.)

Let us view each unscaled path X^(k) after time kT₁ as a generalized system (described just above Lemma 5) with the single input flow of type i and with time slots allocated to any other flow being unavailable to flow i. (By convention, only the slots in which at least one customer of at least one flow r ≠ i was actually served are considered unavailable to flow i.) Then, for the scaled generalized system, starting at time T₁, we have

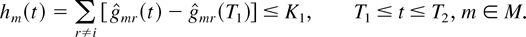
Since x is such that the simple linear relation λ_i w_i(t) = q_i(t) holds for flow i for all t ≥ T₁, the generalized system with the M-LWDF discipline satisfies all of the properties of the generalized system with the M-LWWF discipline (including Lemma 5), with each γ_i replaced by γ_i /λ_i. Thus, from Lemma 5, we have

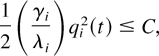
where the left-hand side is the “L(q(t))” for the generalized system and C ≥ 0 is the constant defined in Lemma 5, depending only on the constants K₀ and K₁ specified in this proof. From the last display we have the estimate

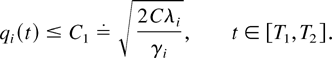
Note that C₁ does not depend on the choice of T₂.

From this point, we “switch back” to interpreting X^(k) as a path of the original system. Let us denote by M(i) the subset of elements m ∈ M such that μ_j^m > 0 for at least one flow j ≠ i and denote π*(i) [esdot ] [sum ]_m∈M(i) π_m. Let us choose T₂′ > T₁ large enough so that for any pair of j ≠ i and m ∈ M such that μ_j^m > 0, we have

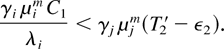
Finally, let us choose T₂ > T₂′ large enough so that

Our choice of T₂′ in (62) guarantees that for all sufficiently large k, the unscaled path X^(k) must be (according to the M-LWDF rule) such that in the interval [kT₂′,kT₂] , in every time slot in which the state of the server belongs to the set M(i), one of the flows r ≠ i is chosen for service. This observation implies that in the k → ∞ limit for the corresponding scaled paths, we must have

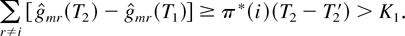
This is a contradiction to (60), which shows that, for the T₂ chosen above, (59) cannot hold, and, therefore,

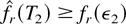
for at least one r ≠ i.

We have proved claim (63), assuming condition (58). However, the opposite of condition (58) means that, trivially, (63) holds for some r ≠ i and any T₂ ≥ T₁. Thus, (63) holds for the chosen T₂ regardless of condition (58).

Our choice of T₂ depended on i. However, since there is only a finite number of possible values of i, we can choose T₂ so that (63) holds for some r ≠ i no matter what i is. The proof of the induction step is complete. █

Proof of Theorem 3 for M-LWDF: We proved the existence of T_N > 0 such that for any sequence of random processes {X⁽ⁿ⁾}, there exists a subsequence {X^(k)} such that with probability 1, the convergence to a limiting set of functions x takes place, and, moreover, x is such that the linear relation exists for all i:

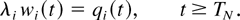
This fact, along with Lemma 6, means that with probability 1 in the interval [T_N,∞) the set x also satisfies all the properties described in Lemmas 2–4 if only in their formulations we replace γ_i by γ_i /λ_i, replace (37) by the condition

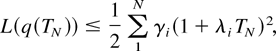
and move the time origin to T_N. Therefore, for any ε₁ > 0, there exists T ≥ T_N such that with probability 1, x satisfies the condition

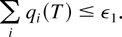
The rest is exactly as in the proof of the theorem for M-LWWF. The only difference is that we obtain (46) directly from the property (33) and Lemma 7, not from (45).

6. CONCLUSIONS

We consider the variable channel scheduling queuing model which naturally arises in wireless communications. We show that a wide class of online scheduling rules, including the M-LWDF and M-LWWF rules (and their generalizations), are throughput optimal (i.e., they make all queues stable as long as the flow arrival rates are within the system stability region). One of the main contributions of this work is that we show that the throughput optimality of MaxWeight-type scheduling rules is preserved when flow waiting times are used as queue state variables in place of (or in conjunction with) the queue lengths.

We believe that the class of scheduling algorithms we study in this article can be efficiently used in applications to provide flexible control of quality of service to multiple data flows—in particular flows sharing a time-varying wireless link.

Acknowledgment

We would like to thank Sem Borst for numerous useful discussions.

APPENDIX: Details of the Proof of Sufficiency in Theorem 1

Lemma 1 holds for any scheduling rule, including the SSS rule associated with the matrix φ. For this rule, with probability 1, a limiting set of functions x is such that

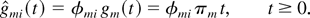
From this and the argument analogous to that used in (39) and (40), we see that at any regular point t ≥ 0, condition q_i(t) > 0 implies

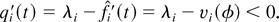
Therefore, q(t) ≡ 0 for all t ≥ max_i 1/(v_i(φ) − λ_i). The rest of the proof is the same as in the proof of Theorem 3 for the M-LWWF rule, which follows Lemma 4 in Section 5.2. █