Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T10:13:24.736Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic comparison of parallel systems with Pareto components

Part of: Distribution theory - Probability Sampling theory, sample surveys Survival analysis and censored data Nonparametric inference

Published online by Cambridge University Press:  20 May 2021

Sameen Naqvi Open the ORCID record for Sameen Naqvi [Opens in a new window] ,
Weiyong Ding  and
Peng Zhao Open the ORCID record for Peng Zhao [Opens in a new window]
Sameen Naqvi
Affiliation:
Department of Mathematics, Indian Institute of Technology Hyderabad, Kandi 502285, India. E-mail: sameen@math.iith.ac.in
Weiyong Ding
Affiliation:
School of Mathematics and Statistics, Jiangsu Normal University, Xuzhou 22116, China. E-mail: mathdwy@hotmail.com, zhaop@jsnu.edu.cn
Peng Zhao
Affiliation:
School of Mathematics and Statistics, Jiangsu Normal University, Xuzhou 22116, China. E-mail: mathdwy@hotmail.com, zhaop@jsnu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Pareto distribution is an important distribution in extreme value theory. In this paper, we consider parallel systems with Pareto components and study the effect of heterogeneity on skewness of such systems. It is shown that, when the lifetimes of components have different shape parameters, the parallel system with heterogeneous Pareto component lifetimes is more skewed than the system with independent and identically distributed Pareto components. However, for the case when the lifetimes of components have different scale parameters, the result gets reversed in the sense of star ordering. We also establish the relation between star ordering and dispersive ordering by extending the result of Deshpande and Kochar [(1983). Dispersive ordering is the same as tail ordering. Advances in Applied Probability 15(3): 686–687] from support 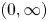$(0, \infty )$ to general supports 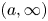$(a, \infty )$, 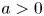$a > 0$. As a consequence, we obtain some new results on dispersion of order statistics from heterogeneous Pareto samples with respect to dispersive ordering.

Keywords

Convex transform orderDispersive orderParallel systemPareto distributionStar order

MSC classification

Primary: 60E15: Inequalities; stochastic orderings
Secondary: 62N05: Reliability and life testing 62G30: Order statistics; empirical distribution functions 62D05: Sampling theory, sample surveys
Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 36 , Issue 4 , October 2022 , pp. 950 - 962
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdel-All, N.H. & Abd-Ellah, H.N. (2016). Geometric visualization of parallel bivariate Pareto distribution surfaces. Journal of the Egyptian Mathematical Society 24(2): 250–257.CrossRefGoogle Scholar
Barlow, R.E. & Proschan, F (1975). Statistical theory of reliability and life testing: probability models. Florida, USA: Florida State University Tallahassee.Google Scholar
Da, G., Xu, M., & Balakrishnan, N. (2014). On the Lorenz ordering of order statistics from exponential populations and some applications. Journal of Multivariate Analysis 127: 88–97.CrossRefGoogle Scholar
Deshpande, J.V. & Kochar, S.C. (1983). Dispersive ordering is the same as tail-ordering. Advances in Applied Probability 15(3): 686–687.CrossRefGoogle Scholar
Ding, W., Yang, J., & Ling, X. (2017). On the skewness of extreme order statistics from heterogeneous samples. Communications in Statistics – Theory and Methods 46(5): 2315–2331.CrossRefGoogle Scholar
Fang, R. & Li, X. (2018). Ordering extremes of interdependent random variables. Communications in Statistics – Theory and Methods 47(17): 4187–4201.CrossRefGoogle Scholar
Fang, L. & Zhang, X. (2013). Stochastic comparisons of series systems with heterogeneous Weibull components. Statistics & Probability Letters 83(7): 1649–1653.CrossRefGoogle Scholar
Fang, R., Li, C., & Li, X. (2018). Ordering results on extremes of scaled random variables with dependent and proportional hazards. Statistics 52(2): 458–478.CrossRefGoogle Scholar
Hu, T. & Wang, Y. (2009). Optimal allocation of active redundancies in r-out-of-n systems. Journal of Statistical Planning and Inference 139(10): 3733–3737.CrossRefGoogle Scholar
Khaledi, B.E. & Kochar, S. (2000). Some new results on stochastic comparisons of parallel systems. Journal of Applied Probability 37(4): 1123–1128.CrossRefGoogle Scholar
Khaledi, B.E. & Kochar, S. (2002). Stochastic orderings among order statistics and sample spacings. In Uncertainty and optimality: probability, statistics and operations research, Singapore: World Scientific Publications, pp. 167–203.CrossRefGoogle Scholar
Kochar, S.C. & Xu, M. (2007). Some recent results on stochastic comparisons and dependence among order statistics in the case of PHR model. Journal of Reliability and Statistical Studies 6: 125–140.Google Scholar
Kochar, S. & Xu, M. (2007). Stochastic comparisons of parallel systems when components have proportional hazard rates. Probability in the Engineering and Informational Sciences 21(4): 597–609.CrossRefGoogle Scholar
Kochar, S. & Xu, M. (2009). Comparisons of parallel systems according to the convex transform order. Journal of Applied Probability 46(2): 342–352.CrossRefGoogle Scholar
Kochar, S. & Xu, M. (2014). On the skewness of order statistics with applications. Annals of Operations Research 212(1): 127–138.CrossRefGoogle Scholar
Marshall, A.W. & Olkin, I (2007). Life distributions, vol. 13. New York: Springer.Google Scholar
Mitrinovic, D.S. & Vasic, P.M (1970). Analytic inequalities, vol. 1. Berlin: Springer-verlag.CrossRefGoogle Scholar
Nadarajah, S., Jiang, X., & Chu, J. (2017). Comparisons of smallest order statistics from Pareto distributions with different scale and shape parameters. Annals of Operations Research 254(1): 191–209.CrossRefGoogle Scholar
Oja, H. (1981). On location, scale, skewness and kurtosis of univariate distributions. Scandinavian Journal of Statistics 8: 154–168.Google Scholar
Shaked, M. & Shanthikumar, J.G (2007). Stochastic orders. New York, USA: Springer Science & Business Media.CrossRefGoogle Scholar
van Zwet, W.R (1964). Mathematical centre tracts: vol. 7. Convex transformations of random variables. Amsterdam: Mathematical Centre.Google Scholar
Zhao, P., Chan, P.S., & Ng, H.K.T. (2012). Optimal allocation of redundancies in series systems. European Journal of Operational Research 220(3): 673–683.CrossRefGoogle Scholar