Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Starreveld, Nicos
Bekker, Réne
and
Mandjes, Michel
2018.
Occupation times of alternating renewal processes with Lévy applications.
Journal of Applied Probability,
Vol. 55,
Issue. 4,
p.
1287.

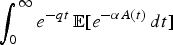 can be computed. It turns out that these follow, for given nonnegative α and
can be computed. It turns out that these follow, for given nonnegative α and 