Published online by Cambridge University Press: 29 November 2018
In this paper, we consider the existence of multiple solutions for the quasilinear Schrödinger equation 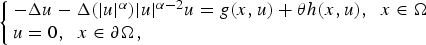 $$\left\{ {\matrix{ {-\Delta u-\Delta (\vert u \vert ^\alpha )\vert u \vert ^{\alpha -2}u = g(x,u) + \theta h(x,u),\;\;x\in \Omega } \hfill \cr {u = 0,\;\;x\in \partial \Omega ,} \hfill \cr } } \right.$$
$$\left\{ {\matrix{ {-\Delta u-\Delta (\vert u \vert ^\alpha )\vert u \vert ^{\alpha -2}u = g(x,u) + \theta h(x,u),\;\;x\in \Omega } \hfill \cr {u = 0,\;\;x\in \partial \Omega ,} \hfill \cr } } \right.$$