No CrossRef data available.
Published online by Cambridge University Press: 11 November 2020
We consider the adjoint representation of a Hopf algebra $H$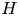 focusing on the locally finite part, $H_{{\textrm ad\,fin}}$
focusing on the locally finite part, $H_{{\textrm ad\,fin}}$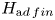 , defined as the sum of all finite-dimensional subrepresentations. For virtually cocommutative $H$
, defined as the sum of all finite-dimensional subrepresentations. For virtually cocommutative $H$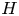 (i.e., $H$
(i.e., $H$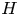 is finitely generated as module over a cocommutative Hopf subalgebra), we show that $H_{{\textrm ad\,fin}}$
is finitely generated as module over a cocommutative Hopf subalgebra), we show that $H_{{\textrm ad\,fin}}$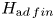 is a Hopf subalgebra of $H$
is a Hopf subalgebra of $H$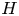 . This is a consequence of the fact, proved here, that locally finite parts yield a tensor functor on the module category of any virtually pointed Hopf algebra. For general Hopf algebras, $H_{{\textrm ad\,fin}}$
. This is a consequence of the fact, proved here, that locally finite parts yield a tensor functor on the module category of any virtually pointed Hopf algebra. For general Hopf algebras, $H_{{\textrm ad\,fin}}$ is shown to be a left coideal subalgebra. We also prove a version of Dietzmann's Lemma from group theory for Hopf algebras.
is shown to be a left coideal subalgebra. We also prove a version of Dietzmann's Lemma from group theory for Hopf algebras.